Der Dijkstra Algorithmus gehört zur Gruppe der Greedy Algorithmen. Er dient der Berechnung des kürzesten Pfades in einem Graphen von einem gegebenen Startpunkt aus.
Dieses Kapitel zeigt dir, warum der Dijkstra Algorithmus wichtig ist und was man unter ihm versteht. Außerdem zeigen wir dir, wie du den Dijkstra Algorithmus anwendest und stellen dir am Ende einige Übungsaufgaben zur Verfügung, die dich bei der Prüfungsvorbereitung unterstützen können.
Warum ist der Dijkstra Algorithmus wichtig?
Zur Lösung von Optimierungsproblemen im Rahmen des Operations Research im Betrieb werden häufig Algorithmen verwendet. Einer von ihnen ist der „Dijkstra Algorithmus“, welcher zur Gruppe der Greedy Algorithmen gehört.
Mithilfe dieses Algorithmus ist es möglich, den kostengünstigsten bzw. kürzesten Weg in einem Graphen zu berechnen. Dazu werden die Kantengewichte des Graphen betrachtet, welche die Kosten für den Weg von einem Knoten zum nächsten beschreiben. Der Dijkstra Algorithmus wird beispielsweise in Routenplanern und Navigationsgeräten eingesetzt
Was versteht man unter dem Dijkstra Algorithmus?
Der nach seinem Erfinder Edsger W. Dijkstra benannte Dijkstra Algorithmus ist eine Methode zur Lösung von Optimierungsproblemen, bei denen nach dem kostengünstigsten oder kürzesten Pfad in einem Graphen gesucht wird.
Grundvoraussetzung zur Anwendung des Dijkstra Algorithmus ist, dass die Kantengewichte innerhalb des zu untersuchenden Graphen nicht negativ sind. Sind negative Kantengewichte vorhanden, eignet sich der „Bellman-Ford-Algorithmus“ besser zur Lösung des Problems.
Beispiel: Anwendung des Dijkstra Algorithmus
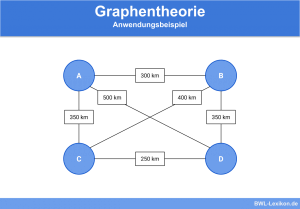
Um seine Reiseroute zu planen, stellt er folgenden Graph auf, der die möglichen Reisewege und die Entfernungen der einzelnen Knotenpunkte zueinander darstellt:
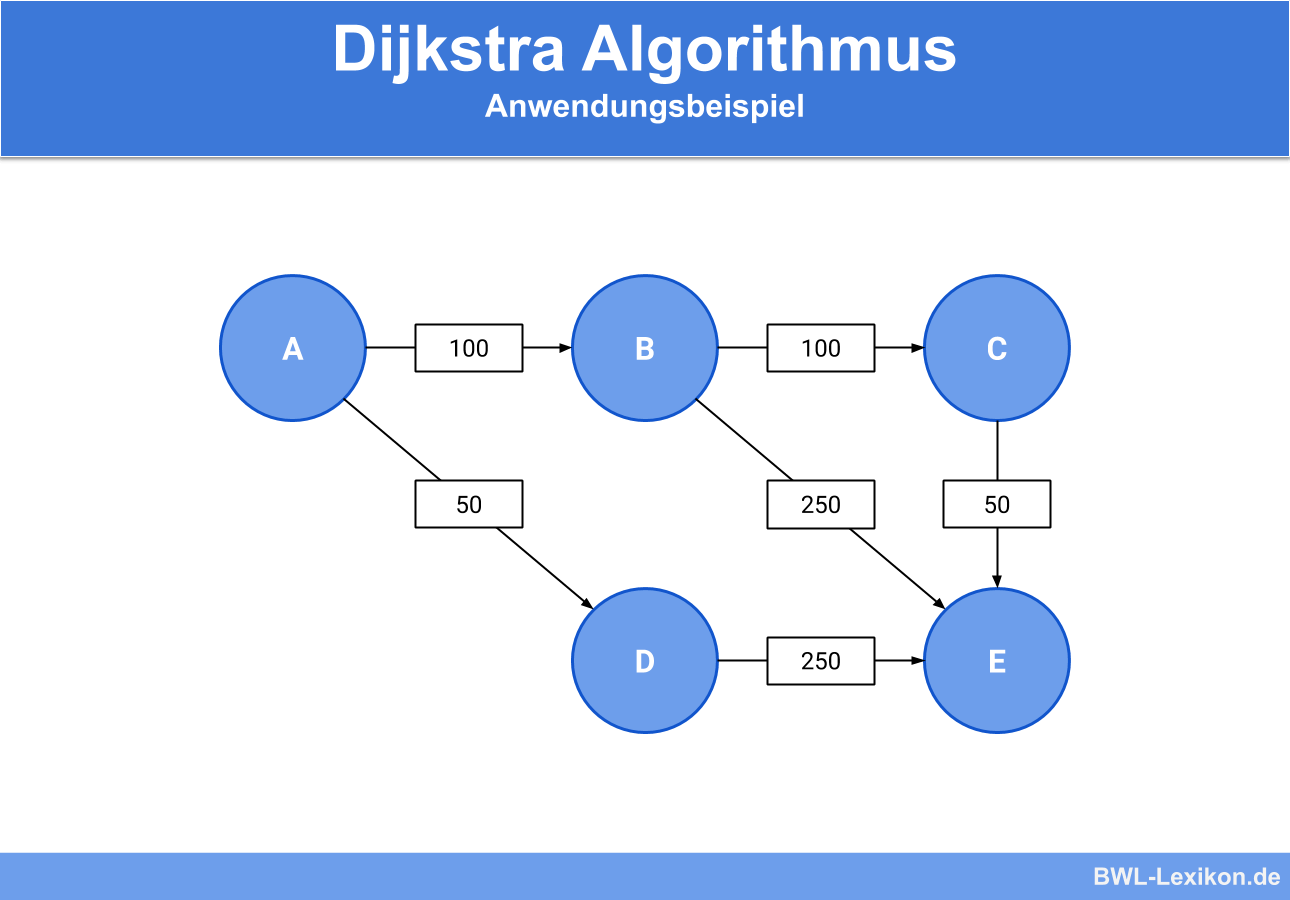
Damit die kürzeste Route von Stadt A nach Stadt E gefunden werden kann, wird nun der Dijkstra Algorithmus angewendet:
1. Schritt: Initialisierung des Algorithmus
Um den Algorithmus zu initialisieren, wird eine Tabelle angelegt. Zu Beginn betragen die Kosten Null, da am Startpunkt begonnen wird. Der Weg zu den weiteren Knoten ist noch nicht bekannt, daher nehmen wir für die Kosten vorerst „unendlich“ an.
In der Warteschlange befinden sich alle Knoten, die wir bereits gefunden haben. Zu Beginn ist das lediglich der Startpunkt A. Einen Vorgänger des Startpunktes gibt es nicht. Die gefüllte Tabelle sieht dann also folgendermaßen aus:
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 |
2. Schritt: 1. Iteration
Nach der Initialisierung des Algorithmus kann mit der ersten Iteration begonnen werden. In der Warteschlange aus dem vorherigen Schritt befindet sich der Knoten A. Daher wird dieser nun ausgewählt. Betrachtet werden dessen direkte Nachfolger, die Knoten B und D.
Die Entfernung von A nach B beträgt 100, die von A nach D 50. Diese stellen die Kosten dar. Da die beiden Nachfolger des Startpunktes nun betrachtet wurden, gilt dieser als erledigt. In der Warteschlange stehen nun B und D.
Mögliche Nachfolger der betrachteten Knoten sind C und E. Die Tabelle sieht dementsprechend folgendermaßen aus:
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | Kosten: Vorgänger: | 0 - | 100 A | ∞ - | 50 A | ∞ - | Warteschlange: B,D Erledigt: A Ausgewählt: B, D Nachfolger: C,E |
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 |
3. Schritt: 2. Iteration
Es folgt nun die 2. Iteration. Hierzu wird der Knoten aus der Warteschlange ausgewählt, welcher die geringsten Kosten aufweist, also Knoten D. Der Nachfolger dieses Knotens, Knoten E, wird nun betrachtet.
Die Kosten, um zum Knoten E zu gelangen, betragen 300. Da Knoten D nun betrachtet wurde, kann dieser aus der Warteschlange genommen und als erledigt markiert werden. Knoten B bleibt in der Warteschlange und wird um Knoten E ergänzt.
Die Tabelle gestaltet sich dann folgendermaßen:
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | Kosten: Vorgänger: | 0 - | 100 A | ∞ - | 50 A | ∞ - | Warteschlange: B,D Erledigt: A Ausgewählt: B, D Nachfolger: C,E |
| 2 | Kosten: Vorgänger: | 0 - | 100 A | 50 A | ∞ - | 300 D | Warteschlange: B,E Erledigt: A, D Ausgewählt: D Nachfolger: C,E |
| 3 | |||||||
| 4 | |||||||
| 5 |
4. Schritt: 3. Iteration
Auch bei der dritten Iteration wird nach dem gleichen Schema vorgegangen. Wir schauen uns nun die Kosten für den Knoten C an. Diese betragen 200. Sein direkter Vorgänger ist Knoten B. Wir können B damit als erledigt markieren und C zusätzlich in die Warteschlange aufnehmen.
Diese Informationen werden in der Tabelle ergänzt:
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | Kosten: Vorgänger: | 0 - | 100 A | ∞ - | 50 A | ∞ - | Warteschlange: B,D Erledigt: A Ausgewählt: B, D Nachfolger: C,E |
| 2 | Kosten: Vorgänger: | 0 - | 100 A | 50 A | ∞ - | 300 D | Warteschlange: B,E Erledigt: A, D Ausgewählt: D Nachfolger: C,E |
| 3 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 300 D | Warteschlange: C,E Erledigt: A, D, B Ausgewählt: C Nachfolger: E |
| 4 | |||||||
| 5 |
5. Schritt: 4. Iteration
Betrachten wir nun den Nachfolger von Knoten C. Dies ist Knoten E. Aktuell betragen die Kosten für E 300. Wenn wir aber den Weg über Knoten B und C wählen, betragen die neuen Kosten für E nur noch 250 mit dem neuen Vorgänger C. Damit ist auch Knoten E erledigt. Es gibt keine weiteren Nachfolger.
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | Kosten: Vorgänger: | 0 - | 100 A | ∞ - | 50 A | ∞ - | Warteschlange: B,D Erledigt: A Ausgewählt: B, D Nachfolger: C,E |
| 2 | Kosten: Vorgänger: | 0 - | 100 A | 50 A | ∞ - | 300 D | Warteschlange: B,E Erledigt: A, D Ausgewählt: D Nachfolger: C,E |
| 3 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 300 D | Warteschlange: C,E Erledigt: A, D, B Ausgewählt: C Nachfolger: E |
| 4 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 250 C | Warteschlange: E Erledigt: A, B, C, D Ausgewählt: E Nachfolger: - |
| 5 |
6. Schritt: 5. Iteration
In der letzten Iteration stellen wir fest, dass alle Knoten erledigt sind, da wir keinen Knoten mehr in die Warteschlange aufnehmen können. Wir können unseren Algorithmus an dieser Stelle also beenden.
| Iteration | A | B | C | D | E | ||
|---|---|---|---|---|---|---|---|
| 0 | Kosten: Vorgänger: | 0 - | ∞ - | ∞ - | ∞ - | ∞ - | Warteschlange: A Erledigt: - Ausgewählt: A Nachfolger: B, D |
| 1 | Kosten: Vorgänger: | 0 - | 100 A | ∞ - | 50 A | ∞ - | Warteschlange: B,D Erledigt: A Ausgewählt: B, D Nachfolger: C,E |
| 2 | Kosten: Vorgänger: | 0 - | 100 A | 50 A | ∞ - | 300 D | Warteschlange: B,E Erledigt: A, D Ausgewählt: D Nachfolger: C,E |
| 3 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 300 D | Warteschlange: C,E Erledigt: A, D, B Ausgewählt: C Nachfolger: E |
| 4 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 250 C | Warteschlange: E Erledigt: A, B, C, D Ausgewählt: E Nachfolger: - |
| 5 | Kosten: Vorgänger: | 0 - | 100 A | 200 B | 50 A | 250 C | Warteschlange: - Erledigt: A, B, C, D, E Ausgewählt: - Nachfolger: - |
Anhand der vollständigen Tabelle können wir nun den günstigsten Weg vom Startpunkt A zum Endpunkt E ablesen. Dazu betrachten wir die Tabelle rekursiv. Das bedeutet, wir starten die Betrachtung beim Knoten E. Dieser hat Gesamtkosten von 250. Sein Vorgänger ist Knoten C. Der Vorgänger von Knoten C ist Knoten B, welcher nach Knoten A folgt.
Der kürzeste Weg zum Knoten E ist also der Weg von A über B nach C zu E mit Gesamtkosten von 250.