Graphentheorie

Die Graphentheorie als mathematische Methode befasst sich mit der Untersuchung von Graphen als Darstellung von einer Vielzahl von Problemen. Insbesondere in der Logistik und dem Projektmanagement kommen die praktischen Anwendungsmöglichkeiten der Graphentheorie zum Zuge.

In diesem Kapitel erfährst du, warum die Graphentheorie wichtig ist und was sie ausmacht. Anhand der nachfolgenden Übungsaufgaben kannst du dein Wissen testen und dich auf deine nächste Prüfung vorbereiten.

Warum ist die Graphentheorie wichtig?

Als Teilgebiet der Mathematik untersucht die Graphentheorie die Eigenschaften von Graphen und deren Beziehungen zueinander. Was auf den ersten Blick als abstrakte und stark theoretische Betrachtung erscheint, kann tatsächlich Lösungsansätze für eine Vielzahl von alltäglichen und betriebsrelevanten Problemen liefern.

Neben den Wirtschaftswissenschaften findet die Graphentheorie auch in der Informatik Anwendung, da sich eine Vielzahl von algorithmischen Problemen mittels Graphentheorie lösen lassen.

Was versteht man unter der Graphentheorie?

Ein “Graph G” besteht grundsätzlich aus folgenden Bestandteilen:

• Menge an Knoten V
• Menge an Kanten E

Zwei Knoten werden dabei immer von einer Kante verbunden. Dabei kann man unterschiedliche Arten von Graphen unterscheiden.

Unterscheidungen bei Graphen

Grundsätzlich kann zwischen gerichteten und ungerichteten Graphen unterschieden werden. Dabei unterscheiden sich die Graphen in der Eigenschaft der jeweiligen Kanten zwischen den Knoten.

Gerichtete und ungerichtete Graphen

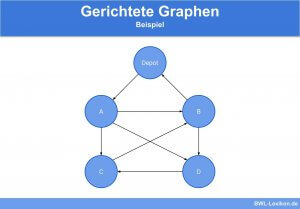
• Gerichtete Graphen:
  Die Kanten, welche die einzelnen Knoten verbinden, sind als Pfeil dargestellt. Somit kann die Kante nur in entsprechend der Pfeilrichtung genutzt werden.
• Ungerichtete Graphen:
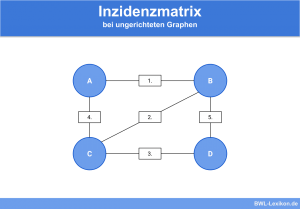
  Hierbei können die Kanten des Graphen als Verbindung zwischen den Knoten in beide Richtungen genutzt werden.

Zusammenhängende und nicht zusammenhängende Graphen

Neben der Unterscheidung zwischen gerichteten und ungerichteten Graphen ist auch der Zusammenhang des Graphen zu betrachten:

• zusammenhängende Graphen:
  Von jedem Knotenpaar aus ist jeder beliebige Knoten erreichbar. Als schwach zusammenhängend bezeichnet man einen Graphen, bei dem durch die Richtung der Kanten ein Knotenpunkt nicht erreichbar ist. Können alle Knoten auch unter Beachtung der Richtungen der Kanten erreicht werden, spricht man von einem stark zusammenhängenden Graphen.
• nicht zusammenhängende Graphen:
  Verfügt der Graph über isolierte Knoten oder Knotengruppen, ist also nicht jeder Knoten erreichbar, so handelt es sich um einen nicht zusammenhängenden Graphen.

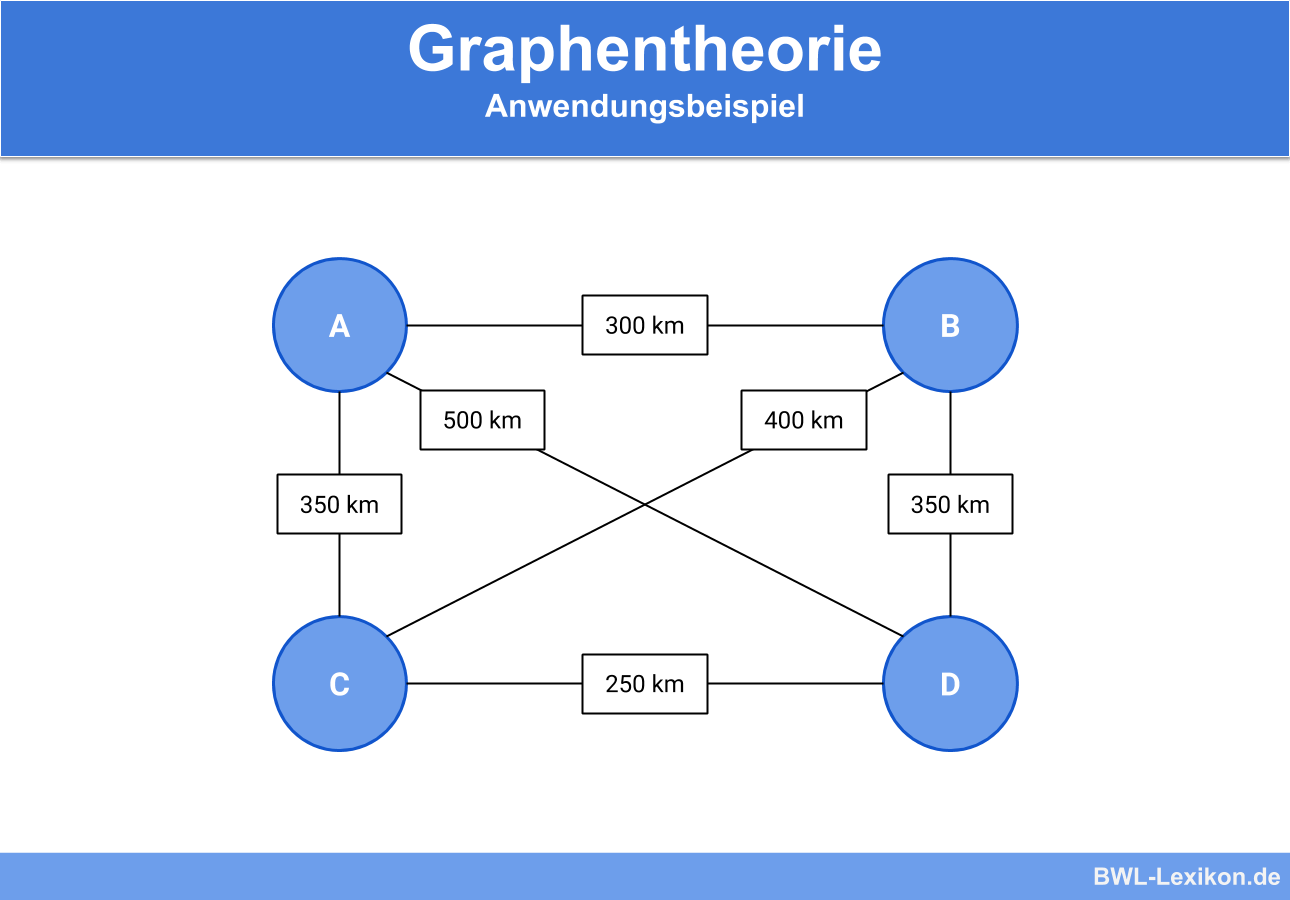
Gewichteten und ungewichteten Graphen

Ein weiterer Unterschied besteht in gewichteten und ungewichteten Graphen:

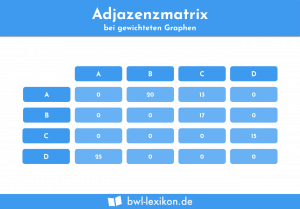
• gewichtete Graphen:
  Die Längen der einzelnen Kanten sind unterschiedlich und müssen berücksichtigt werden.
• ungewichtete Graphen:
  Die Kantenlängen zwischen den Knotenpunkten sind gleich lang oder die Länge spielt keine Rolle in der Betrachtung.

Knotengrad bei Graphen

Der Knotengrad gibt die Anzahl der ein- bzw. ausgehenden Kanten an einem Knotenpunkt an. Auch hierbei unterscheidet man zwischen gerichteten und ungerichteten Graphen.

Knotengrad bei gerichteten Graphen

Bei gerichteten Graphen, also denjenigen, deren Kanten nur bestimmte Richtungen erlauben, ist zwischen dem Eingangsgrad und dem Ausgangsgrad zu unterscheiden. Der Eingangsgrad bezeichnet dabei die Anzahl der eingehenden Kanten, der Ausgangsgrad die Anzahl der ausgehenden Kanten.

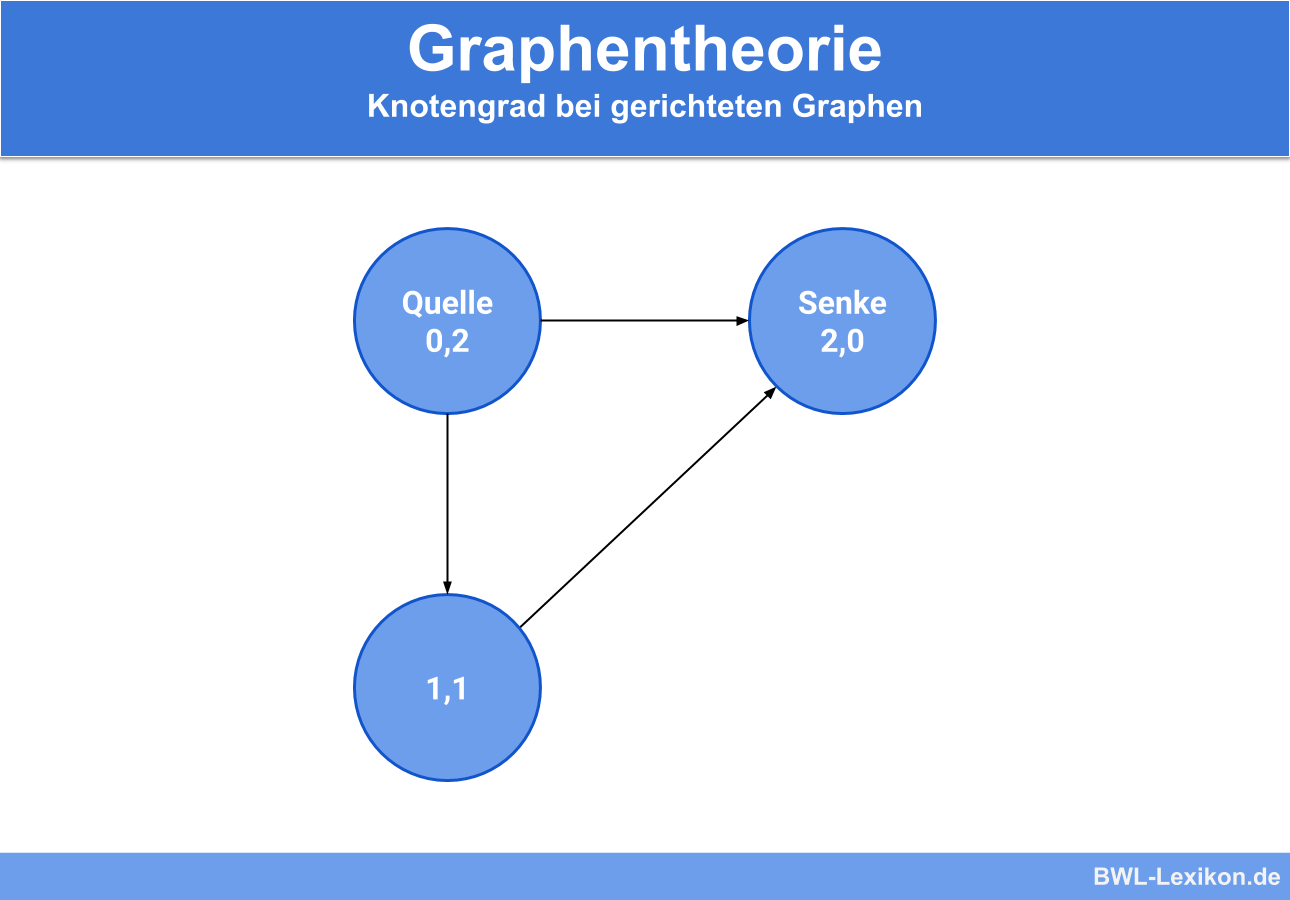
Der Eingangsgrad wird dabei als erstes genannt, als zweites der Ausgangsgrad. Besitzt ein Knoten keine eingehenden Kanten sondern nur ausgehende, so wird dieser als Quelle bezeichnet. Knoten, die keine ausgehenden Kanten und nur eingehende aufweisen, nennt man Senke.

Ein gerichteter Graph mit Angabe des Knotengrades könnte folgendermaßen aussehen:

Knotengrad bei ungerichteten Graphen

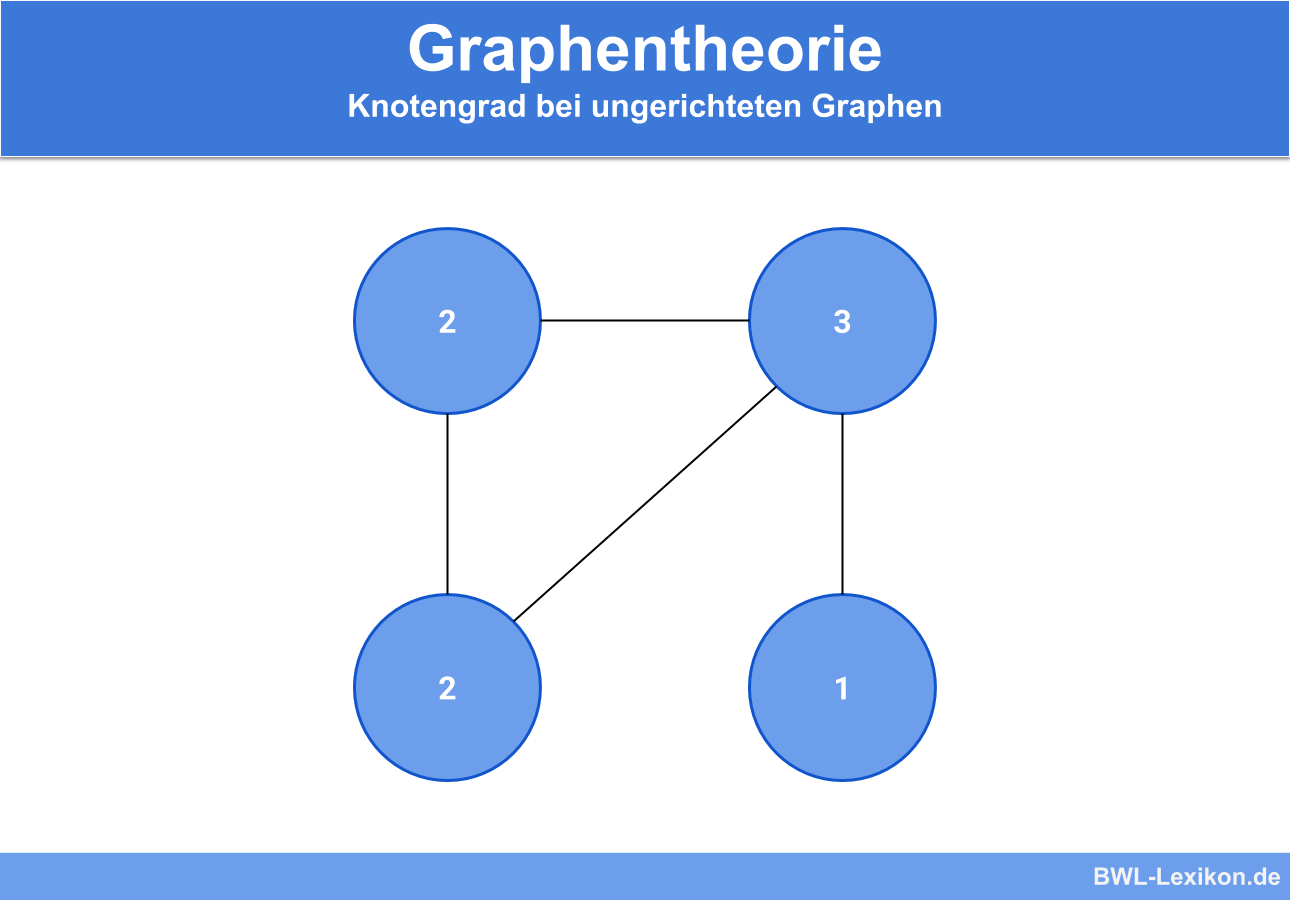
Bei ungerichteten Graphen spielt die Richtung der Kanten keine Rolle. Daher wird auch nicht zwischen Eingangs- und Ausgangsgrad unterschieden. Der Knotengrad gibt daher die Anzahl aller an den Knotenpunkt anschließenden Kanten an. Die Knoten werden daher auch als benachbarte Knoten bezeichnet.

Dies könnte folgendermaßen aussehen:

Anwendung der Graphentheorie

Die Erkenntnisse der Graphentheorie können für eine Vielzahl von Problemlösungen genutzt werden. Ein typisches Beispiel ist das bekannte “Problem des Handlungsreisenden”.

Beispiel

Der Vertreter der “Glasklar AG” möchte in verschiedenen Städten mögliche neue Kunden besuchen, um Vertragsabschlüsse zu künftigen Geschäftsbeziehungen vorzubereiten. Dabei soll die möglichst effektivste Route gefunden werden – unter der Bedingung, dass jeder Ort nur einmal besucht werden darf und er am Ende wieder in seiner Heimatstadt ankommt. Als Graph dargestellt könnte dies folgendermaßen aussehen:

Zur Lösung dieses Problems stehen unterschiedliche Methoden zur Verfügung, insbesondere Algorithmen, die es erlauben unter möglichst wenig Aufwand die bestmögliche Route zu finden.

Diese sind beispielsweise:

• der Greedy Algorithmus
• der Dijkstra Algorithmus
• der Kruskal Algorithmus
• der Prim Algorithmus
• der Bellmann Ford Algorithmus
• die Ungarische Methode.

Übungsfragen

 

#1. Was versteht man unter der Graphentheorie?

Die Graphentheorie beschreibt das Verhalten verschiedener Marktteilnehmer, die sich wie mittelalterliche Grafschaften verhalten.

Die Graphentheorie ist eine mathematische Methode, mit der unterschiedlichste Probleme abstrakt in Form von Graphen dargestellt werden können, um so mit Hilfe von Algorithmen die bestmögliche Lösung zu ermitteln.

Die Graphentheorie ist eine mathematische Methode, mit der die Graphen von Funktionen, beispielsweise der Gewinnentwicklung interpretiert werden können.

#2. Welche Elemente sind Bestandteil eines Graphen in der Graphentheorie?

Der Menge an Netzknoten und der Menge an Pufferzeiten.

Der Menge an Graphen und gerichteten Kanten.

Der Menge an Knotenpunkten und der Menge an Kanten zwischen den Knotenpunkten.

#3. Was ist der Unterschied zwischen gerichteten und ungerichteten Graphen?

Gerichtete Kanten können nur in eine Richtung genutzt werden, ungerichtete in beide Richtungen.

Gerichtete Kanten können nicht genutzt werden, ungerichtete hingegen schon.

Gerichtete Kanten haben immer eine bestimmte Länge, ungerichtete nicht.

#4. “In der Graphentheorie kann zwischen gewichteten und ungewichteten Kanten unterschieden werden” – Diese Aussage ist:

richtig

falsch

#5. “Der Knotengrad eines Graphen gibt die Menge der Knoten an, die sich im gesamten Graphen befinden. ” – diese Aussage ist:

richtig

falsch

Vorherige

Fertig

Ergebnisse