Um den kürzesten Weg in einem gewichteten Graphen zu ermitteln, kann der Bellman Ford Algorithmus eingesetzt werden. Auch bei Graphen, die über negative Kantengewichte verfügen, kann der Bellman Ford Algorithmus genutzt werden.
In diesem Kapitel zeigen wir dir, was man unter dem Bellman Ford Algorithmus versteht und warum er wichtig ist. Außerdem lernst du, wie der Bellman Ford angewendet wird und kannst dein Wissen anschließend mit Hilfe unserer Übungsaufgaben testen.
Synonym: Moore-Bellman-Ford-Algorithmus
Warum ist der Bellman Ford Algorithmus wichtig?
Viele Optimierungsprobleme im Operations Research von Unternehmen beschäftigen sich mit der Frage nach dem kürzesten Weg von einem Startpunkt zu allen anderen Knoten in einem Graphen. Da der Dijkstra Algorithmus nur genutzt werden kann, wenn keine negativen Kantengewichte im Graphen vorhanden sind, eignet sich in solchen Fällen der Bellman Ford Algorithmus wesentlich besser.
Was versteht man unter dem Bellman Ford Algorithmus?
Der Bellman Ford Algorithmus, benannt nach seinen Entwicklern Richard Bellman und Lester Ford, dient der Findung nach dem kürzesten Weg in einem Graphen. Während Kanten mit negativem Gewicht einbezogen werden können, muss darauf geachtet werden, dass Zyklen mit einem negativen Gewicht aus der Betrachtung ausgeschlossen werden.
Dazu wird zu jedem Knoten der jeweilige Vorgänger gesucht, welcher auf dem günstigsten Weg erreicht werden kann. Hierzu wird zunächst die Distanz zu jedem Knoten auf unendlich gesetzt.
Anschließend wird der Startknoten gewählt und dessen Distanz auf Null gesetzt. Im nächsten Schritt wird überprüft, ob die Kosten zum Ausgangsknoten, addiert mit den Kosten der jeweiligen Kante, gegenüber den bisher bekannten Kosten zum Zielknoten geringer sind. Ist eine Kante mit geringeren Kosten gefunden, so wurde ein günstigerer Weg entdeckt.
Anwendung des Bellman Ford Algorithmus
Die Anwendung des Bellman Ford Algorithmus wird anhand des folgenden Beispiels deutlich:
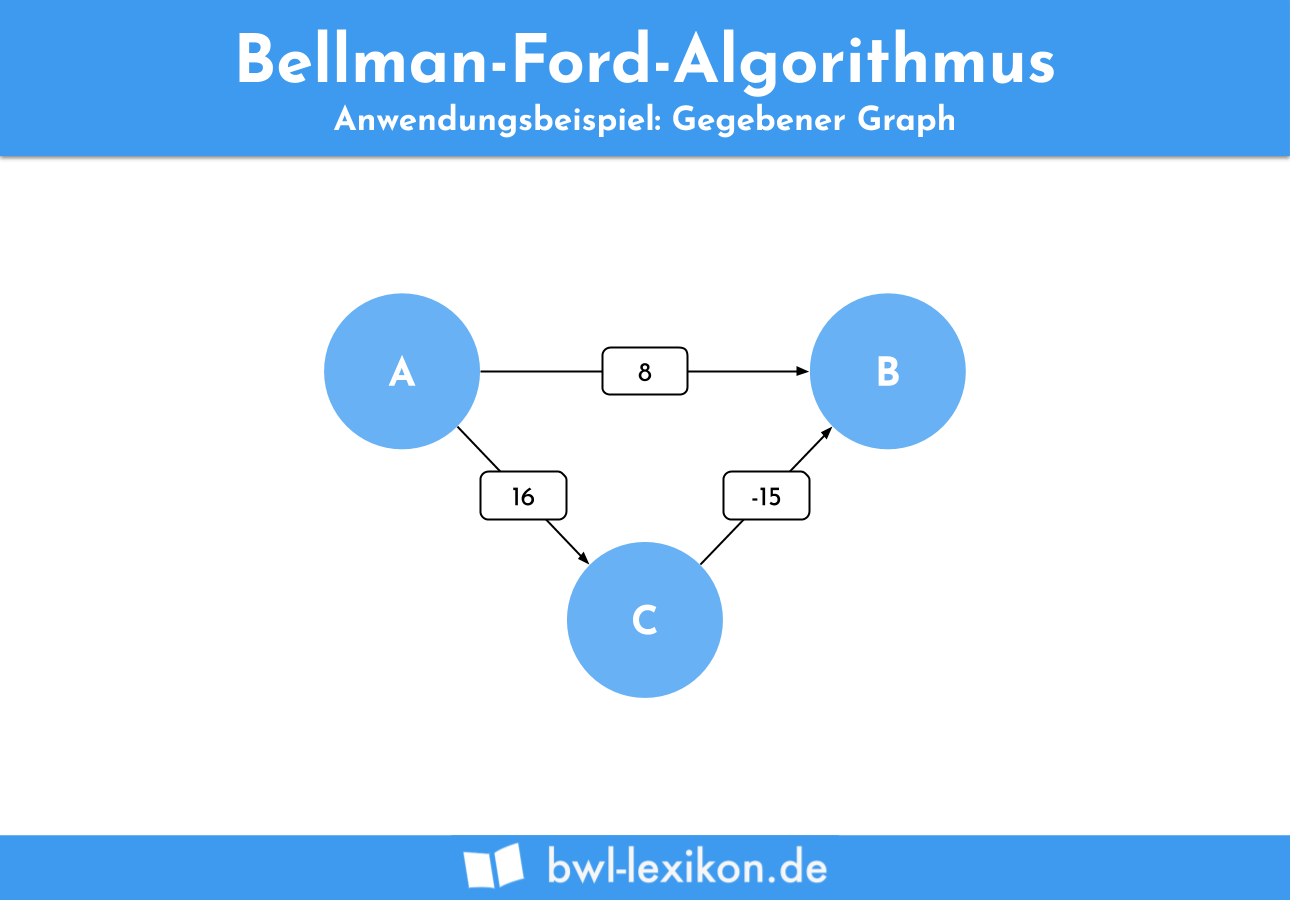
In diesem Graphen sollen die kürzesten Wege gefunden werden, die vom Startpunkt A ausgehen. Dazu nutzen wir den Bellman Ford Algorithmus.
Die Distanz zu A wird zu Beginn auf 0 gesetzt, zu allen Knoten auf unendlich.
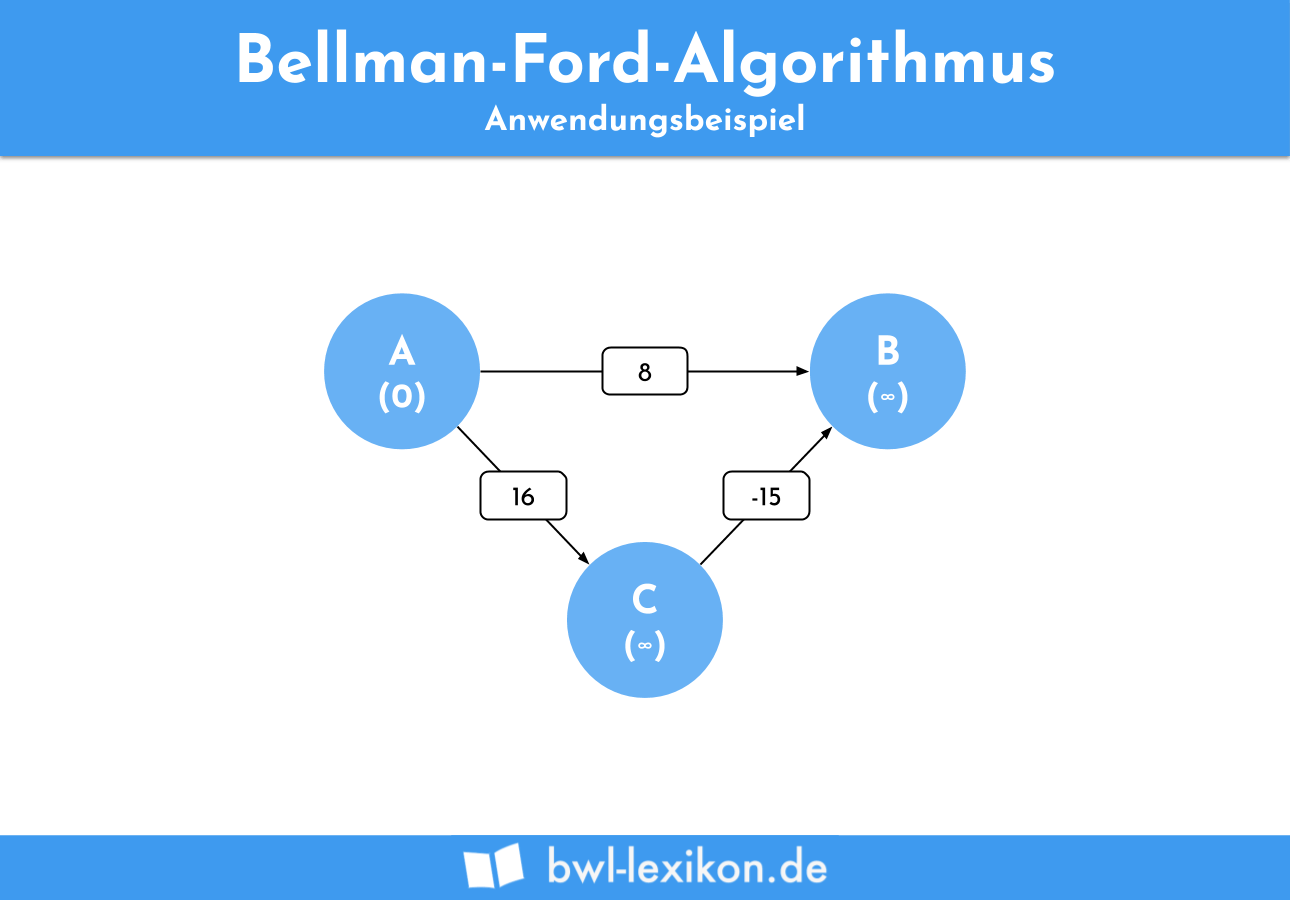
Anschließend werden die einzelnen Kanten überprüft, um einen möglichst kurzen Weg zu finden. Da im Graphen 3 Knoten existieren (n=3), muss jede Kante 2-mal (n-1) überprüft werden.
Zuerst überprüfen wir die Kante AB. Sie hat ein Kantengewicht von 8. Addiert mit den Kosten unseres Ausgangsknoten A (=0) liegen die Kosten also bei 8. Da dies günstiger als unendlich ist, können die aktuellen Kosten mit dem passenden Vorgänger notiert werden.
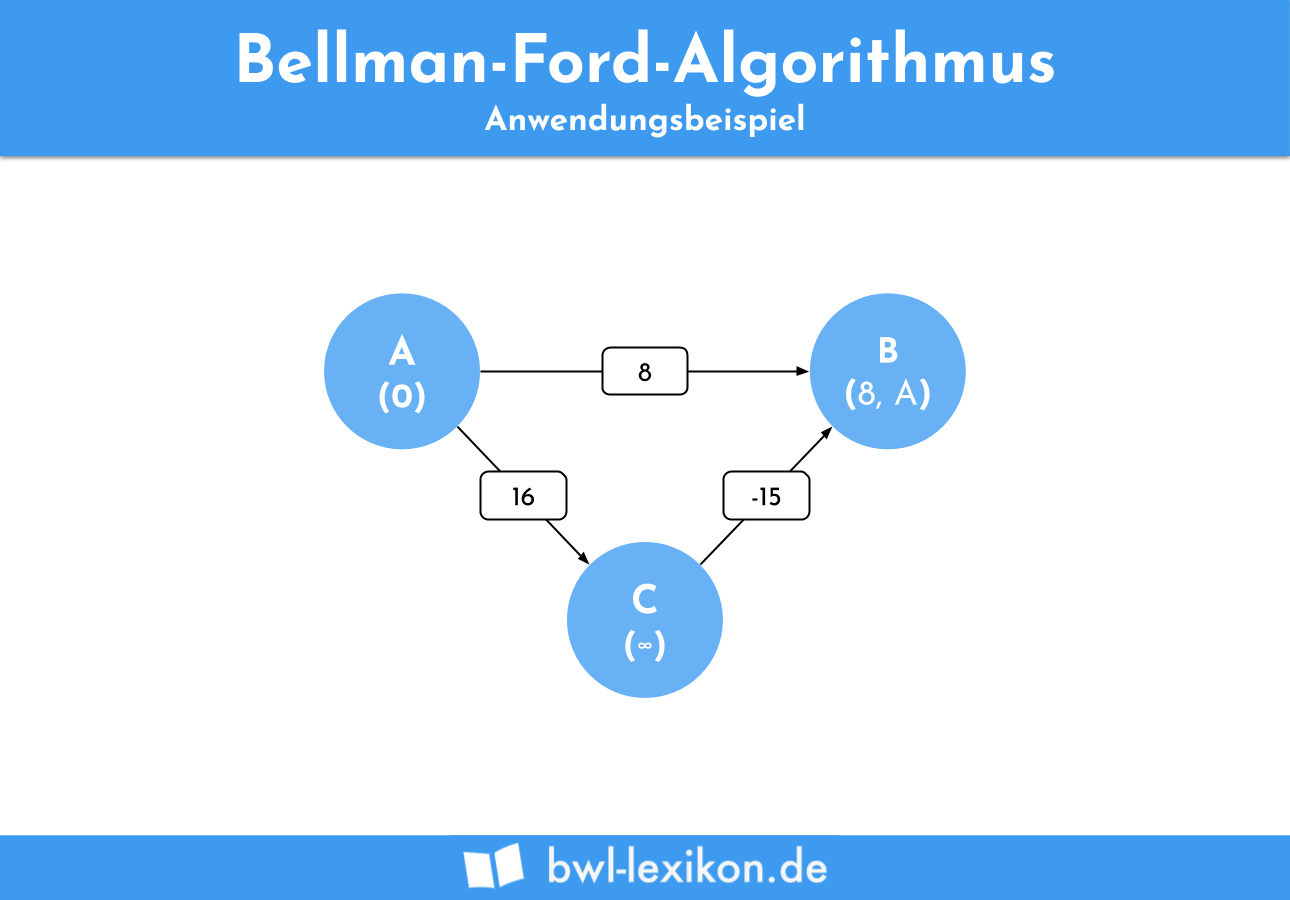
Als nächstes betrachten wir die Kante CB. Sie beginnt am Knoten C, dessen geringste Kosten aktuell bei unendlich liegen. Daher kann dieser Weg keine kürzere Distanz liefern. Als dritte Kante wird AC betrachtet. Die Summe aus den Kosten des Ausgangsknoten und dem Kantengewicht liegt bei 16. Auch dies tragen wir an unserem Graphen mit dem entsprechenden Vorgänger ein.
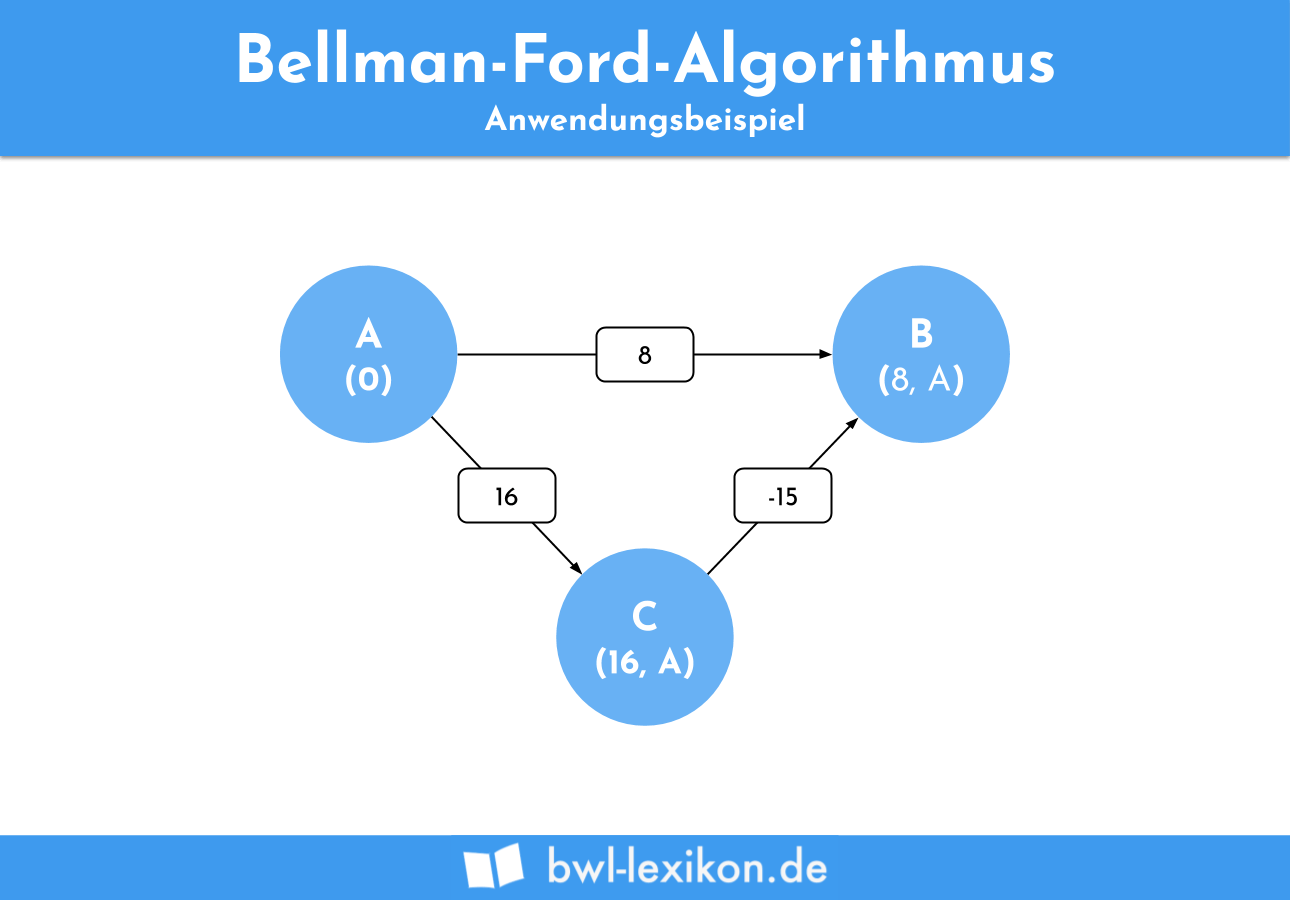
Der erste Durchlauf ist damit abgeschlossen. Aufgrund der 3 Knoten (n) im Graphen müssen wir alle Kanten jedoch zwei mal überprüfen (n-1). Überprüfen wir also die Kante AB erneut, stellen wir fest, dass die Distanz nicht geringer geworden ist. Wir können also unser vorheriges Ergebnis stehen lassen.
Bei der Überprüfung der Kante CB stellen wir fest, dass die Kosten des Vorgängers sich durch unsere vorherige Überprüfung verändert haben. Für die Kosten dieses Wegs rechnen wir nun also: 16 - 15 = 1.
Dadurch haben wir einen kürzeren Weg zum Knoten B mit einem neuen Vorgänger gefunden.
Dies tragen wir nun in unserem Graphen ein:
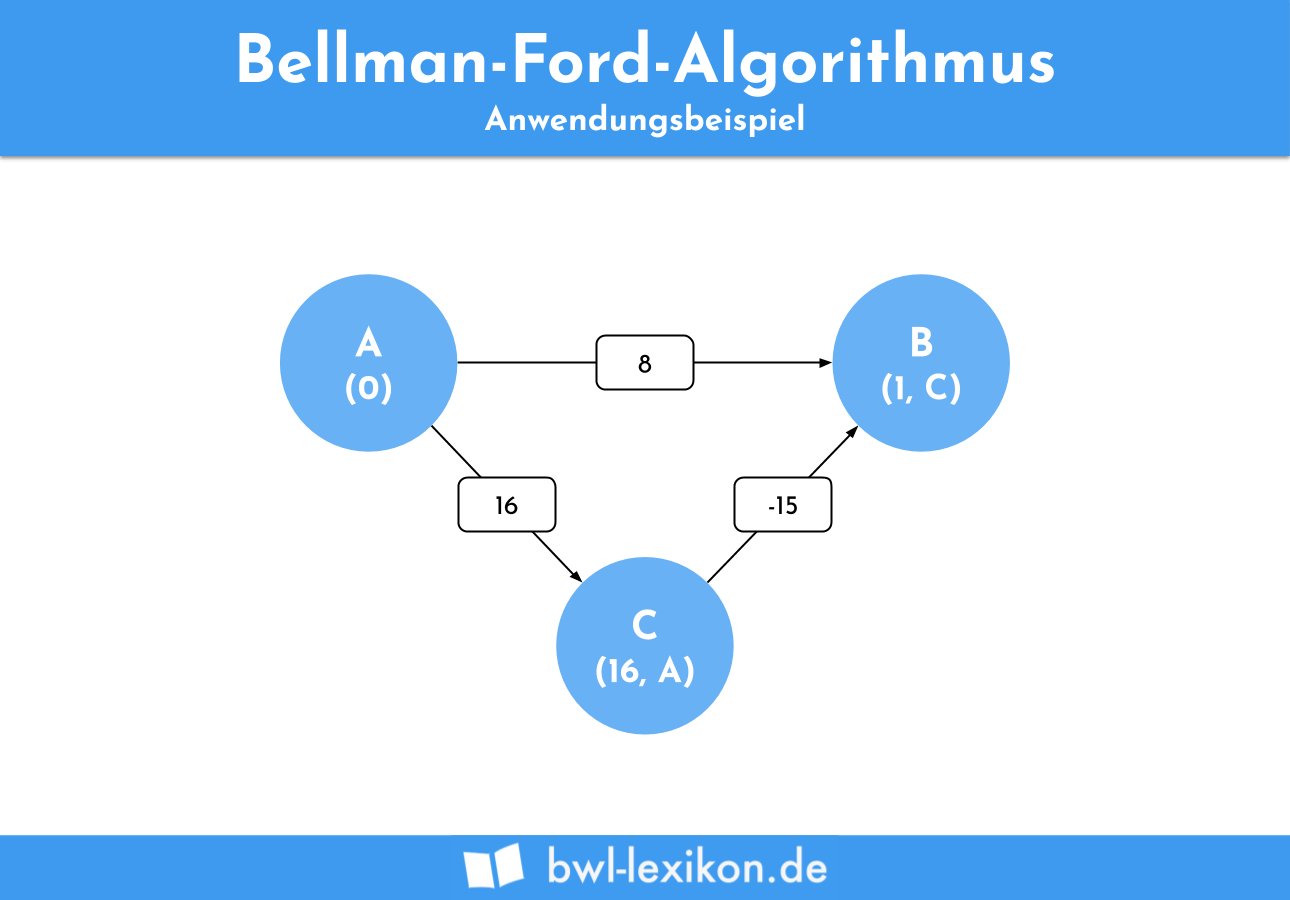
Bei der anschließenden Überprüfung der Kante AC stellen wir fest, dass kein neuer Weg gefunden werden kann, der günstiger als der bereits existierende Weg ist. Abschließend muss noch überprüft werden, ob im Graphen ein negativer Zyklus existiert.
Wir erkennen in unserem Graphen, dass das nicht der Fall ist, da auch bei erneuter Überprüfung der Kanten keine günstigeren Wege mehr gefunden werden können. Andernfalls würde der Algorithmus einen Fehler ausgeben, da kein eindeutig kürzester Weg existieren würde.
Um nun den kürzesten Weg von A nach B zu finden, schauen wir uns den Graphen rückwärts an. Gestartet bei Punkt B haben wir den günstigsten Vorgänger in C gefunden. Dieser hat den Vorgänger A.
Der kürzeste Weg von A nach C ist also:
A → B → C
Übungsfragen
#1. Was versteht man unter dem Bellman Ford Algorithmus?
#2. Wie wird der Bellman Ford Algorithmus angewendet?
#3. “Der Bellman Ford Algorithmus dient der Ermittlung des minimalen Spannbaums eines zusammenhängenden, gewichteten Graphen.” - diese Aussage ist:
#4. “Mit dem Bellman Ford Algorithmus können auch Graphen untersucht werden, die negative Kantengewichte enthalten.” - Diese Aussage ist:
#5. “Wie beim Dijkstra Algorithmus auch, darf zur Anwendung des Bellman Ford Algorithmus der Graph keine negativen Kantengewichte enthalten.” - diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen