Der Kruskal Algorithmus dient der Ermittlung des minimalen Spannbaums eines zusammenhängenden und gewichteten Graphen.
Wir zeigen dir in diesem Kapitel, warum der Kruskal Algorithmus wichtig ist, welche Probleme damit gelöst werden können und wie du ihn anwenden kannst. Nachdem du dir dieses Wissen angeeignet hast, kannst du dein Wissen anhand unserer Übungsaufgaben überprüfen.
Warum ist der Kruskal Algorithmus wichtig?
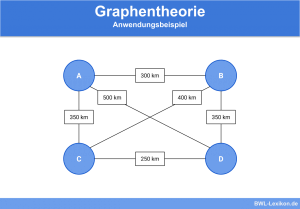
Im Operations Research eines Unternehmens geht es oft darum, auftretende Probleme optimal zu lösen. Hierbei kann der Kruskal Algorithmus helfen – insbesondere dann, wenn es um die Ermittlung des kostengünstigsten Wegs innerhalb eines Graphen geht, der alle Knoten des Graphen miteinander verbindet.
Dies ist beispielsweise dann wichtig, wenn eine optimale Verbindung zwischen verschiedenen Stationen gefunden werden muss, beispielsweise beim Ausbau eines Schienennetzes.
Was versteht man unter dem Kruskal Algorithmus?
Der Kruskal Algorithmus gehört zur Gruppe der Greedy Algorithmen. Er kann bei zusammenhängenden, gewichteten Graphen angewendet werden, um den minimalen Spannbaum zu ermitteln. Der minimale Spannbaum beschreibt den Teilgraph, der die Kanten beinhaltet, die die kostengünstigste Verbindung aller Knoten innerhalb des Graphen beschreibt.
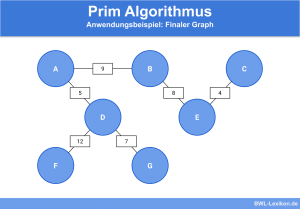
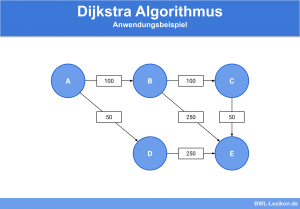
Ein weiterer Algorithmus, der ebenfalls zur Findung des minimalen Spannbaums eines Graphen dient, ist der Prim Algorithmus. Allerdings funktionieren beide Algorithmen unterschiedlich. Während beim Prim Algorithmus mit einem Knoten gestartet wird und immer die günstigste Kante hinzugefügt wird, beginnt der Kruskal Algorithmus mit allen Knoten ohne Kanten. Nacheinander werden dann die global günstigsten Kanten hinzugefügt.
Beispiel: Anwendung des Kruskal Algorithmus
Um die Funktionsweise des Kruskal Algorithmus zu verstehen, schauen wir uns ein Beispiel an.
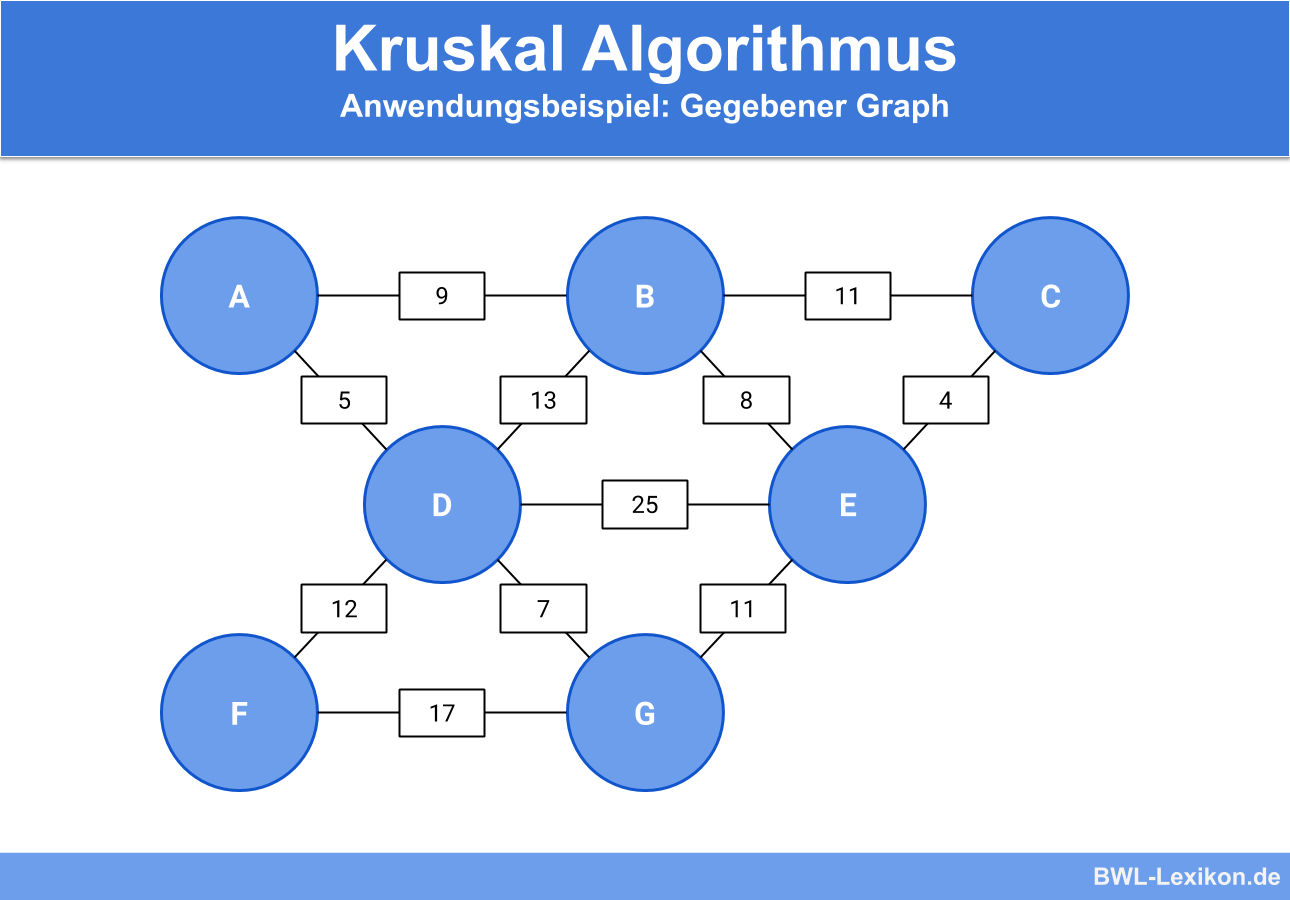
Um den minimalen Spannbaum des Graphen zu finden, nutzten wir den Kruskal Algorithmus.
Hierbei werden zuerst alle im Graph enthaltenen Kanten aufsteigend nach ihrem Gewicht sortiert:
| Kante | Kosten |
|---|---|
| CE | 4 |
| AD | 5 |
| DG | 7 |
| BE | 8 |
| AB | 9 |
| EG | 11 |
| BC | 11 |
| DF | 12 |
| BD | 13 |
| FG | 17 |
| DE | 25 |
Anschließend wird ein neuer Graph erstellt, der zunächst nur die Knoten des ursprünglichen Graphen ohne die jeweiligen Kanten enthält.
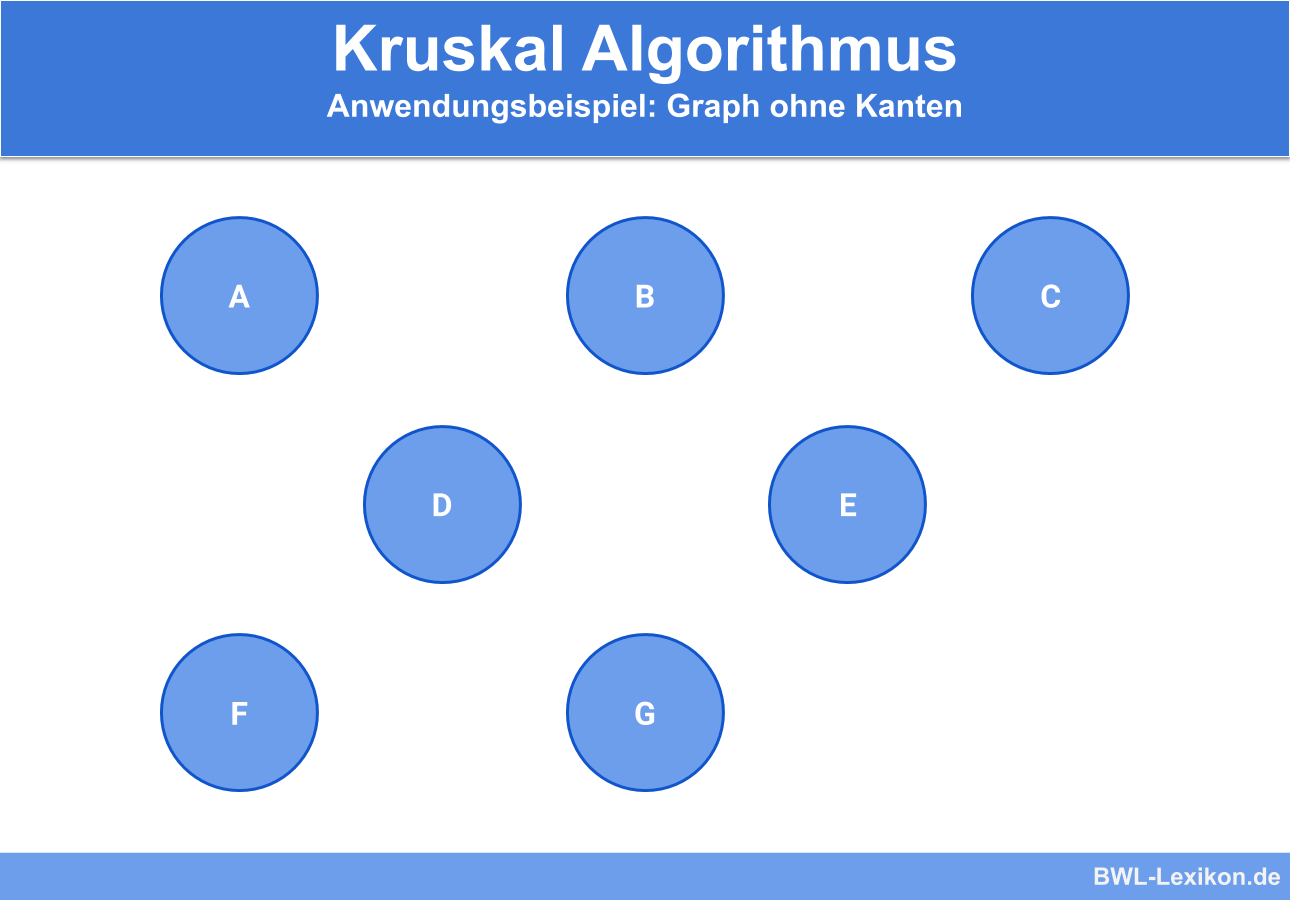
Anschließend werden die Kanten in der vorher sortierten Reihenfolge eingefügt, beginnend mit der Kante, die das geringste Kantengewicht besitzt. In unserem Beispiel ist das die Kante CE mit einem Kantengewicht von 4.
Diese fügen wir also als erstes in unseren neuen Graphen ein:

Nach der Kante CE betrachten wir nun die nächst kürzere Kante. Das ist Kante AD mit einem Kantengewicht von 5.
Auch diese Kante fügen wir in unseren neuen Graphen ein:
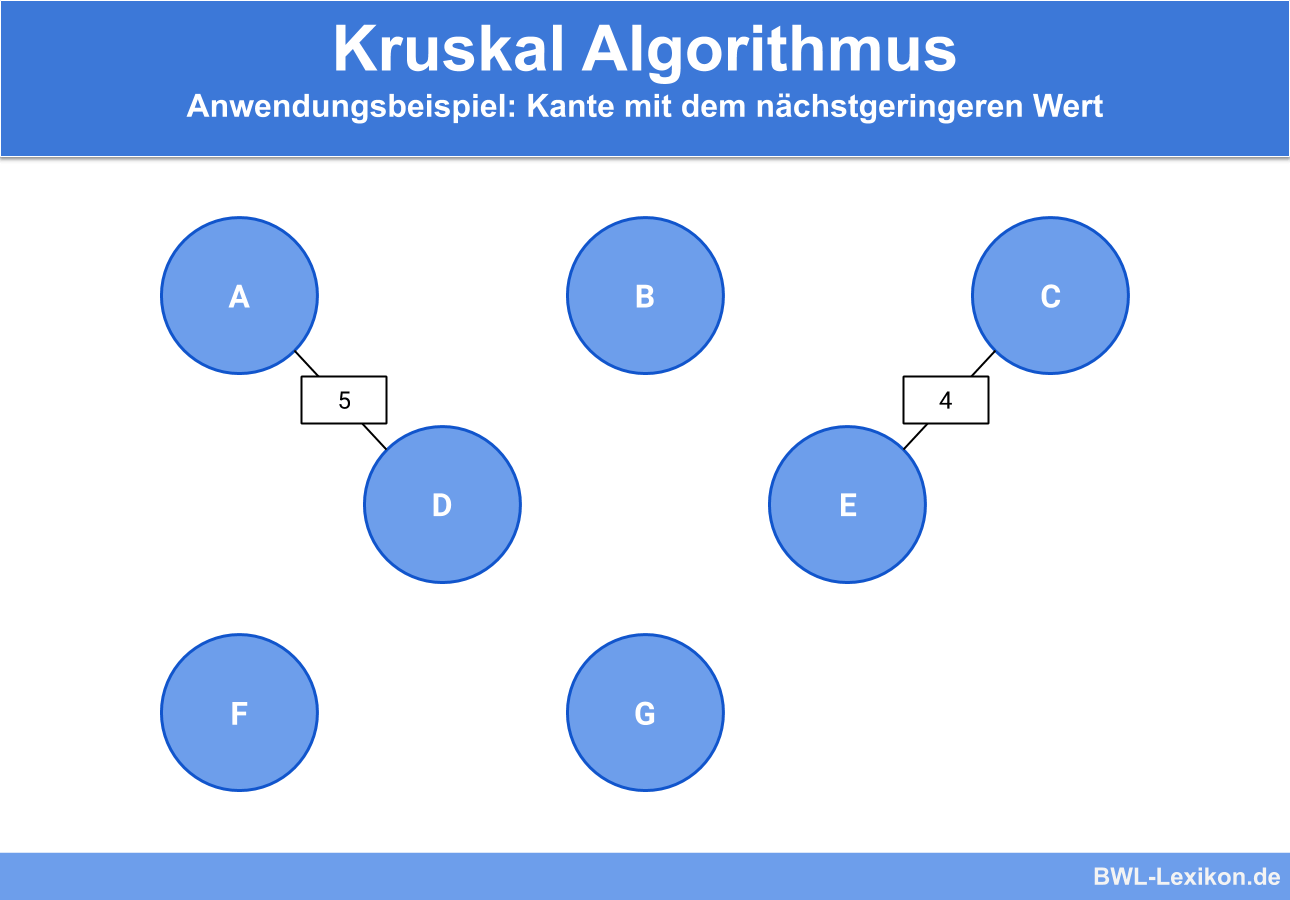
Diesen Vorgang wiederholen wir nun für die nächsten Kanten aus unserer vorherigen Sortierung. Sind wir bei Kante EG angekommen, stellen wir fest, dass EG und BC das gleiche Kantengewicht besitzen.
Grundsätzlich kann sich nun eine der Kanten ausgesucht werden. Zu beachten ist dabei, dass im Zuge des Kruskal Algorithmus nur Kanten berücksichtigt werden, die keine Kreise bilden.
Fügen wir die Kante EG ein, so sehen wir, dass ein Kreis im Graphen entstehen würde. Das gleiche passiert, wenn wir die Kante BC einfügen würden. Demnach werden beide Kanten übersprungen und nicht in unseren neuen Graphen eingefügt.
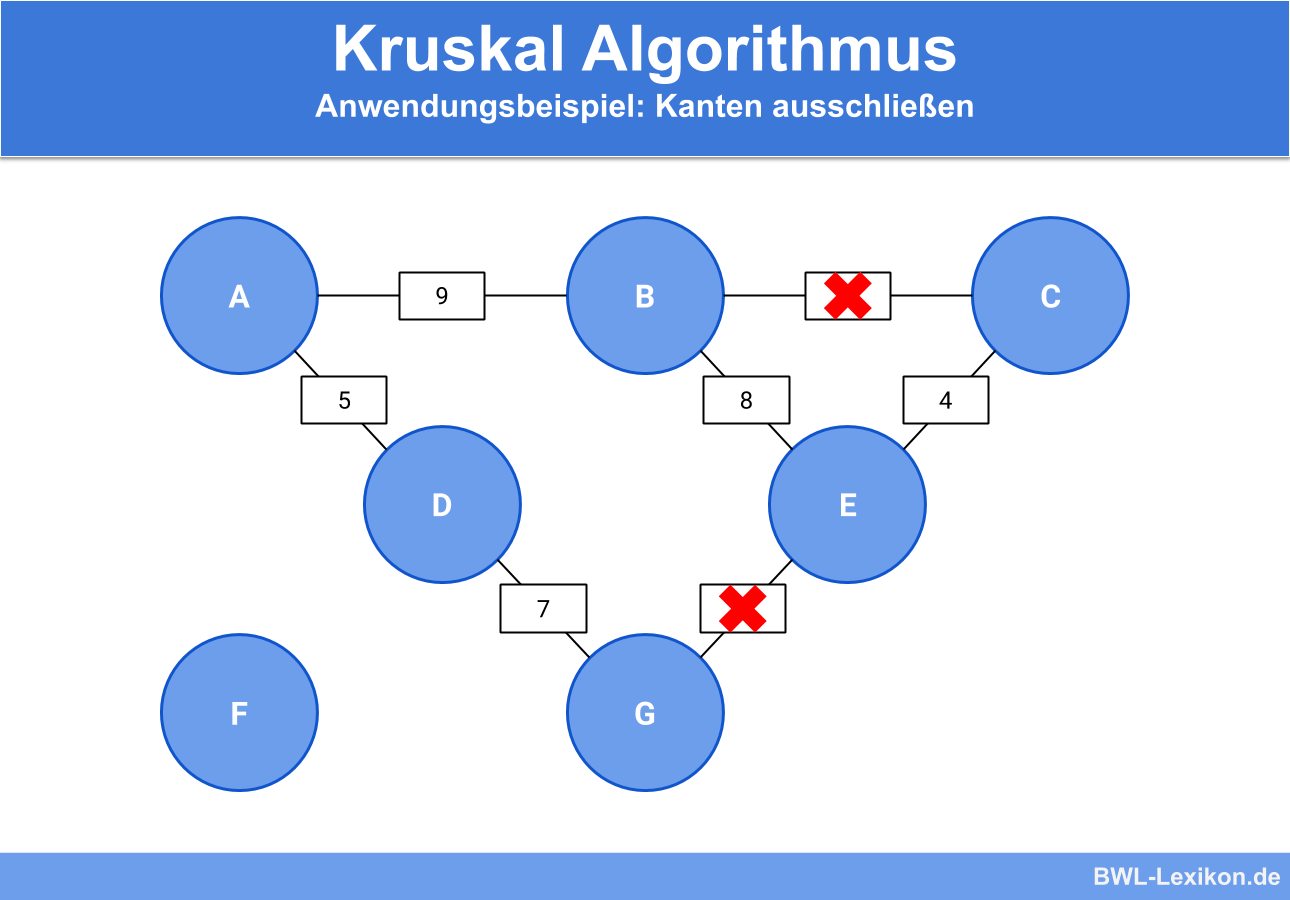
Als nächste Kante betrachten wir DF mit dem Kantengewicht 12. Das Einfügen dieser Kante führt nicht zu einer Kreisbildung, weshalb wir sie in unseren Graphen einfügen können.
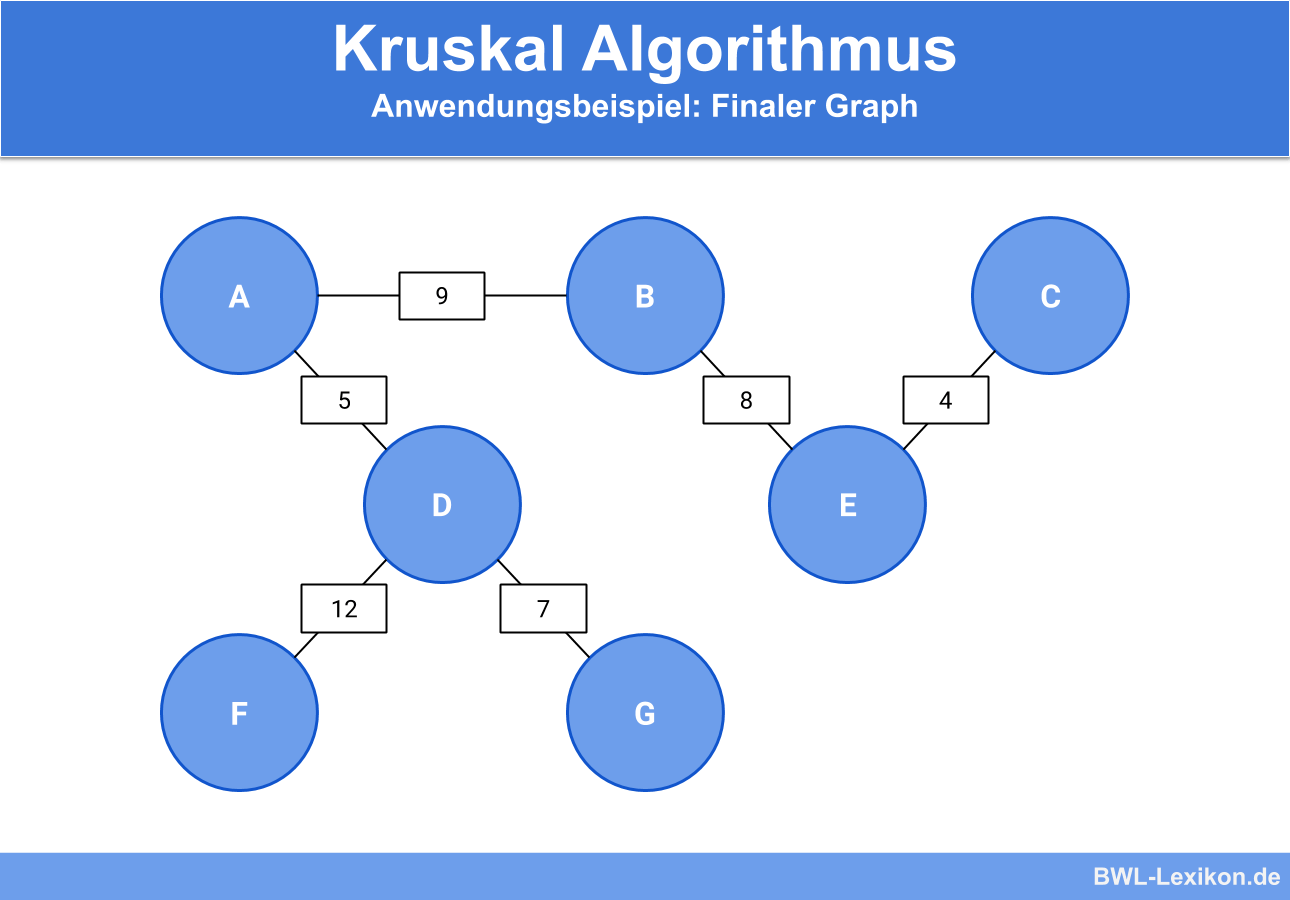
Mit dem Einfügen der Kante DF können wir erkennen, dass nun alle Knoten miteinander verbunden sind. Wir haben also den minimalen Spannbaum des Graphen gefunden. Alle weiteren Kanten würden zu Kreisen im Graphen führen, weshalb wir sie vernachlässigen können.
Unser neuer Graph ist nun fertig:
Übungsfragen
#1. Was versteht man unter dem Kruskal Algorithmus?
#2. Wie wird der Kruskal Algorithmus angewendet?
#3. “Der Kruskal Algorithmus dient der Findung des minimalen Spannbaums eines zusammenhängenden, gewichteten Graphen” - diese Aussage ist:
#4. “Beim Kruskal Algorithmus werden Kanten, die Kreise innerhalb des Graphen bilden nicht berücksichtigt.” - Diese Aussage ist:
#5. “Der Kruskal Algorithmus kann nur in ungewichteten Graphen angewendet werden.” - diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen