Gerichtete / ungerichtete Graphen

Gerichtete und ungerichtete Graphen sind Elemente der Graphentheorie, einer mathematischen Methode zur Lösung einer Vielzahl von algorithmischen Problemen. Der Unterschied zwischen beiden besteht darin, dass gerichtete Graphen nur in einer Richtung genutzt werden können, bei ungerichteten jedoch keine Richtung vorgegeben ist.

Wir zeigen dir in diesem Abschnitt, warum gerichtete und ungerichtete Graphen wichtig sind und welche Bedeutung sie in der betrieblichen Anwendung haben. Abschließend kannst du dein Wissen anhand einiger Übungsaufgaben überprüfen.

Warum sind gerichtete und ungerichtete Graphen wichtig?

Die Graphentheorie als ein Teilgebiet der Mathematik kann auch zur Untersuchung und Lösung betriebswirtschaftlicher Fragestellungen und Probleme herangezogen werden. Dabei kann die Richtung der Graphen eine entscheidende Rolle zur Herangehensweise und Lösung des Problems spielen. Aus diesem Grund ist bei der Untersuchung des aufgestellten Graphenmodells wichtig darauf zu achten, ob es sich um einen gerichteten oder ungerichteten Graphen handelt.

Was versteht man unter gerichteten und ungerichteten Graphen?

In der Graphentheorie besteht ein ein Graph G immer aus den folgenden Elementen:

• der Menge von Knoten V
• der Menge von Kanten E

Zur Entstehung eines Graphen sind die jeweiligen Knotenpunkte immer durch entsprechende Kanten miteinander verbunden. Je nach Art der Kanten kann man zwischen gerichteten und ungerichteten Graphen unterscheiden.

Was macht gerichtete Graphen aus?

In gerichteten Graphen haben die Kanten zwischen den Knoten die Eigenschaft, dass sie nur in bestimmte Richtungen genutzt werden können. Hierbei werden die Kanten als Pfeile dargestellt, um die Richtung in der sie genutzt werden können abzubilden:

Beispiel

Der Auslieferungsfahrer der “DeliverX AG” muss auf seiner Tagesroute vier Pakete an unterschiedlichen Adressen in der Altstadt ausliefern. Da die Altstadt von engen Gassen geprägt ist, ist ein Großteil davon als Einbahnstraße ausgeschildert.

Die Wege können also nur in eine Richtung befahren werden. Um die optimale Route zu planen, stellt er das Straßennetz als gerichteten Graph dar. Start- und Endpunkt ist jeweils das Depot des Unternehmens. Außerdem soll jede Adresse nur einmal angefahren werden.

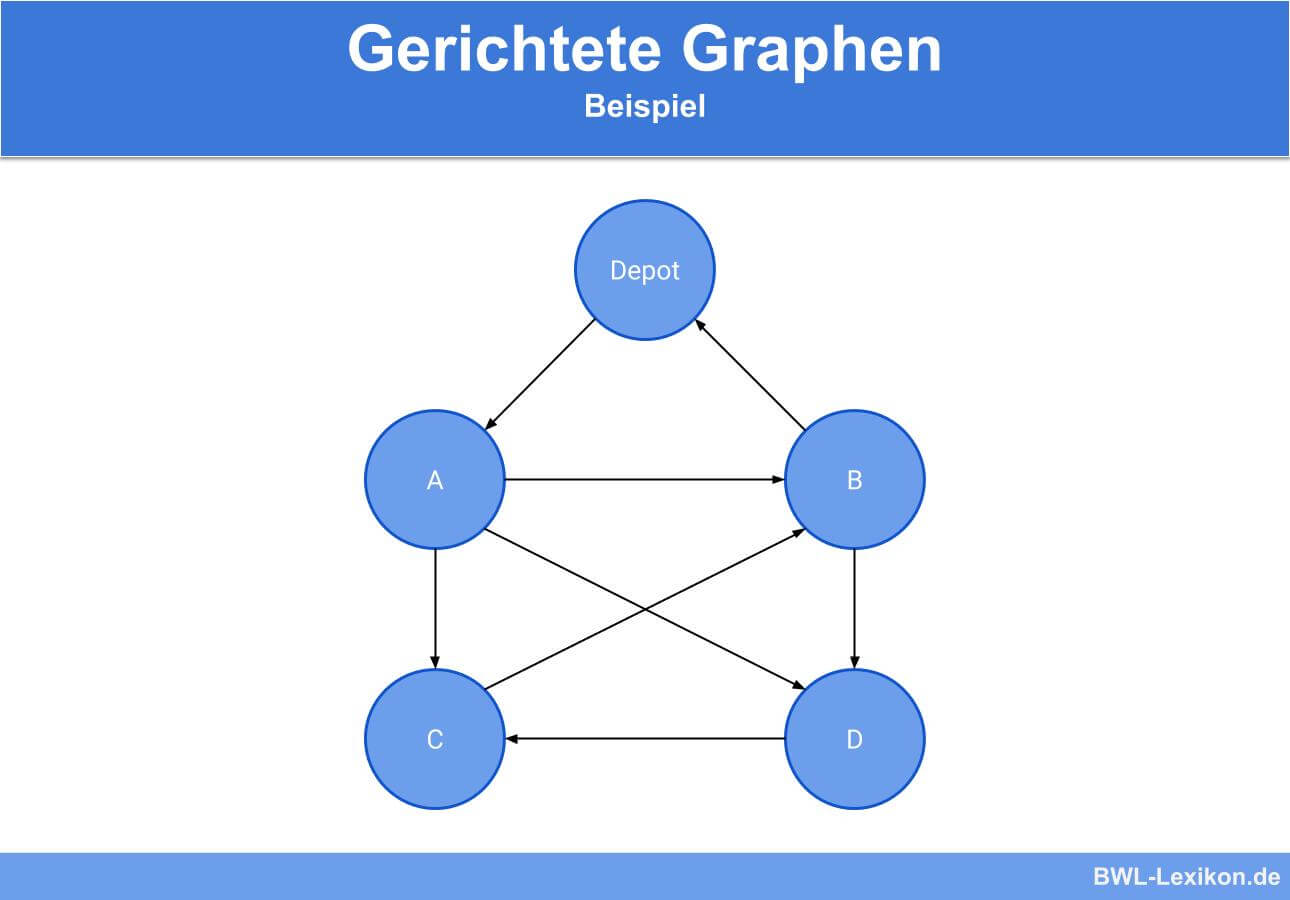
Anhand des gerichteten Graphen ist zu erkennen, dass die erste logische Route Depot → A → B → C → D → Depot nicht möglich ist, da die Kante zwischen den Knoten C und D in dieser Richtung nicht genutzt werden kann. Die einzig mögliche Route, die alle Bedingungen für die Auslieferung der Pakete erfüllt, ist demnach Depot → A → D → C → B → Depot.

Was macht ungerichtete Graphen aus?

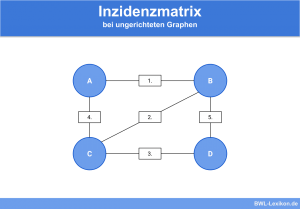
Im Gegensatz zu gerichteten Graphen spielt bei ungerichteten Graphen die Richtung der Kanten keine Rolle.

Sie können in beide Richtungen genutzt werden und werden daher als einfache Verbindungslinie dargestellt:

Beispiel

Der Auslieferungsfahrer der “DeliverX AG” muss am nächsten Tag wieder vier Pakete an unterschiedliche Adressen ausliefern. Diesmal ist er allerdings im Neubaugebiet der Stadt unterwegs. Hier sind die Straßen breit genug angelegt, sodass es für jede Fahrtrichtung mindestens eine Fahrspur gibt.

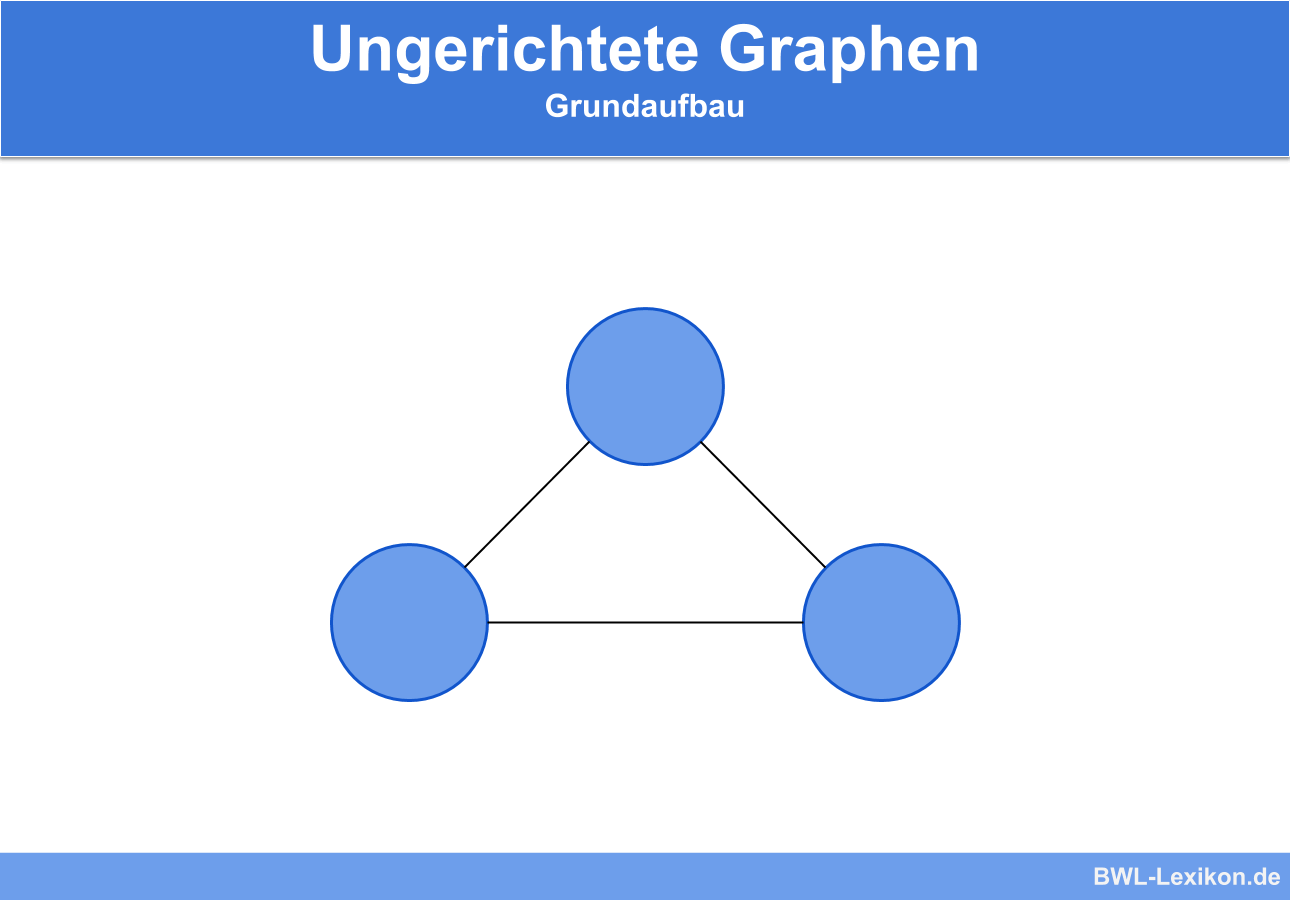
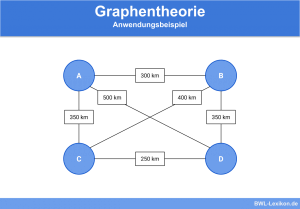
Das Straßennetz kann also ungerichteter Graph dargestellt werden:

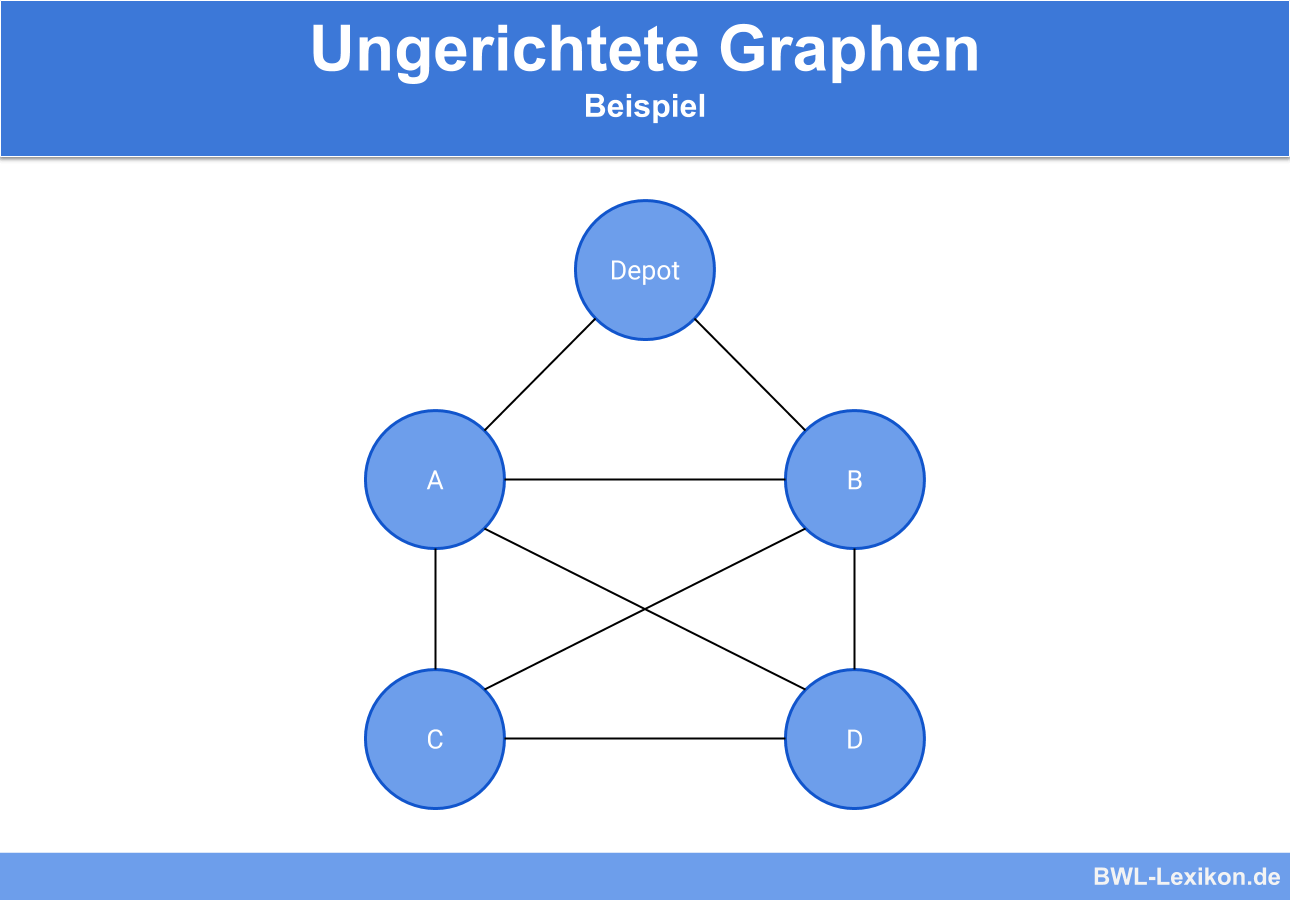
Es gibt diesmal also verschiedene Möglichkeiten, die Pakete auszuliefern. Um die bestmögliche Route wählen zu können, müsste der Auslieferungsfahrer noch eine weitere Eigenschaft von Graphen in Betracht ziehen: die Gewichtung. Hierbei unterscheidet man zwischen gewichteten und ungewichteten Graphen.

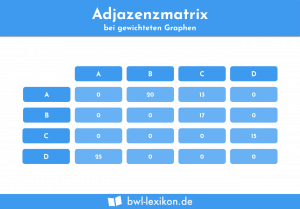
Bei gewichteten Graphen sind die Kanten unterschiedlich lang, ungewichtete haben gleiche Kantenlängen oder die Länge der Kanten ist für die Betrachtung irrelevant. In unserem Beispiel würde die Kantenlänge also die Wege-Kilometer zwischen den einzelnen Adressen darstellen. Mit Hilfe dieser Angabe könnte der Auslieferungsfahrer die kürzeste Route ermitteln, welche als optimal anzusehen ist.

Übungsfragen

 

#1. Was versteht man unter gerichteten Graphen?

Graphen, bei denen die Längen der Kanten unterschiedlich sind, werden als gerichtete Graphen bezeichnet.

Graphen, bei denen die Kanten in beide Richtungen nutzbar sind, werden als gerichtete Graphen bezeichnet.

Graphen, bei denen die Kanten nur in eine bestimmte Richtung nutzbar sind, werden als gerichtete Graphen bezeichnet.

#2. Was versteht man unter ungerichteten Graphen?

Graphen, bei denen die Längen der Kanten unterschiedlich sind, werden als ungerichtete Graphen bezeichnet.

Graphen, bei denen die Kanten in beide Richtungen nutzbar sind, werden als ungerichtete Graphen bezeichnet.

Graphen, bei denen die Kanten nur in eine bestimmte Richtung nutzbar sind, werden als ungerichtete Graphen bezeichnet.

#3. Welche Elemente sind grundsätzlich Bestandteil eines Graphen?

Die Menge der Knoten V und die Menge der Kanten E

Die Menge der Richtungen R und die Menge der Knoten V

Die Menge der Knoten V und die Menge der Graphen G

#4. “Neben der Richtung von Kanten können Graphen auch in Bezug auf ihre Gewichtung unterschieden werden” – Diese Aussage ist:

richtig

falsch

#5. “Der Unterschied zwischen gerichteten und ungerichteten Graphen ist für die Lösung betriebswirtschaftlicher Probleme irrelevant.” – diese Aussage ist:

richtig

falsch

Vorherige

Fertig

Ergebnisse