In der Inzidenzmatrix werden die Beziehungen der Knoten und der Kanten eines Graphen abgebildet.
In diesem Kapitel zeigen wir dir, was eine Inzidenzmatrix ist, warum Sie wichtig ist und wie du anhand eines Graphen die entsprechende Inzidenzmatrix erstellen kannst. Im Anschluss kannst du dieses erworbene Wissen mit Hilfe unserer Übungsaufgaben testen.
Synonym: Knoten-Kanten-Matrix
Warum ist die Inzidenzmatrix wichtig?
Die Informationen aus einem Graphen dienen im betrieblichen Umfeld oft als Grundlage für wichtige Entscheidungen. Um diese Informationen effektiv nutzen zu können, müssen sie jedoch meist erst weiterverarbeitet oder zumindest gespeichert werden. Einen Graphen in entsprechenden Computerprogrammen weiterzuverarbeiten ist nur unter Zuhilfenahme einer Matrix-Darstellung der Informationen möglich.
In der Inzidenzmatrix lassen sich also die Beziehungen der Knoten und Kanten eines Graphen in einer Form darstellen, die sich für die Speicherung und Weiterverarbeitung bestens eignet.
Was versteht man unter einer Inzidenzmatrix?
“Inzidenz” beschreibt in der Geometrie die Eigenschaft gemeinsame Punkte zu besitzen. In einem Graphen beschreibt die Inzidenz also, ob die Knoten einen gemeinsamen Punkt mit den entsprechenden Kanten haben, bzw. ob von einem Knoten eine entsprechende Kante ausgeht.
Bei der Inzidenzmatrix handelt es sich um eine “n x m Matrix”, wobei n die Anzahl der Knoten und m die Anzahl der Kanten im Graphen darstellt. Durch die Eintragungen in der Matrix lässt sich erkennen, ob der Knoten an der entsprechenden Kante liegt oder nicht. Um dieses darzustellen, werden die Knoten und Kanten entsprechend durchnummeriert.
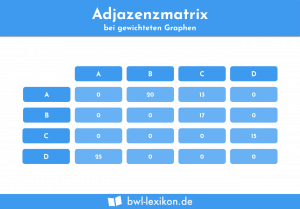
Das Gegenstück zur Inzidenzmatrix ist die Adjazenzmatrix.
Inzidenzmatrix bei ungerichteten Graphen
In einem ungerichteten Graphen können die Kanten zwischen zwei Knoten in beide Richtungen genutzt werden.
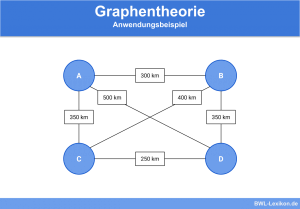
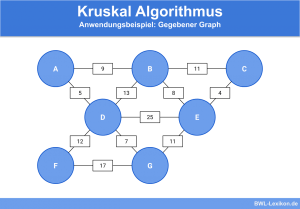
Um die Erstellung einer Inzidenzmatrix eines ungerichteten Graphen zu verdeutlichen, schauen wir uns folgendes Beispiel an:
Die Zahlen an den Kanten stellen hierbei keine Kantengewichte dar, wie es bei einem gewichteten Graphen der Fall ist. Sie dienen lediglich der Nummerierung der Kanten, die wir für die Erstellung der Inzidenzmatrix benötigen. Anhand des Graphen erkennen wir, dass 4 Knoten und 5 Kanten existieren. dementsprechend erstellen wir eine “4×5-Matrix”.
Neben der Anzahl an Knoten und Kanten können wir folgendes in dem Graphen erkennen:
- Der Knoten A liegt an den Kanten 1. und 4. an.
- Der Knoten B liegt an den Kanten 1., 2. und 5. an.
- Der Knoten C liegt an den Kanten 2., 3. und 4. an.
- Der Knoten D liegt an den Kanten 3. und 5. an.
Diese Informationen übertragen wir nun in unsere eben erstellte Matrix. Dabei tragen wir eine “1” ein, wenn der Knoten an der entsprechenden Kante anliegt und eine “0” wenn der Knoten nicht an der entsprechenden Kante anliegt. Die daraus entstehende Inzidenzmatrix sieht also folgendermaßen aus:
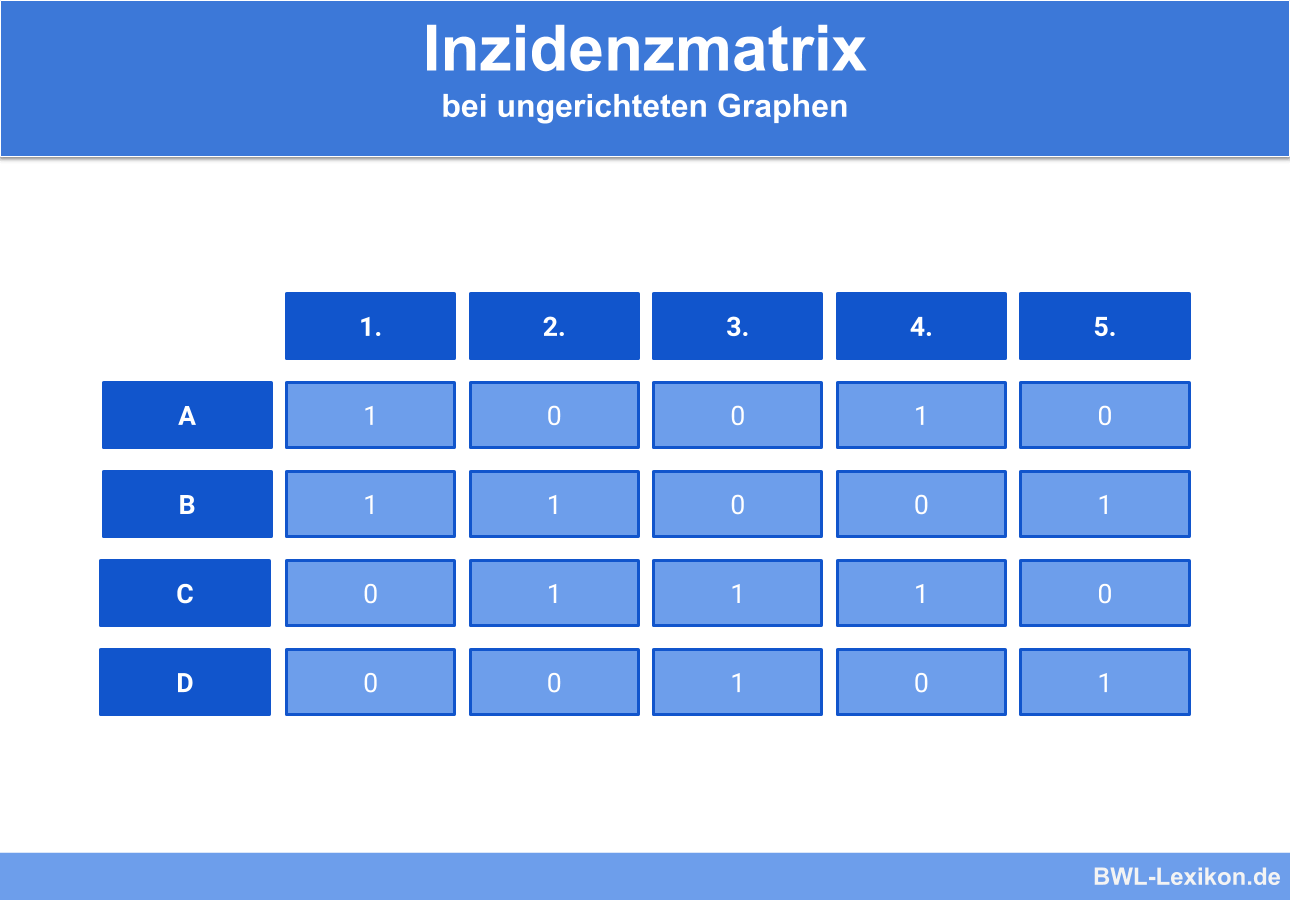
Zwei Knoten sind immer genau durch eine Kante verbunden. Die Richtung der Kanten ist bei einem ungerichteten Graphen egal. Demnach ergibt die Summe einer Spalte immer 2.
Inzidenzmatrix bei gerichteten Graphen
Bei einem gerichteten Graphen spielen die Richtungen der Kanten eine wesentliche Rolle. Dementsprechend müssen diese auch in der Inzidenzmatrix dargestellt werden. Hierbei wird unterschieden, ob ein Knoten der Start- oder der Endpunkt einer Kante ist.
- Bildet ein Knoten den Startpunkt einer Kante, so wird dies mit dem Eintrag “1” dargestellt.
- Bildet ein Knoten den Endpunkt einer Kante, so wird stattdessen ein “-1” eingetragen.
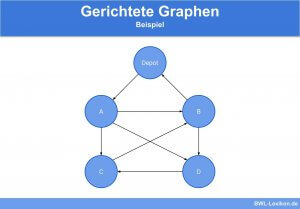
Schauen wir uns zur Verdeutlichung folgendes Beispiel an:
Anhand dieses Graphen können wir folgende Informationen ablesen:
- Der Knoten A bildet den Startpunkt der Kante 1. und den Endpunkt der Kante 4.
- Der Knoten B bildet den Startpunkt der Kante 2. und den Endpunkt der Kanten 1. und 5.
- Der Knoten C bildet den Startpunkt der Kanten 3. und 4. und den Endpunkt der Kante 2.
- Der Knoten D bildet den Startpunkt der Kante 5. und den Endpunkt der Kante 3.
Diese Informationen stellen wir nun in einer Inzidenzmatrix dar. Diese sieht dann folgendermaßen aus:
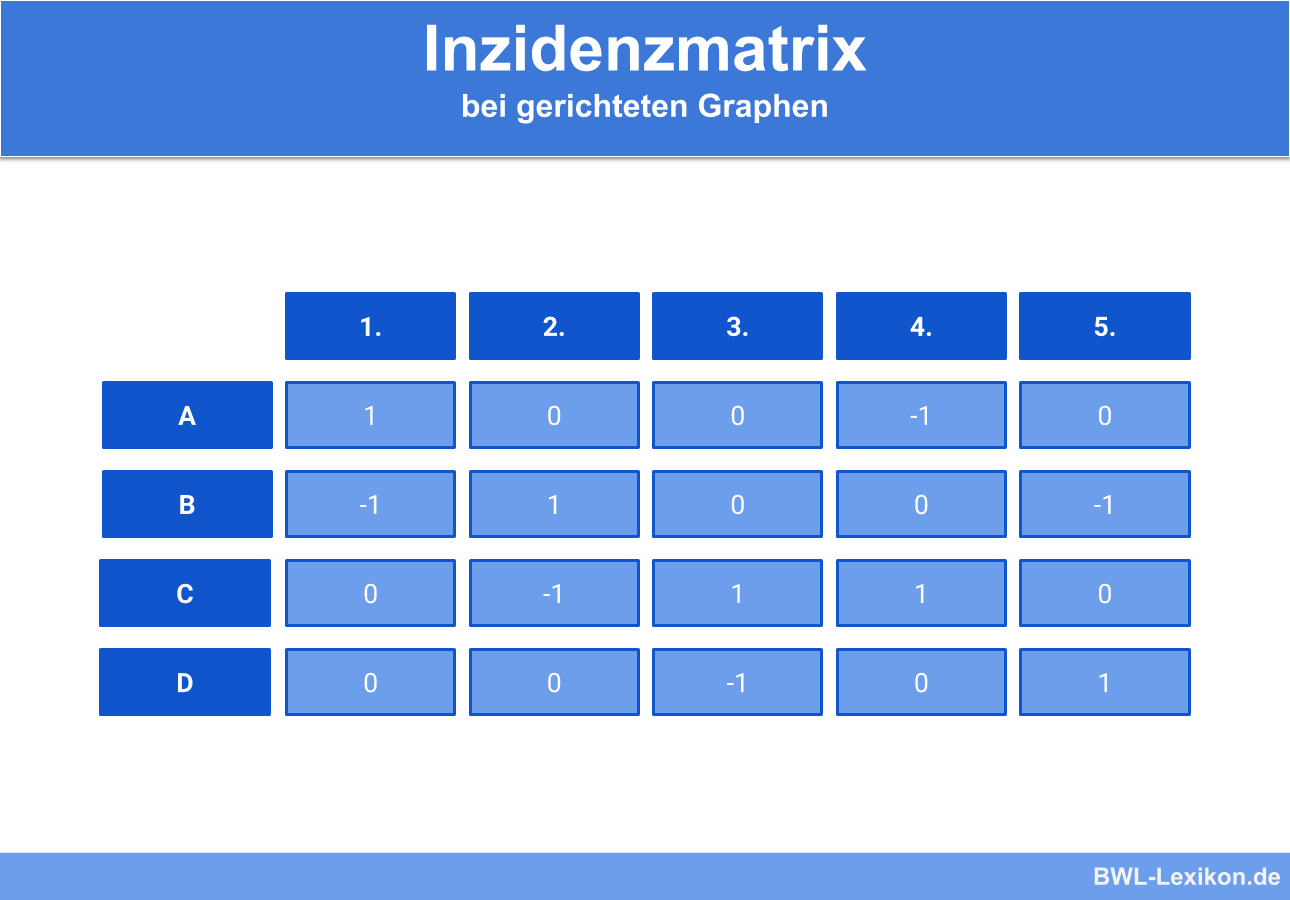
Da jede Kante genau einen Start- und einen Endpunkt besitzt, findet sich in jeder Spalte ein Eintrag “1” und ein Eintrag “-1”. Dementsprechend ergibt die Summe einer Spalte in der Inzidenzmatrix von gerichteten Graphen 0.
Weitere Form der Inzidenz-Darstellung: Die Inzidenzliste
Die Beziehung der Knoten und Kanten eines Graphen kann auch in einer Inzidenzliste dargestellt werden. Dabei gilt:
- Für jeden Knoten werden die Knoten aufgeführt, zu denen eine Kante führt.
Für den folgenden ungerichteten Graphen soll die entsprechende Inzidenzliste erstellt werden:
In der Inzidenzliste tragen wir nun also für jeden Knoten die Knoten ein, zu denen eine Verbindung besteht:
Bei einem gerichteten Graphen dagegen werden nur die Knoten aufgeführt, zu denen eine Kante von dem betrachteten Knoten aus hinführt.
Dazu schauen wir uns den folgenden gerichteten Graphen an:
Hierbei müssen die Richtungen der Kanten betrachtet werden, um zu erkennen, zu welchen Knoten eine Kante vom betrachteten Knoten aus führt.
Die Inzidenzliste sieht dementsprechend folgendermaßen aus:
Übungsfragen
#1. Was versteht man unter einer Inzidenzmatrix?
#2. Wozu dient eine Inzidenzmatrix?
#3. “Die Inzidenzmatrix enthält den gleichen Informationsgehalt wie der Graph selbst.” – diese Aussage ist:
#4. “Die Summe einer Spalte in einer Inzidenzmatrix eines ungerichteten Graphen ist immer 0.” – Diese Aussage ist:
#5. “Die Summe einer Spalte in einer Inzidenzmatrix eines gerichteten Graphen ist immer 2” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
