Die Adjazenzmatrix ist eine Matrix, die die Anzahl der Knoten in einem Graphen und deren Beziehungen zueinander darstellt. Damit lässt sich darstellen, wie viele Knoten in einem Graphen existieren, welche Kanten zwischen Ihnen bestehen und zu welchen Kosten.
Dieses Kapitel erläutert dir, was eine Adjazenzmatrix ist, welchen Nutzen Sie hat und welche Informationen du aus ihr gewinnen kannst. Das gesammelte Wissen kannst du anschließend anhand unserer bereitgestellten Übungsaufgaben überprüfen.
Synonym: Nachbarschaftsmatrix
Warum ist die Adjazenzmatrix wichtig?
Mithilfe einer Adjazenzmatrix lassen sich die Knoten und Kanten eines Graphen sowie deren Kosten bzw. Gewichte in vereinfachter Form darstellen. Dies ist besonders wichtig, wenn die Eigenschaften eines Graphen im Computer gespeichert werden sollen, um eine weitere Verarbeitung mittels Methoden der linearen Algebra oder Algorithmen zu gewährleisten.
So können mithilfe spezieller Softwareprogramme beispielsweise Routenplanungen vorgenommen, Netzpläne erstellt oder andere Analysen des Graphen durchgeführt werden. Ein Beispiel für die Anwendung einer Adjazenzmatrix ist der PageRank-Algorithmus vieler Online-Suchmaschinen.
Was versteht man unter einer Adjazenzmatrix?
“Adjazenz” – abgeleitet vom lateinischen “adjazent” = “Anwohner” – bedeutet so viel wie Nachbarschaft. Demnach stellt die Adjazenzmatrix die nachbarschaftlichen Beziehungen der Knoten eines Graphen zueinander dar.
Die Adjazenzmatrix ist eine “n x n Matrix”. n bezeichnet dabei die Anzahl der Knoten im Graphen. Aus ihr kann abgelesen werden, ob innerhalb des Graphen ein Weg von einem Knoten zum anderen möglich ist. Zudem können auch die dabei entstehenden Kosten in der Adjazenzmatrix dargestellt werden.
Ihr Gegenstück ist die Inzidenzmatrix.
Adjazenzmatrix bei ungerichteten Graphen
Grundsätzlich hat eine Adjazenzmatrix den gleichen Informationsgehalt wie der dazugehörige Graph selbst. Allerdings handelt es sich um eine übersichtlichere Darstellung, die sich auch zur elektronischen Weiterverarbeitung eignet.
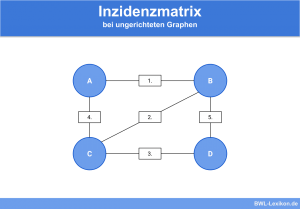
Wie eine Adjazenzmatrix bei ungerichteten Graphen aufgestellt wird, zeigen wir an folgendem Beispiel:
Anhand dieses Graphen lässt sich folgendes erkennen:
- Es existieren 4 Knoten in diesem Graphen
- Es existieren 3 Kanten in diesem Graphen
- A und B sind durch eine Kante miteinander verbunden
- A und C sind durch eine Kante miteinander verbunden
- C und D sind durch eine Kante miteinander verbunden
- B und D sind nicht durch eine Kante miteinander verbunden
Um die Adjazenzmatrix zu erstellen, bilden wir zuerst eine 4×4 Matrix, da insgesamt 4 Knoten vorhanden sind.
Damit nun die Beziehungen der Knoten untereinander in der Adjazenzmatrix dargestellt werden können, tragen wir Folgendes ein:
- existiert eine Verbindung zwischen den Knoten, wird eine “1” eingetragen
- existiert keine Verbindung zwischen den Knoten wird eine “0” eingetragen
Demnach sieht die vollständige Adjazenzmatrix unseres Graphen folgendermaßen aus:
Da es sich um einen ungerichteten Graphen handelt, können alle Kanten in beide Richtungen genutzt werden. Demnach ist die Adjazenzmatrix entlang der Diagonale von oben links nach unten rechts symmetrisch.
Adjazenzmatrix bei gerichteten Graphen
Im Gegensatz zu ungerichteten Graphen müssen bei einem gerichteten Graphen auch die Richtungen der Kanten zwischen den Knoten beachtet werden. Demnach muss die Adjazenzmatrix nicht zwingend symmetrisch sein. Es werden nur die Verbindungen zwischen den Knoten angegeben, die aufgrund der Richtung der Kanten auch miteinander verbunden werden können.
Schauen wir uns auch dies anhand eines Beispiels an.
Folgende Informationen können wir daraus entnehmen:
- Es existieren 4 Knoten in diesem Graphen
- Es existieren 5 Kanten in diesem Graphen
- A und B sind durch eine Kante miteinander verbunden
- A und C sind durch eine Kante miteinander verbunden
- B und C sind durch eine Kante miteinander verbunden
- C und D sind durch eine Kante miteinander verbunden
- D und A sind durch eine Kante miteinander verbunden
- B und D sind nicht durch eine Kante miteinander verbunden
Die sich daraus ergebende Adjazenzmatrix sieht also folgendermaßen aus:
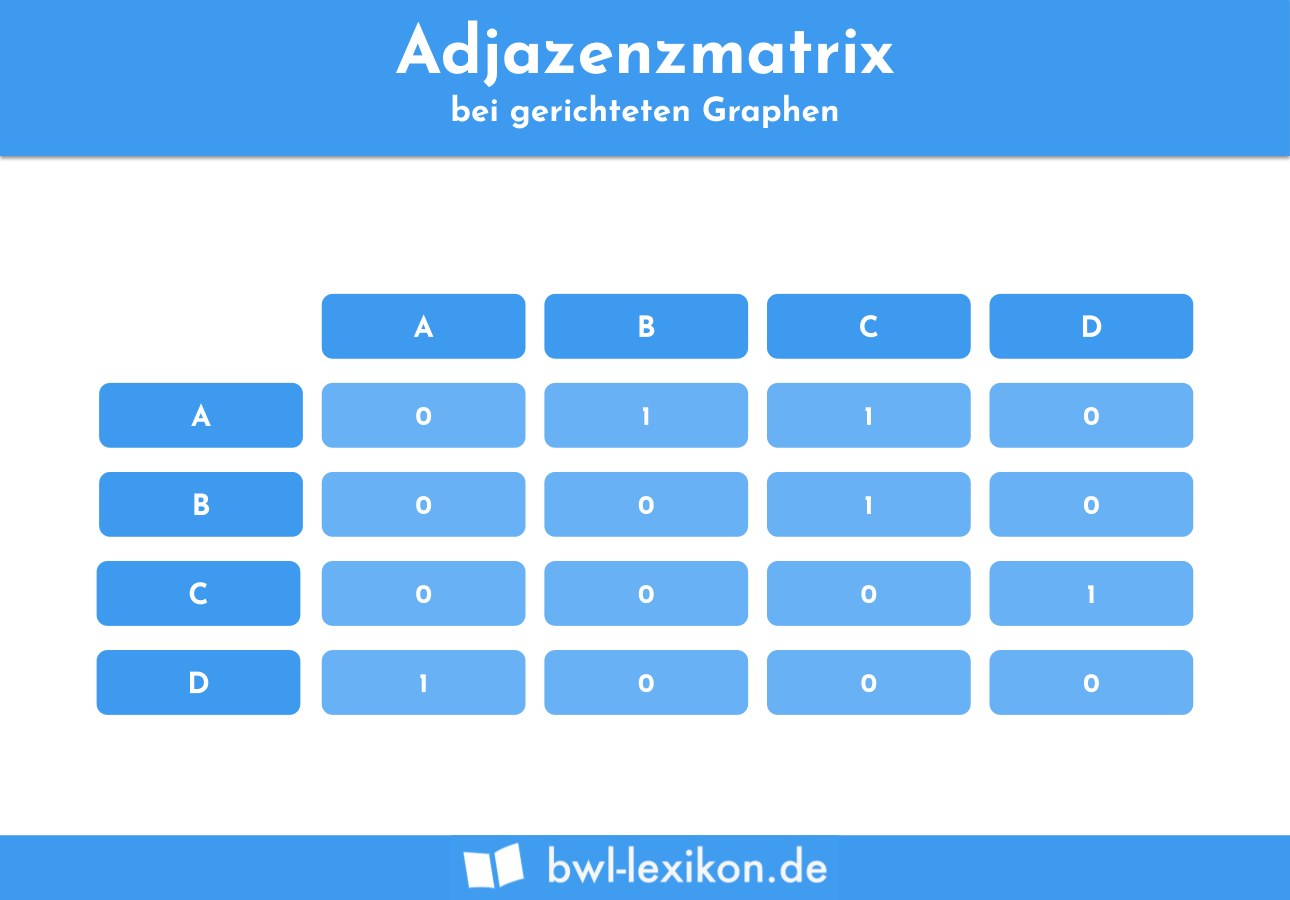
Adjazenzmatrix bei gewichteten Graphen
In gewichteten Graphen spielen die jeweiligen Kantengewichte eine wichtige Rolle. Sie beschreiben beispielsweise die Länge der Kanten oder auch die Kosten. Demnach müssen diese Kantengewichte auch in der Adjazenzmatrix dargestellt werden.
Hierfür nehmen wir einen gerichteten Graphen mit entsprechenden Kantengewichten als Beispiel:
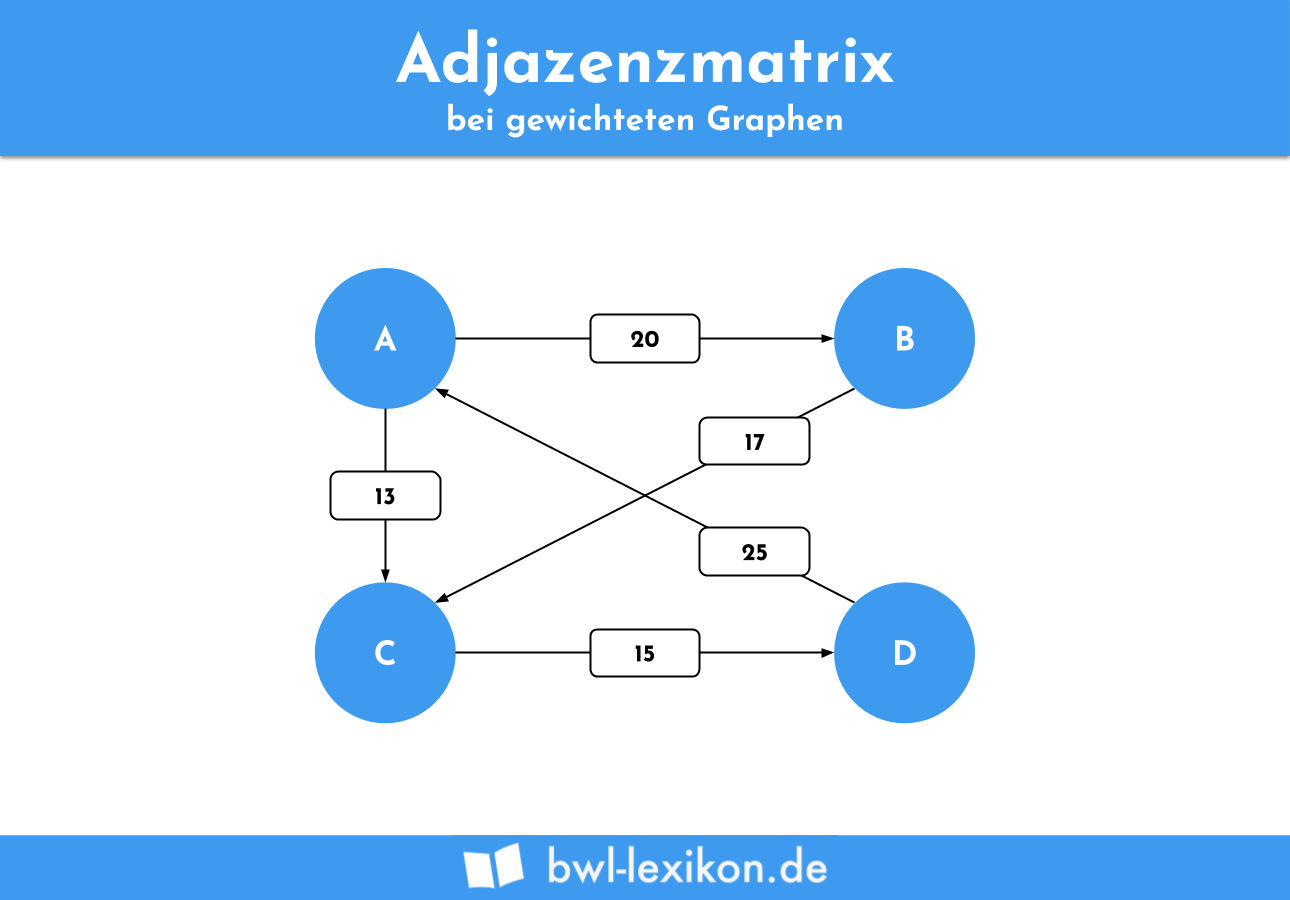
Folgende Informationen können wir daraus entnehmen:
- Es existieren 4 Knoten in diesem Graphen
- Es existieren 5 Kanten in diesem Graphen
- A und B sind durch eine Kante mit der Gewichtung 20 miteinander verbunden
- A und C sind durch eine Kante mit der Gewichtung 13 miteinander verbunden
- B und C sind durch eine Kante mit der Gewichtung 17 miteinander verbunden
- C und D sind durch eine Kante mit der Gewichtung 15 miteinander verbunden
- D und A sind durch eine Kante mit der Gewichtung 25 miteinander verbunden
- B und D sind nicht durch eine Kante miteinander verbunden
Diese Informationen möchten wir nun in der Adjazenzmatrix darstellen. Anstelle der 1 und 0 für die Existenz von Verbindungen unter den Knoten tragen wir bei gewichteten Graphen die jeweiligen Kantengewichte in die Adjazenzmatrix ein.
Dementsprechend sieht die Adjazenzmatrix für unseren Beispielgraphen folgendermaßen aus:
Weitere Form der Adjazenz-Darstellung: Die Adjazenzliste
Eine weitere Form zur Darstellung der Adjazenz von Knoten in einem Graphen ist die Adjazenzliste. Im Gegensatz zur Adjazenzmatrix ist diese etwas einfacher aufgebaut.
Für ungerichtete Graphen gilt dabei:
- Alle benachbarten Graphen werden in die Liste eingetragen.
Bei gerichteten Graphen gilt:
- Alle nachfolgenden Knoten werden in die Liste eingetragen.
Von folgendem Graphen soll eine Adjazenzliste erstellt werden:
Die Adjazenzliste zu diesem Graphen sieht folgendermaßen aus:
Anhand der Adjazenzliste erkenne wir also auf einen Blick, welche Knoten miteinander verbunden sind und welche möglichen Wege zwischen ihnen existieren.
Übungsfragen
#1. Was versteht man unter einer Adjazenzmatrix?
#2. Wozu dient eine Adjazenzmatrix?
#3. “Die Adjazenzmatrix enthält wesentlich mehr Informationen als man aus dem Graph selbst ablesen könnte.” – diese Aussage ist:
#4. “Eine Adjazenzmatrix eines ungewichteten Graphen enthält nur Nullen und Einsen zur Darstellung der Beziehungen der Knoten zueinander.” – Diese Aussage ist:
#5. “Bei einem gewichteten Graphen werden die Kantengewichte nicht in der Adjazenzmatrix aufgeführt.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
