Bipartiter Graph

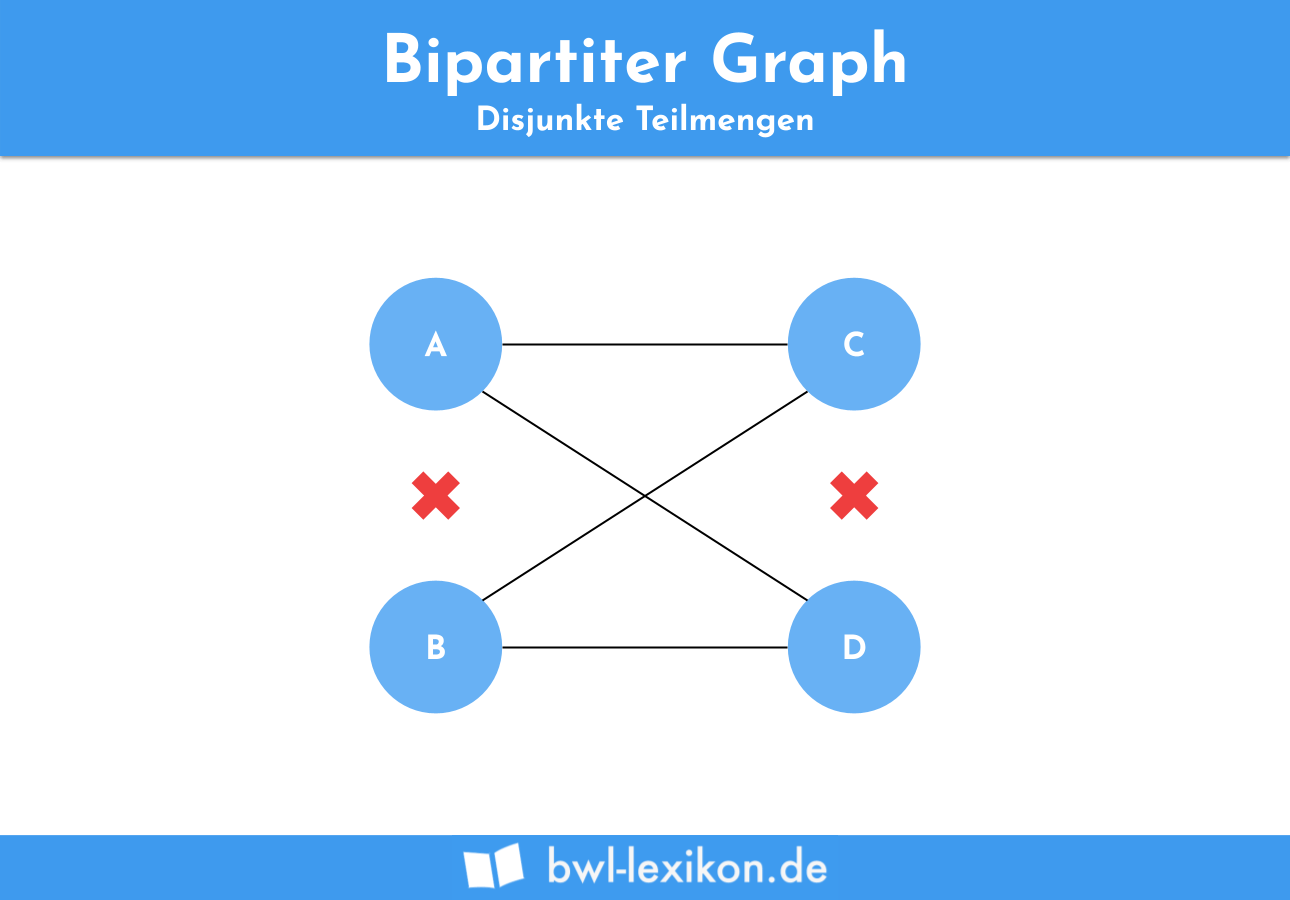
Ein Graph wird dann als bipartit bezeichnet, wenn die enthaltenen Knoten in zwei Teilmengen aufteilbar sind, deren Knoten untereinander keine verbindenden Kanten aufweisen.

Du lernst in diesem Abschnitt was man unter bipartiten Graphen versteht, warum sie wichtig sind und welche weiteren Typen von Graphen es gibt.

Synonym: paarer Graph

Warum sind bipartite Graphen wichtig?

Mit Hilfe von bipartiten Graphen lassen sich die Beziehungen der Elemente zweier Teilmengen A und B zueinander beschreiben. Mit Hilfe bipartiter Graphen können vor allem Zuordnungsprobleme bestens untersucht werden. Außerdem ist die Berechnung vieler Eigenschaften bei bipartiten Graphen mit einem geringeren Aufwand verbunden.

Was versteht man unter bipartiten Graphen?

Bipartite Graphen haben die Eigenschaft, dass sich ihre Knoten in zwei disjunkte Teilmengen (A und B) unterteilen lassen. Das bedeutet, dass unter den Knoten einer jeweiligen Teilmenge keine Kanten existieren, die die Knoten innerhalb einer Teilmenge miteinander verbinden.

Was versteht man unter bipartiten Graphen?

Bipartite Graphen haben die Eigenschaft, dass sich ihre Knoten in zwei disjunkte Teilmengen (A und B) unterteilen lassen. Das bedeutet, dass unter den Knoten einer jeweiligen Teilmenge keine Kanten existieren, die die Knoten innerhalb einer Teilmenge miteinander verbinden.

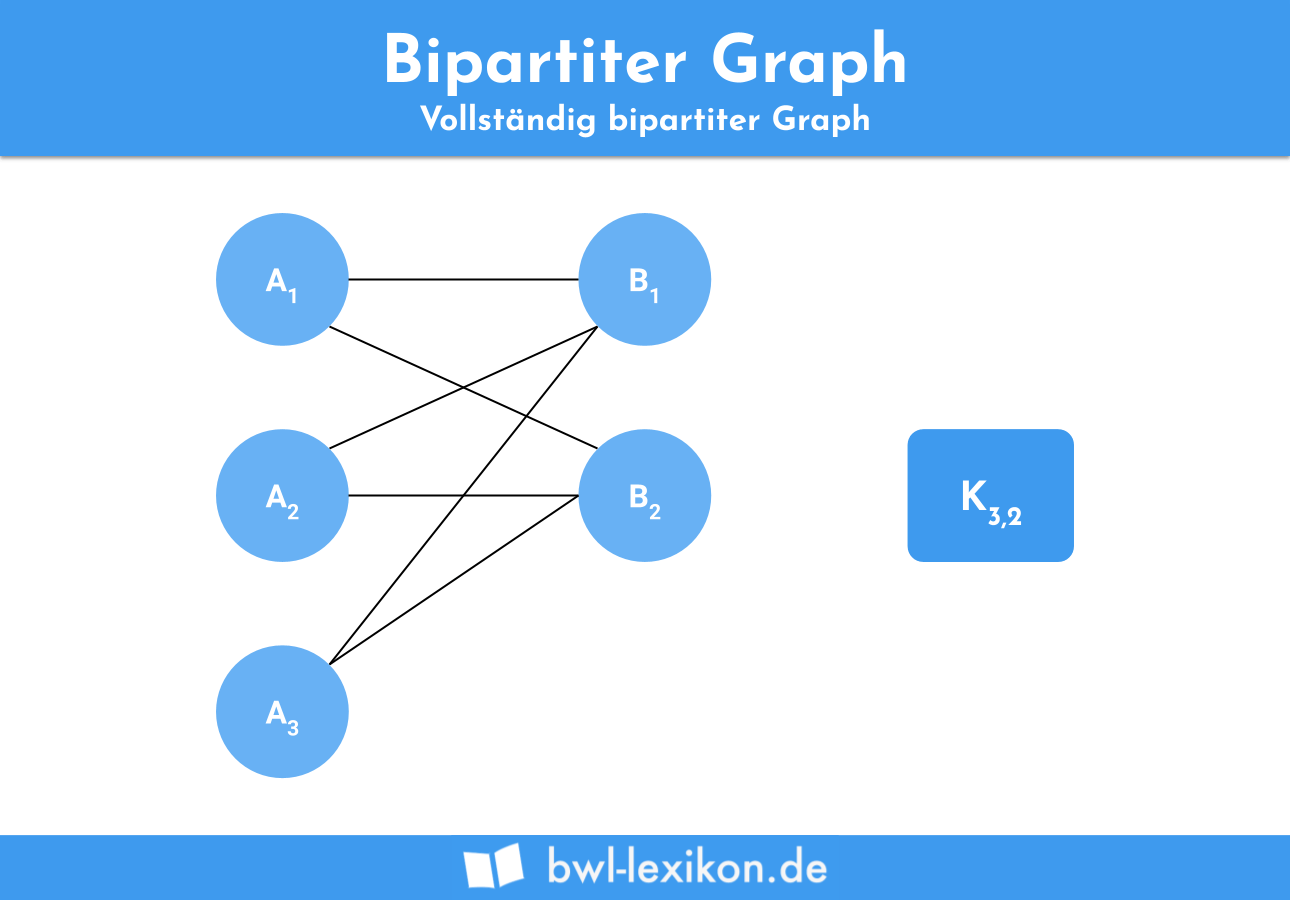
Die Teilmengen A und B der Elemente des Graphen heißen Partitionsklassen. Die Menge {A,B} wird als Bipartition des Graphen G bezeichnet.

Ist die Anzahl der Kanten im Graphen maximal, ist also jeder Knoten aus der Teilmenge A mit jedem Knoten B verbunden, so spricht man von einem vollständig bipartitem Graph. Dieser wird mit K_n,m bezeichnet. m und n bezeichnen dabei die jeweilige Anzahl der Knoten aus den Mengen A und B.

Eigenschaften bipartiter Graphen

Einen bipartiten Graph erkennt man anhand folgender Eigenschaften:

• Bei den Teilmengen A und B handelt es sich um stabile Mengen. Sie sind nicht adjazent zueinander.
• Bipartite Graphen haben ein maximales bzw. perfektes Matching.
• 2-färbbare Graphen sind bipartit, d.h. den jeweiligen Partitionsklassen können eindeutige Farben zugewiesen werden.
• Die Knotenüberdeckungszahl bipartiter Graphen ist gleich der Paarungszahl.

Weitere Typen von Graphen

Neben den bipartiten Graphen gibt es auch noch andere Typbezeichnungen für Graphen, die sich nach den jeweiligen Eigenschaften richten.

Hierzu gehören:

• Sterngraphen
• Vollständige Graphen
• Digraphen

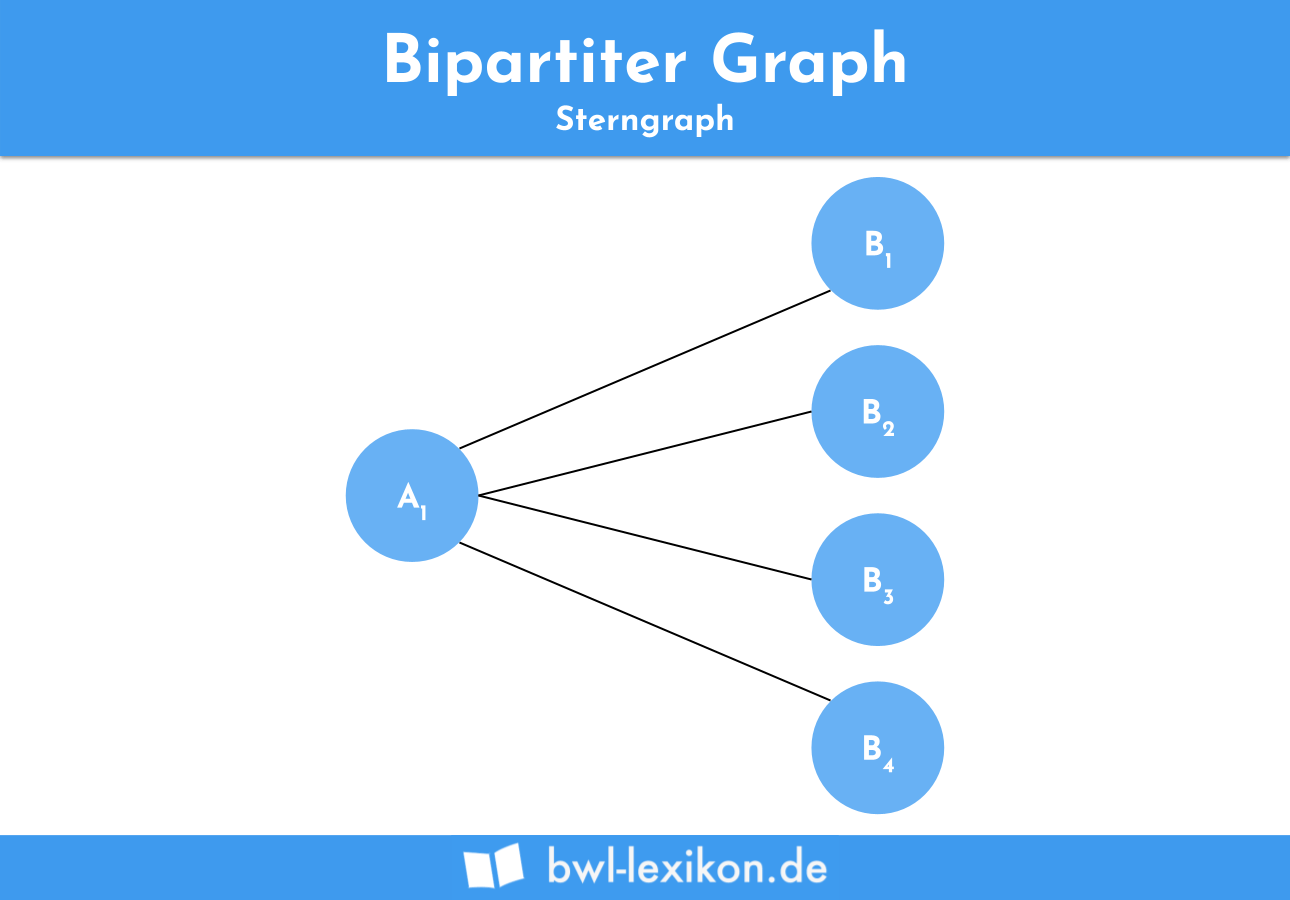
Sterngraphen

Als Sterngraph bezeichnet man einen Graphen, wenn eine der Teilmengen gleich 1 ist. Sterngraphen, die über n Kanten verfügen werden mit S_n oder auch K1,n bezeichnet.

Ein Sterngraph mit der Bezeichnung K_1,4 könnte also folgendermaßen aussehen:

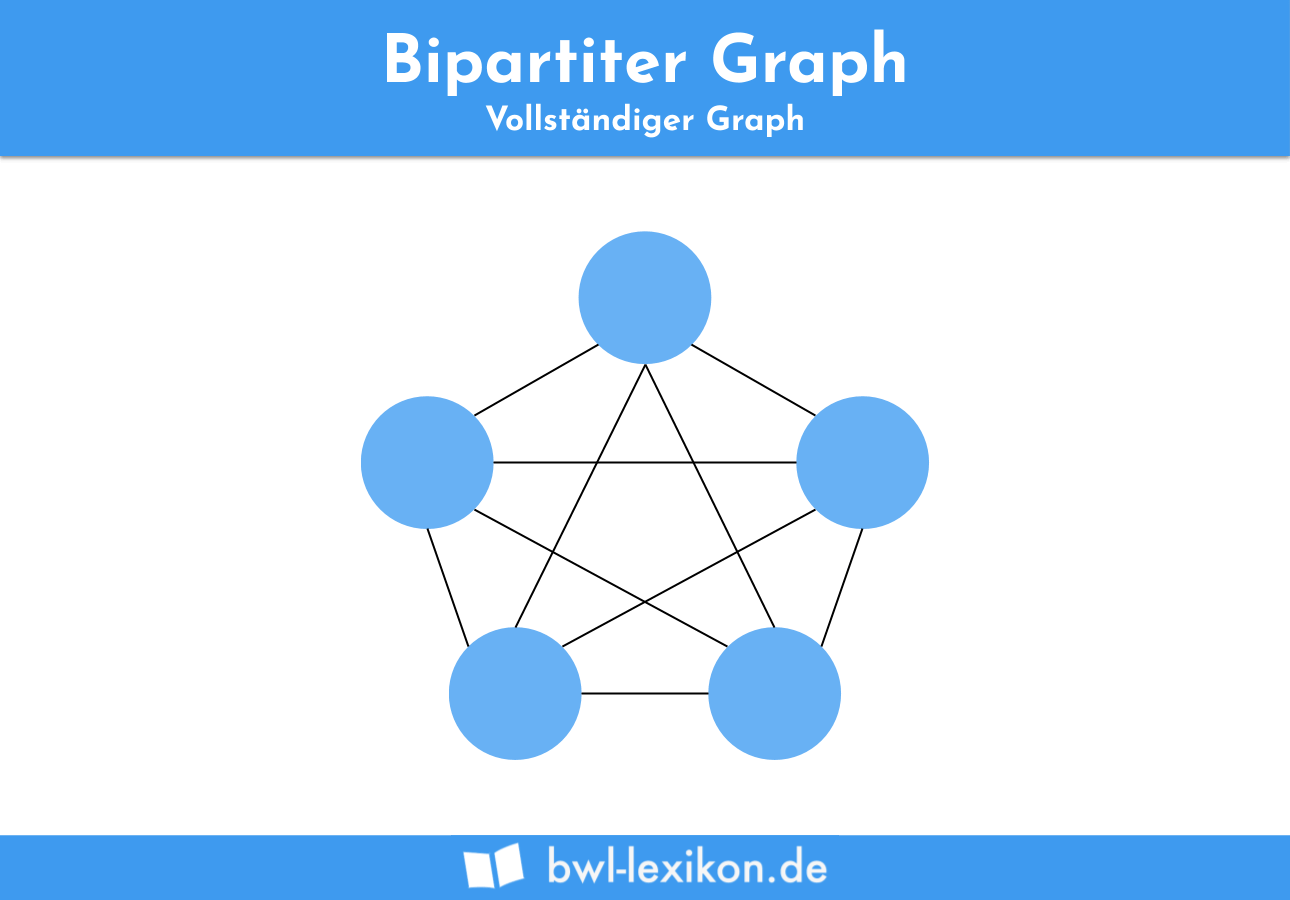
Vollständige Graphen

Vollständige Graphen haben die Eigenschaft, dass jeder Knoten n mit jedem anderen Knoten durch eine Kante verbunden ist.

Die Anzahl der Kanten in einem vollständigen Graph kann mit Hilfe der Dreieckszahl berechnet werden:

Beispiel

Der Graph G enthält fünf Knoten, die alle miteinander verbunden sind.

Eingesetzt in die Formel bedeutet das:

   

In unserem vollständigen Graph K₅ existieren also 10 Kanten.

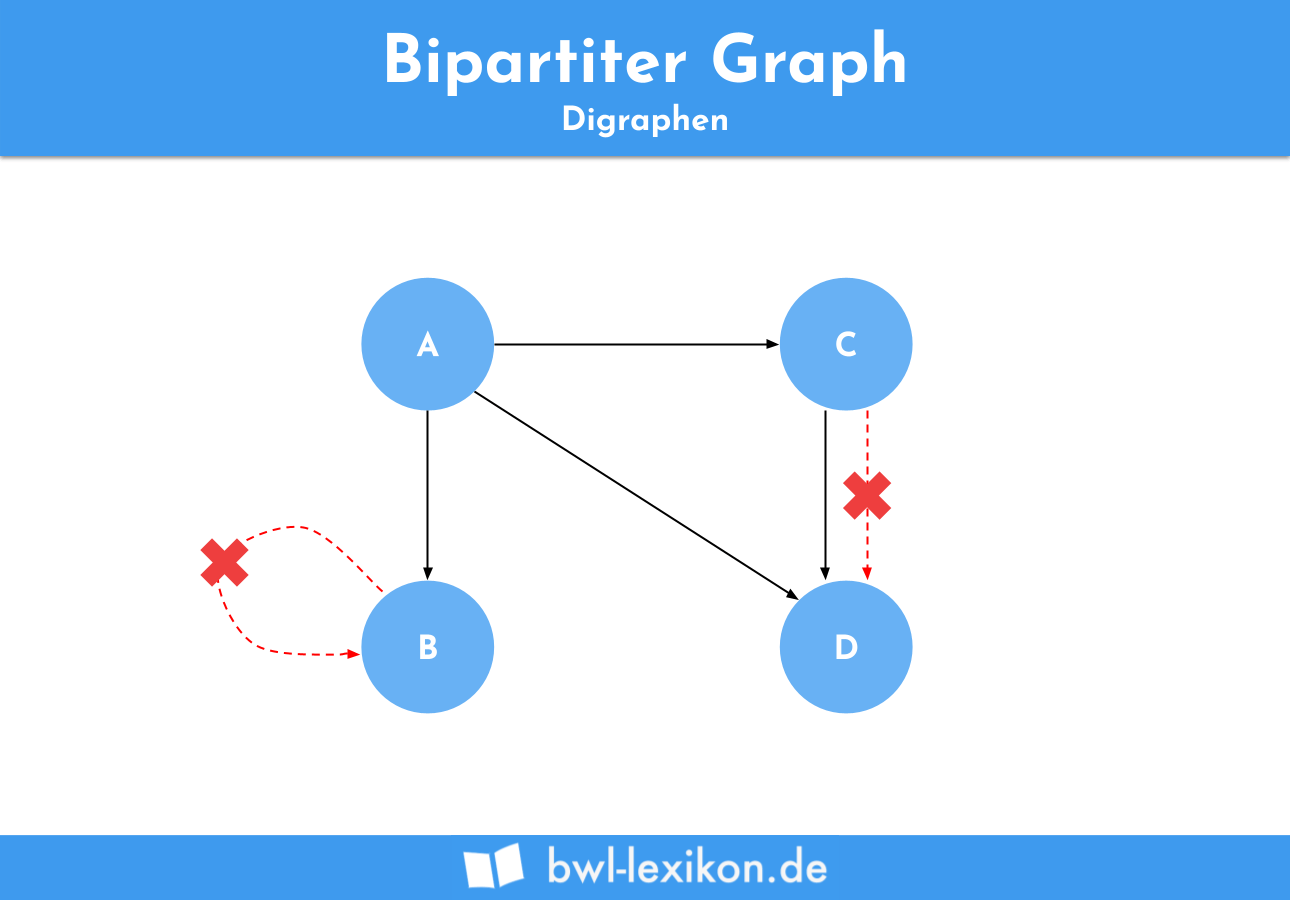
Digraphen

Ein einfacher gerichteter Graph mit einer endlichen Menge an Knoten wird als Digraph bezeichnet. Er zeichnet sich dadurch aus, dass keine parallelen Pfeile und keine Schlingen existieren.

Übungsfragen