Die Intervallskala ist eine Unterform des Skalenniveaus. Die Intervallskala kommt insbesondere bei der Erhebung statistischer Daten zur Anwendung. Sie unterstützt die Bildung von Reihenfolgen und quantifizierbaren Abständen. Neben der Intervallskala kommen im statistischen Bereich die Nominalskala, die Ordinalskala und die Verhältnisskala zum Einsatz.
In diesem Abschnitt behandeln wir das Thema Intervallskala. Du erfährst, was die Intervallskala ist und in welchen Bereichen sie eingesetzt wird. Abschließend zeigen wir dir wie sich die Intervallskala von der Nominalskala, der Ordinalskala und der Verhältnisskala unterscheidet. Zur Vertiefung deiner Kenntnisse kannst du nach dem Beitrag einige Übungsfragen beantworten.
Englisch: interval scale
Was solltest du über die Intervallskala wissen?
Die Intervallskala wird eingesetzt, um Streuungsmaße und Lageparameter zu ermitteln. Mathematische Methoden – wie z. B. die Varianz oder die Standardabweichung – können mit Unterstützung der Intervallskala leichter durchgeführt werden. Spezielle Rechenoperationen (z. B. Multiplikationen oder Divisionen) lassen sich mithilfe der Intervallskala nicht durchführen, weil bei der Intervallskala kein Nullpunkt festgelegt wird.
Wo wird die Intervallskala eingesetzt?
Die Intervallskala wird in der Meteorologie genutzt, um die Temperatur zu messen. Die Anwendung der Intervallskala bietet sich an, weil durch Minus- und Plusgrade kein Nullpunkt festgesetzt wird. Ein Meteorologe kann schnell eine Aussage darüber treffen, um wie viel Grad es heute kälter ist als gestern oder vor einer Woche. Der Intervallskala wird aber auch eingesetzt, um das Wetter für die nächsten Tage vorherzusagen. Der Meteorologe nutzt die Tatsache, dass die Abstände zwischen den einzelnen Temperaturen klar definiert sind. So kann er eindeutige Aussagen zur Wettervorhersage treffen.
Darüber hinaus misst die Intervallskala die Abstände von Daten. Ermittelst du, dass zwischen dem Jahr 2021 und dem Jahr 2015 sechs Jahre liegen, hast du die Intervallskala angewendet.
Wozu dienen Nominalskala, Ordinalskala und Verhältnisskala?
Neben der Intervallskala kommen bei Anwendung eines Skalenniveaus die folgenden Skalen zur Anwendung:
- Nominalskala
- Ordinalskala
- Verhältnisskala
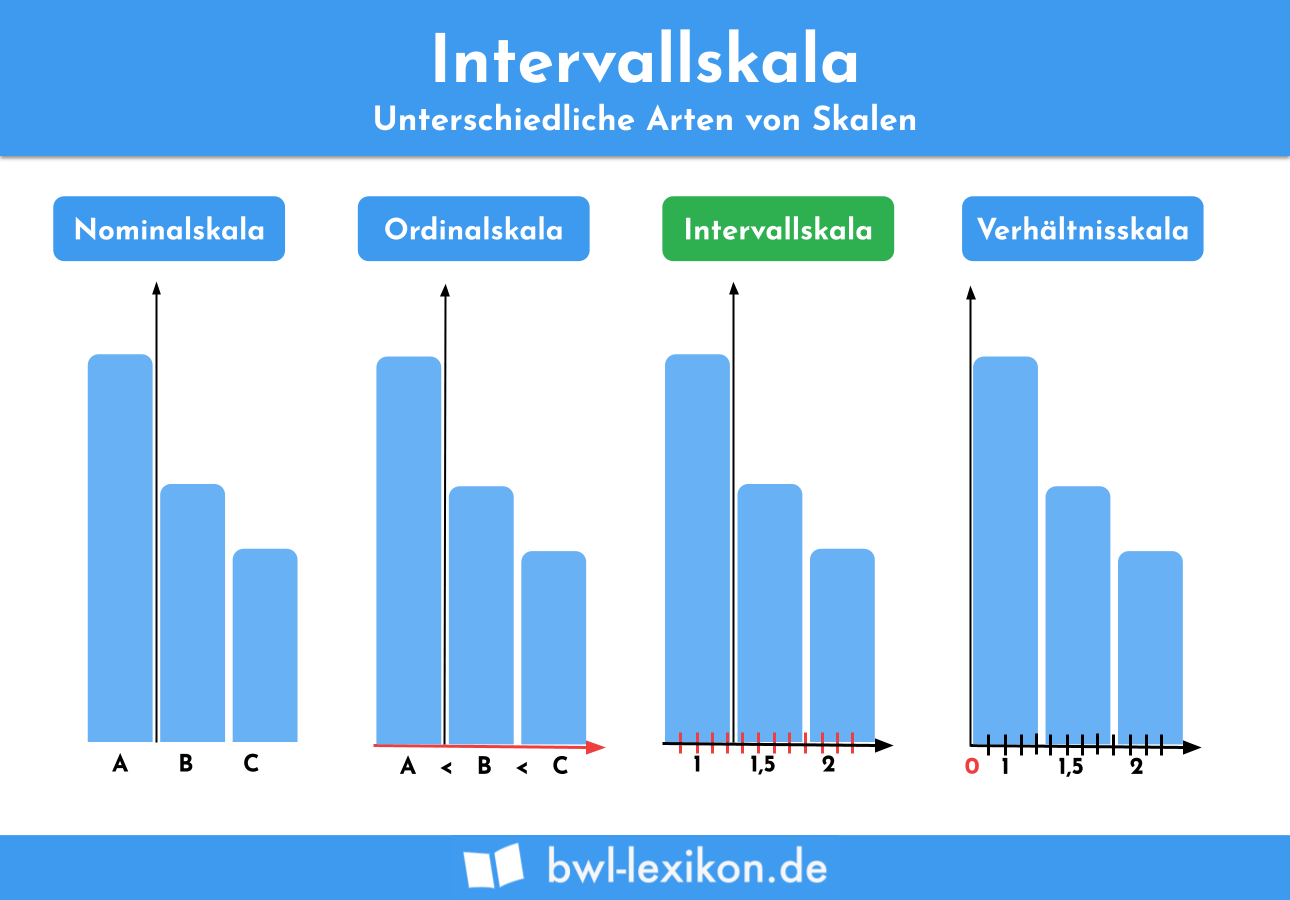
Nominalskala
Mit der Nominalskala können unterschiedliche Merkmale ermittelt werden. Die Nominalskala wird z. B. genutzt, um Menschen mit unterschiedlichen Haarfarben oder nach weiblich und männlich zu unterscheiden. Im Gegensatz zur Intervallskala eignet sich die Nominalskala nicht, um z. B. eine Rangfolge zu bestimmen. Mithilfe der Nominalskala lässt sich auch nicht feststellen, welche Fähigkeiten diese Menschen haben.
Ordinalskala
Die Ordinalskala kommt immer dort zum Einsatz, wo Variablen verwendet werden. Sie bringt diese in eine bestimmte Reihenfolge. Die einzelnen Abstände der Variablen lassen sich allerdings nicht mit Hilfe der Ordinalskala feststellen.
Verhältnisskala
Die Verhältnisskala misst, wie sich bestimmte Ergebnisse zueinander verhalten. Im Gegensatz zur Intervallskala geht die Verhältnisskala von einem Nullpunkt aus.
Unterschied zwischen Verhältnisskala und Intervallskala
Folgendes Beispiel führen dir das Verhältnis und die Unterschiede von Verhältnisskala und Intervallskala vor Augen:
Die Verhältnisskala kann nur eingesetzt werden, wenn sich ein absoluter Nullpunkt ergibt. Ist dies bei dem Marathonlauf nicht möglich – weil z. B. vergessen wurde, die Stoppuhr zu stellen – kommt die Intervallskala zum Einsatz. Hierfür ist es allerdings notwendig die Zeiten zu messen, die die Abstände zwischen den einzelnen Läufern wiedergeben. Diese Zeitdifferenzen geben die Intervalle an, die zwischen den einzelnen Läufern liegen. Mit der Intervallskala lässt sich aber nicht feststellen, um wieviel ein Läufer schnell war als sein Konkurrent.
Übungsfragen
#1. In welchem Bereich wird die Intervallskala angewendet?
#2. Was kann mithilfe der Intervallskala ermittelt werden?
#3. Welche entscheidende Größe, die z. B. bei Divisionen erforderlich ist, wird bei der Intervallskala nicht festgelegt?
#4. Wo kann die Intervallskala nicht angewendet werden?
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen