Die multiple lineare Regression ist ein Verfahren der Regressionsanalyse und stellt einen Spezialfall der linearen Regression dar. Mit Hilfe dieses statistischen Verfahrens können abhängige Variablen durch mehrere unabhängige Variablen erklärt werden.
Du wirst in diesem Abschnitt erfahren, was man unter der multiplen (linearen) Regression versteht und wozu sie angewendet werden kann. Mit Hilfe der von uns zur Verfügung gestellten Übungsaufgaben kannst du anschließend überprüfen, wie gut dein Wissen in diesem Bereich gefestigt ist.
Synonyme: lineare Mehrfachregression | mehrfache lineare Regression
Welche Bedeutung hat die multiple lineare Regression?
Die multiple lineare Regression kann als statistisches Verfahren in einer Vielzahl von Anwendungsgebieten eingesetzt werden.
Sie dient dazu, die Abhängigkeiten einer abhängigen Variablen von mehreren unabhängigen Variablen zu untersuchen. Anhand der gewonnenen Erkenntnisse können Vorhersagen und Prognosen über zukünftige Entwicklungen getroffen werden.
Dazu können im betriebswirtschaftlichen Zusammenhang beispielsweise gehören:
- Vorhersagen über die Absatzentwicklung in Abhängigkeit von Verkaufspreis und Marketingaktivität
- Prognosen zu allgemeinen Verbrauchertrends, die für die Produktentwicklung genutzt werden können.
- Die Prognosen von Besucherzahlen von Veranstaltungen in Abhängigkeit von Wetter, Eintrittspreisen und geschalteter Werbung
Was versteht man unter der multiplen linearen Regression?
Im Gegensatz zur einfachen linearen Regression wird bei der multiplen linearen Regression nicht nur der Zusammenhang von einer unabhängigen und einer abhängigen Variablen untersucht. Hierbei wird die Abhängigkeit einer abhängigen Variablen von mehreren unabhängigen Variablen betrachtet.
Beispiel zur multiplen linearen Regression
Da es eine Überraschung für sie sein soll, kann er sie leider nicht nach ihrer Ringgröße (y) fragen. Er kennt lediglich ihre Körpergröße (x1).
Um möglichst genau herauszufinden, welche Ringgröße am wahrscheinlichsten ist, befragt er 5 weitere Frauen aus seinem Umfeld ebenfalls nach der Körpergröße sowie deren Gewicht x2, dem Alter x3 und deren Ringgröße.
Aus dieser Befragung erhält er folgende Daten:
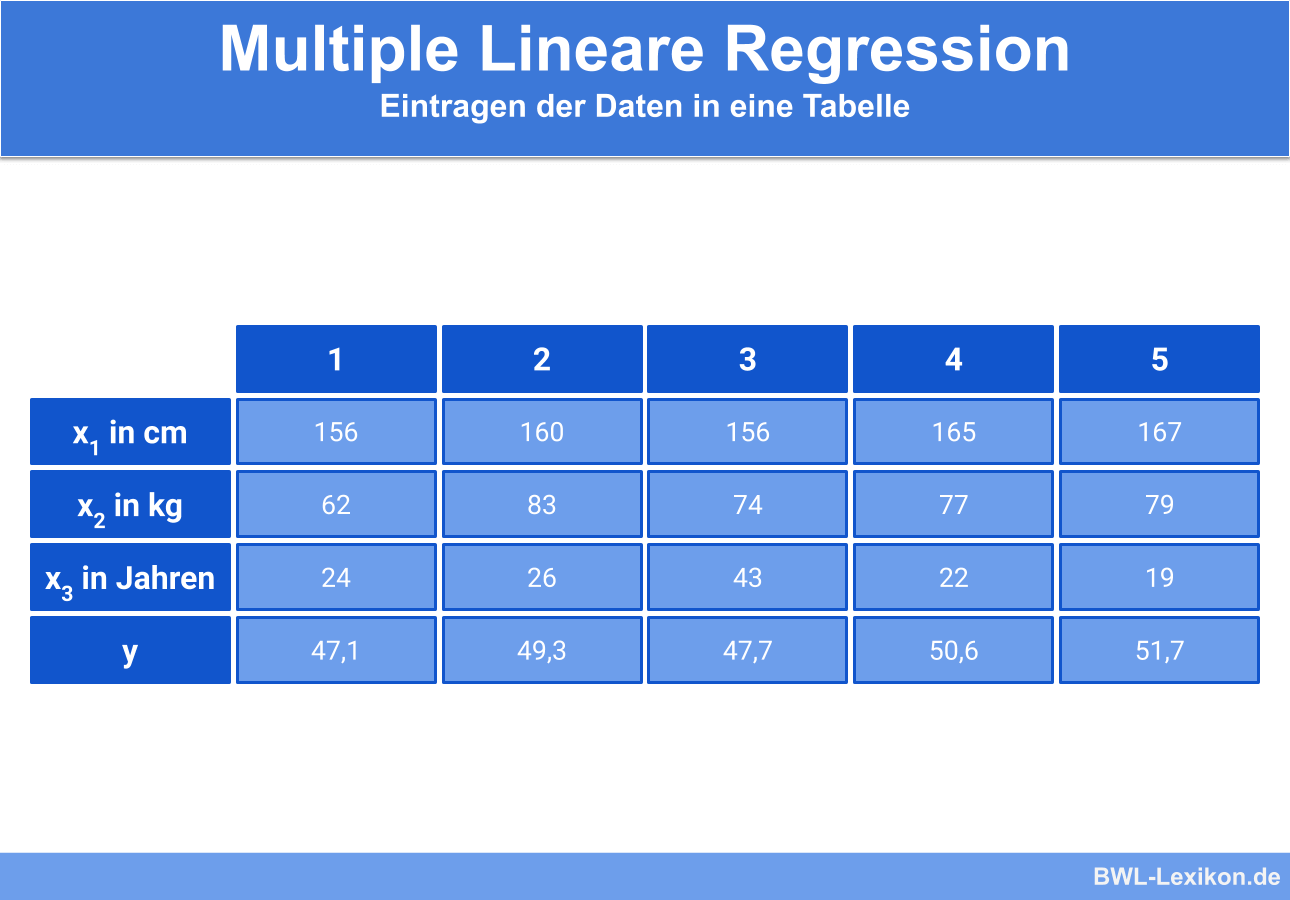
Da mehrere Einflussgrößen für die Schätzung vorhanden sind, lautet die Regressionsgleichung:
![\[ y = a+b_1x_1 + b_2x_2 + b_3x_3 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-cba2560cb6742ccaf2e008b945d31ad0_l3.png "Rendered by QuickLaTeX.com")
Mit Hilfe der multiplen linearen Regression können die Werte für a, b1, b2 und b3 ermittelt werden. Anhand derer kann anschließend eine Vorhersage getroffen werden.
Dazu werden die Parameter geschätzt, indem sie als Vektoren in einer Matrix X angesehen werden:
![\[ b = (X^TX)^{-1} X^Ty \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-9c986840668ee09211074e26314b7329_l3.png "Rendered by QuickLaTeX.com")
Diese Operationen werden zumeist mit einer speziellen Berechnungssoftware gelöst, da die Berechnung per Hand äußerst kompliziert und aufwendig ist.
Dabei entstehen folgende Werte für die einzelnen Parameter:
- a = 0,6
- b1 = 0,28
- b2 = 0,06
- b3 = -0,02
Als Regressionsgerade erhalten wir folgende Funktion:
![\[ y = 0,66 + 0,28x_1 + 0,6x_2 - 0,02x_3 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-b77f01e38a707b4fc6a2935f4d658a0b_l3.png "Rendered by QuickLaTeX.com")
Anschließend können diese Parameter interpretiert werden:
So bedeutet b1 = 0,28 beispielsweise, dass je Zentimeter Körpergröße die Ringgröße um 0,28 steigt. Damit besteht zwischen den Einflussgrößen ein positiver Effekt.
Als Schlussfolgerung daraus führt eine größere Körpergröße auch zu einer größeren Ringgröße. Beim Parameter Alter hingegen ist es umgekehrt. Hier besteht ein negativer Effekt, da b3 = -0,2 besagt, dass pro Lebensjahr die Ringgröße um 0,02 abnimmt.
Da der Wert sehr nahe bei Null liegt und die gemachten Stichproben nur in recht geringerer Anzahl vorhanden sind, kann in diesem Zusammenhang sogar davon ausgegangen werden, dass das Alter nur einen sehr geringen, wenn sogar gar keinen Effekt auf die Ringgröße hat. Um dies zu bestätigen, kann die Signifikanz überprüft werden.
Anhand der gewonnenen Werte und der ermittelten Funktion für die Regressionsgerade kann Herr Müller nun die Ringgröße seiner Freundin schätzen. Er weiß, dass sie 170cm groß ist, 29 Jahre alt und 68 kg wiegt.
Diese Werte werden in die Funktion der Regressionsgeraden eingesetzt, um die Ringgröße (y) der Freundin vorherzusagen:
![\[ y = 0,66 + (0,28*170) + (0,06*68) - (0,02*29) = 51,76 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-53f8c15bfe3721d7d8daf8e61809bd9b_l3.png "Rendered by QuickLaTeX.com")
Die wahrscheinlichste Ringgröße für die Freundin von Herrn Müller liegt also bei 51,76. Er bestellt also einen Ring in dieser Größe, um seine Freundin zu überraschen.
Übungsfragen
#1. Was versteht man unter der multiplen (linearen) Regression?
#2. Wozu kann das Verfahren der multiplen linearen Regression im betriebswirtschaftlichen Zusammenhang genutzt werden?
#3. “Mit der multiplen linearen Regression können die Auswirkungen mehrerer Einflussgrößen auf eine Zielgröße untersucht werden.” – Diese Aussage ist:
#4. “Die multiple lineare Regression kann sehr einfach durchgeführt werden und benötigt keinerlei zusätzlicher Berechnungssoftware.” – Diese Aussage ist:
#5. “Besteht ein negativer Effekt zwischen zwei Variablen, bedeutet das, dass wenn die eine variable steigt, auch die abhängige Variable steigt.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
