Stichprobenumfang

Enthält: Beispiele · Definition · Formeln · Grafiken · Übungsfragen

Der Stichprobenumfang gibt an, wie groß eine Stichprobe sein muss, damit ausreichend sichere Ergebnisse und Aussagen im Hinblick auf die Grundgesamtheit der untersuchten Datenreihe getroffen werden können.

Du wirst in diesem Kapitel lernen, welche Bedeutung der Stichprobenumfang hat und was man genau darunter versteht. Wir zeigen dir wie der Stichprobenumfang berechnet wird und stellen dir einige Übungsaufgaben am Ende dieses Kapitels zur Verfügung, mit denen du dein Wissen testen kannst.

Englisch: sample size

Welche Bedeutung hat der Stichprobenumfang?

Werden Datenreihen in Form von Stichproben untersucht, so sollen dadurch Aussagen und Ergebnisse gewonnen werden, die sich auf die Gesamtheit der Datenreihe übertragen lassen. Um diese zu erhalten, muss die untersuchte Stichprobe ausreichend groß sein. Der Stichprobenumfang gibt genau diese Größe an. Zu wissen, wie groß eine zu untersuchende Stichprobe sein muss ist eine wesentliche Grundlage, um Aussagen in der Statistik treffen zu können.

Was versteht man unter dem Stichprobenumfang?

Der Stichprobenumfang gibt die mindestens erforderliche mengenmäßige Größe einer Stichprobe an, um anhand dieser Aussagen bezüglich der Gesamtheit der untersuchten Werte treffen zu können.

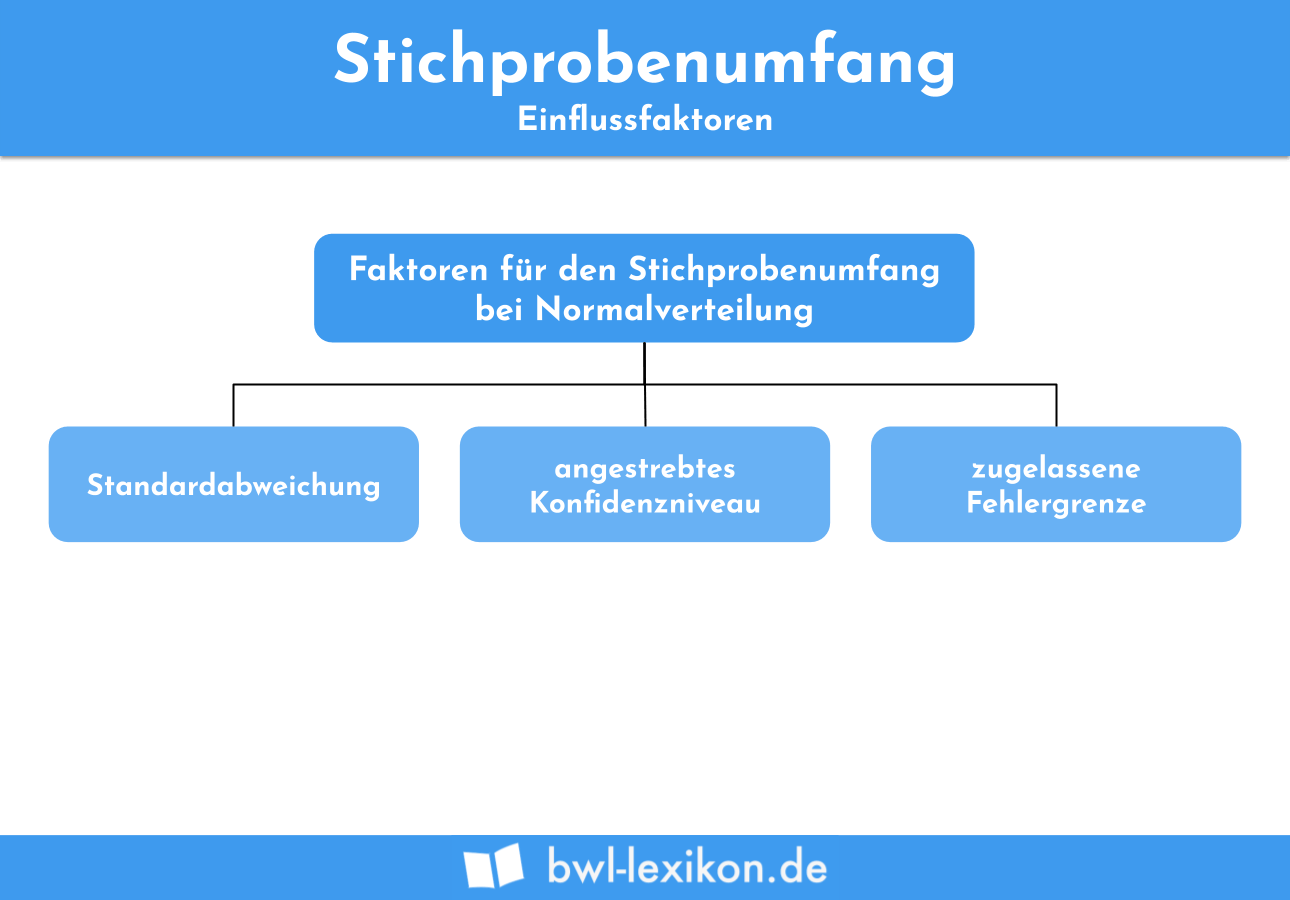
Sofern eine Normalverteilung vorliegt, hängt der Stichprobenumfang von drei wesentlichen Faktoren ab:

  • der Standardabweichung
  • dem angestrebten Konfidenzniveau
  • der zugelassenen Fehlergrenze
Stichprobenumfang: Einflussfaktoren
Stichprobenumfang: Einflussfaktoren

Was ist das Konfidenzniveau?

Das Konfidenzniveau muss bei einer statistischen Erhebung festgelegt werden. Es gibt die Wahrscheinlichkeit an, mit der die Lageschätzung eines statistischen Wertes (zum Beispiel des Mittelwerts) aus einer Stichprobe auch auf die Grundgesamtheit der untersuchten Werte zutrifft. Ein Konfidenzniveau von 90 Prozent bedeutet also, dass mit 90 prozentiger Wahrscheinlichkeit beispielsweise der Mittelwert einer Stichprobe auch dem Mittelwert der Grundgesamtheit entspricht.

Je höher das Konfidenzniveau und damit die gewünschte Sicherheit liegen soll desto größer muss der Stichprobenumfang sein. In der Berechnung des Stichprobenumfangs wird die Aussagewahrscheinlichkeit, mit dem sogenannten z-Wert angegeben. Liegt eine Normalverteilung vor, so kann dieser aus einer z-Wert-Tabelle entnommen werden.

Ausgewählte z-Werte bei häufig vorkommenden Aussagewahrscheinlichkeiten sind:

Aussagewahrscheinlichkeit50 %75 %95 %99 %
Z-Wert0,6741,151,962,57

Berechnung des Stichprobenumfangs

Für die Berechnung des Stichprobenumfangs sind folgende Schritte notwendig:

  1. Festlegung der absoluten Genauigkeit
    Die geforderte absolute Genauigkeit (e) muss festgelegt werden. Darunter versteht man die maximal zulässige Abweichung des durch die Stichprobe ermittelten Wertes gegenüber dem Wert der Grundgesamtheit
  2. Schätzung der Standardabweichung
    Die Standardabweichung (s) gibt die Streuung der betrachteten Einzelwerte an um den Mittelwert an. Berechnet werden kann diese erst nach Durchführung der Stichprobe, weshalb sie zur Berechnung des Stichprobenumfangs geschätzt werden muss. Das kann mit folgender Faustformel geschehen:

        \[ s \approx \frac{x_{max}-x_{min}}{3,5} \]

  3. Festlegen der Aussagenwahrscheinlichkeit (Konfidenzniveau)
    Die gewünschte Aussagenwahrscheinlichkeit wird festgelegt und der zugehörige z-Wert ermittelt.
  4. Berechnung des Stichprobenumfangs
    Sind alle erforderlichen Werte ermittelt, so kann der Stichprobenumfang (n)berechnet werden, welcher aus der Grundgesamtheit (N) gewählt werden sollte. Dazu werden die zuvor ermittelten Werte in die entsprechende Formel eingesetzt:

    • bei einer endlichen Grundgesamtheit:

          \[ $n \geq \ \frac{N * z^{2}*s^{2}}{z^{2}*s^_{2} + (N-1) * e^{2}} \]

    • bei einer unendlichen Grundgesamtheit:

          \[ $n \geq \ \frac{z^{2}*s^{2}}{e^{2}} \]

Statistisch gesehen muss der Stichprobenumfang mindestens n betragen. In der Praxis sollte in vielen Werten ein etwas höherer Wert genommen werden. So können weitere Faktoren berücksichtigt werden, beispielsweise fehlerhaft ausgefüllte Fragebogen bei Befragungen.

Beispiel zur Berechnung des Stichprobenumfangs
Die „Stich&Prob AG möchte die mittlere Bearbeitungszeit eines Herstellungsprozesses einer ihrer Produkte anhand einer Stichprobe ermitteln. Es ist bekannt, dass dieser Prozess 100 mal im Monat durchgeführt wird. Bisher wurde die nötige Bearbeitungszeit noch nicht erhoben, weshalb die mittlere Bearbeitungszeit zunächst auf 60 Minuten und die Standardabweichung der Bearbeitungszeit auf 10 Minuten geschätzt wird. Die maximale Abweichung der in der Stichprobe ermittelten Werte vom Wert der Grundgesamtheit soll höchstens 5 Prozent betragen.

Um den nötigen Umfang der Stichprobe zu ermitteln wird folgendermaßen vorgegangen:

  1. Festlegung der absoluten Genauigkeit
    Da die relative Genauigkeit erel 5 Prozent betragen soll, kann die absolute Genauigkeit wie folgt ermittelt werden:

        \[ e = 0,05 * 60~min = 3~min \]

  2. Schätzung der Standardabweichung
    Die Standardabweichung der Bearbeitungszeit wird auf 10 Minuten geschätzt

        \[ s = 10 min \]

  3. Festlegen der Aussagenwahrscheinlichkeit (Konfidenzniveau)
    Die gewünschte Aussagenwahrscheinlichkeit soll 95 Prozent betragen. Der dazugehörige z-Wert ist:

        \[ z = 1,96 \]

  4. Berechnung des Stichprobenumfangs
    Der Stichprobenumfang kann nun mit der entsprechenden Formel berechnet werden:

        \[$n \geq \ \frac{N * z^{2}*s^{2}}{z^{2}*s^_{2} + (N-1) * e^{2}} \]

        \[ $n \geq \ \frac{100 * 1,96^{2}*10^{2}}{1,96^{2}*10^_{2} + (100-1) * 3^{2}} \]

        \[ $n \geq \ 30,12 \]

Rein statistisch müsste der Stichprobenumfang also mindestens 31 (wird immer aufgerundet) betragen, um ein aussagekräftiges Ergebnis im Hinblick auf die mittlere Bearbeitungszeit zu erhalten.

Übungsfragen

#1. Was versteht man unter einer dem Stichprobenumfang?

#2. Der Stichprobenumfang ist maßgeblich abhängig von:

#3. “Da die Standardabweichung vor der Durchführung der Stichprobe noch nicht bekannt ist, muss sie zunächst geschätzt werden.” - Diese Aussage ist:

#4. “Der Stichprobenumfang variiert stark in Abhängigkeit von der gewünschten Genauigkeit der Ergebnisse.” - Diese Aussage ist:

#5. “Der benötigte Z-Wert zur Berechnung des Stichprobenumfangs muss zunächst immer wieder aufs Neue aufwendig berechnet werden.” - diese Aussage ist:

Fertig

Ergebnis

Könnte dich auch interessieren:

Nichts passendes dabei?

Erkunde andere Fachbereiche oder benutze die Suchfunktion. Falls Du keine Antwort auf Deine Frage findest, schick uns gerne eine Nachricht, wir versuchen dann passenden Content für Dich zu schaffen.

Zur Übersicht
Oder lieber die Suche benutzen?