In dieser Lektion dreht sich alles um die Variablen im Fachbereich Statistik. Du erfährst, was Variablen genau sind, wie sie sich einteilen lassen, wie sie gemessen werden und welche Skalen es für die Messung gibt. Zum Schluss stellen wir dir einige Übungsfragen zur Verfügung, damit du deinen Lernstand kontrollieren kannst.
Einteilung der Variablen
In der Statistik finden sich sehr unterschiedliche Arten von Variablen.
Sie werden zum Beispiel unterteilt in:
- quantitative und qualitative Variablen
- stetige und diskrete Variablen
- manifeste und latente Variablen
- abhängige und unabhängige Variablen
Quantitative und qualitative Variablen
Quantitative Variablen sind metrisch, kontinuierlich und skaliert. Sämtliche Werte werden in Zahlen dargestellt und geben Informationen über die Ausprägungen einer Größe. Diese Informationen ermöglichen auch Aussagen über die Abstände zwischen den Ausprägungen, beispielsweise die Größe eines Objekts und die Beantwortung der Frage, welches Objekt oder welche Person am größten, am kleinsten etc. ist.
Qualitative Variablen informieren über die Zugehörigkeit eines Objektes oder einer Person zu einer Kategorie. Deren Ausprägungen werden in der Regel nicht in Zahlen, sondern in Buchstaben wiedergegeben.
Sind exakt zwei Ausprägungen möglich, wird auch von einer binären oder dichotomen Variablen gesprochen, beispielsweise
- schwanger / nicht schwanger
- lebendig / tot
Stetige und diskrete Variablen
Stetige Variablen lassen sich beliebig exakt beschreiben, die Anzahl der möglichen Werte ist unendlich. Aufgrund einer derart genauen Messung kommt es nicht mehr vor, dass mehrere Merkmalsträger dieselbe Ausprägung besitzen. So lässt sich beispielsweise die Zeit in unendlich kleinen Einheiten wie Milli- und Nanosekunden ausdrücken; gleiches gilt für Temperaturen, Gewichte, Größen und vieles mehr.
Diskrete Variablen dagegen sind endlich innerhalb eines beliebigen Intervalls und somit exakt abzählbar. Sie lassen sich nicht genauer bestimmen, denn die Einheiten, in denen sich die Ausprägungen der Merkmale bestimmen lassen, sind fest.
Typisch für diskrete Variablen sind Anzahlen, beispielsweise von Kunden in einer bestimmten Filiale oder von Parkplätzen eines Supermarktes. Auch Schulnoten, Augenzahlen auf Würfeln oder das Alter in Jahren fallen in diese Kategorie.
Manifeste und latente Variablen
Bei manifesten Variablen handelt es sich um Merkmale, die direkt gemessen oder beobachtet werden können. Sie lassen keinen Spielraum für Interpretationen zu. Das heißt, das Merkmal ist objektiv festgelegt und damit eindeutig.
Beispiele für manifeste Variablen sind Geschlecht, Gewicht, Anzahl der Filialen einer Fastfood-Kette, Wohnort etc.
Latente Variablen können nur indirekt erfasst werden und ergeben sich aus dem Rückschluss aus manifesten Variablen. Dazu müssen geeignete manifeste Variablen ausgewählt werden, um ein Kontrukt messen zu können. Dieser Prozess nennt sich Operationalisierung. Die Herausforderung besteht darin, dass es für jede latente Variable verschiedene manifeste Variablen gibt.
Ein Beispiel ist die Zufriedenheit der Leser mit einem bestimmten Buch, die unter anderem messbar ist mittels Umfragen, Anzahl der verkauften Exemplare, Likes in sozialen Medien, Rezensionen, Bewertungen in Online-Shops und vielem mehr.
Abhängige und unabhängige Variablen
Die Frage, ob eine Variable abhängig oder unabhängig ist, wird vor allem in der hypothesenprüfenden Forschung gestellt, beispielsweise im Zuge von Experimenten. Die Einordnung der Variablen in „abhängig“ oder „unabhängig“ basiert auf dem jeweiligen Kontext der Untersuchung und dem Versuchsaufbau. Dasselbe Merkmal kann also je nach Experiment sowohl abhängig als auch unabhängig sein.
Eine unabhängige Variable wird im Rahmen eines Experiments verändert bzw. variiert, damit ihre Auswirkung auf die abhängige Variable erfasst werden kann. Die unabhängige Variable nimmt also einen möglichen Einfluss auf die abhängige Variable. Gemessen wird die Veränderung der abhängigen Variablen infolge dieses Einflusses.
Beispiel: Wie verändert sich die Konzentrationsfähigkeit der Studierenden (abhängige Variable), wenn sich die Temperatur im Raum (unabhängige Variable) erhöht oder verringert?
Messung der Variablen
Im Zuge einer Messung geht es um den Versuch, einen Ausschnitt der Realität in Messwerten, also in Zahlen darzustellen. Dabei werden die Zahlen den Merkmalsträgern zugeordnet, und zwar auf Grundlage ihrer Ausprägungen mittels definierter Regeln.
So wird zum Beispiel die Körpergröße in Zentimeter, eine Schulleistung in Noten und eine Zeit in Sekunden dargestellt.
Die Definition, wie die Zahlen den Merkmalsträgern zugeordnet werden, erfolgt über eine Skala. Die möglichen Ausprägungen werden auch als „Skalierung“ bezeichnet.
Folgende Mindestvoraussetzungen müssen erfüllt sein:
- Exklusivität: Verschiedene Ausprägungen der Merkmale werden verschiedenen Zahlen zugordnet.
Es existiert eine umfängliche und komplexe Definition für das Messen.
Sie lautet:
„Messen ist eine Zuordnung von Zahlen zu Objekten oder Ereignissen, sofern diese Zuordnung eine homomorphe Abbildung eines empirischen Relativs in ein numerisches Relativ ist.“
– Orth, Bernhard (1983): Grundlagen des Messens. In: Feger, H. et al. (Hg.): Messen und Testen. Göttingen. S. 136 – 180 –
Bei einer homomorphen Abbildung handelt es sich um eine eindeutige und nicht umkehrbare Abbildung dessen, was gesehen oder beobachtet wird, in eine Zahl. Homomorph bedeutet, dass die Relationen Zahlen dem numerischen Verhältnis den Relationen der Objekte entsprechen.
Beispiel: Michael ist sichtlich größer als Martina, also sollte ihm eine größere Zahl zugeordnet werden als Martina.
Es existieren theoretisch viele unterschiedliche Möglichkeiten, wie die entsprechende Skala aussehen könnte. In Deutschland wird beispielsweise in Metern und/oder Zentimetern gemessen, in den USA dagegen in Foot und/oder Inch. Doch auch eine einfache Skalierung wie Michael = 2 und Martina = 1 würde die Bedingungen erfüllen, da 2 >1.
Entwicklung messbarer Skalen
Im Zuge der Erstellung bzw. Entwicklung messbarer Skalen sind einige Punkte zu beachten:
- das Problem der Repräsentation
- das Problem der Eindeutigkeit
- das Problem der Bedeutsamkeit
Repräsentationsproblem
Die empirischen Objektrelationen sind durch Zahlenrelationen darzustellen, die wiederum den Objekten zuzuordnen sind.
Beispiel: Martina < Michael; 1 < 2
Eindeutigkeitsproblem
Die Zuordnungsregeln müssen eindeutig festgelegt werden.
Beispiel: Ergänzung einer Skala um eine Zahl, Umrechnung von Zentimeter in Millimeter
Bedeutsamkeitsproblem
Welchen Nutzen liefern die mit den Messungen verbundenen numerischen Aussagen?
Beispiel: Können sinnvolle Durchschnittswerte ermittelt werden?
Um diese Probleme zu lösen, wurde von Stevens im Jahr 1946 das Konzept der vier Skalenniveaus entwickelt (S. S. Stevens: On the Theory of Scales of Measurement. In: Science. 1946, 103, S. 677–680). Das Konzept wird nach wie vor in sämtlichen anerkannten Lehrbüchern zum Thema Statistik sowie in verbreiteten Statistik-Programmen verwendet.
Die vier Skalenniveaus nach Stevens
Stevens unterscheidet die vier Skalenniveaus
- Nominalskala
- Ordinalskala
- Intervallskala
- Ratioskala bzw. Verhältnisskala
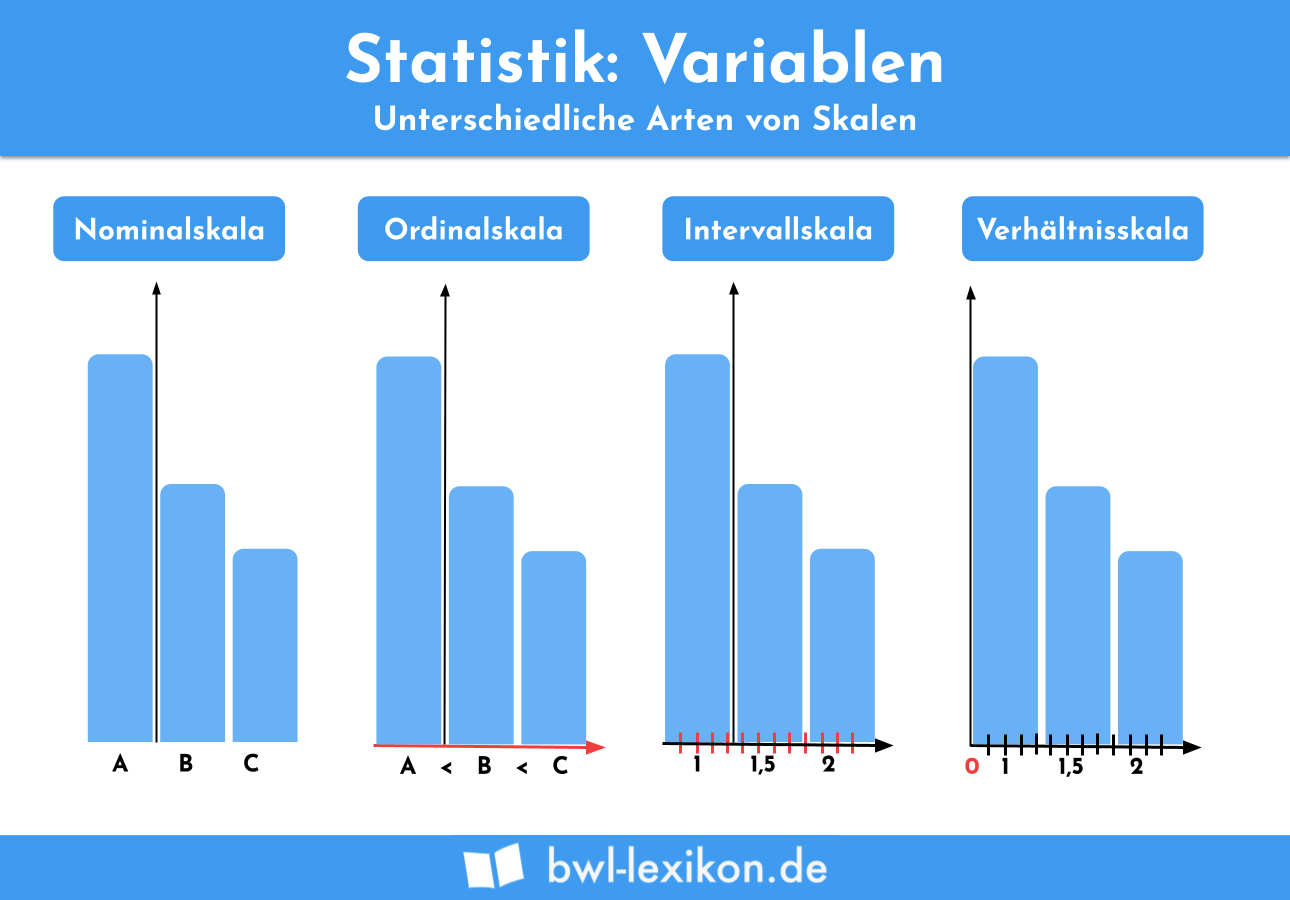
Sowohl in der Praxis als auch in Statistik-Softwareprogrammen werden in der Regel das Intervall- und das Verhältnisskalenniveau zusammengefasst; ihre Bezeichnung lautet dann „metrisch“ oder „parametrisch“. Der Grund für die Zusammenfassung besteht einfach darin, dass die Unterscheidung der beiden Skalen weniger von praktischem, sondern vielmehr von theoretischem Interesse ist.
Nominalskala
Weisen die Merkmale von Objekten die gleiche Ausprägung auf, erhalten sie gleiche Zahlen. Sind die Merkmalsausprägungen unterschiedlich, erhalten sie unterschiedliche Zahlen.
Die Interpretation lautet schlicht „ist gleich“ oder „ist nicht gleich“. Das heißt, dass die Ausprägungen der Merkmale lediglich daraufhin verglichen werden, ob sie übereinstimmen oder nicht.
Die Relation wird definiert als = und ≠
Aussagekraft
Hinsichtlich der Nominalskala erlauben die Zahlen nur eine Aussage darüber, ob ein Objekt bzw. Merkmalsträger die gleiche Eigenschaft besitzt wie eine oder mehrere andere. Eine Bewertung ist nicht möglich. So hat eine Person beispielsweise blonde Haare, eine zweite braune. Die Farben sind nicht gleich. Eine Bewertung nach dem Muster „x < y“, also „blond < braun“ oder umgekehrt ist in diesem Fall nicht umsetzbar.
Die Nominalskala eignet sich zum Beispiel für
- Wohnorte
- Bundesländer
- Geschlecht
- Familienstand
- Abteilungszugehörigkeit
Ordinalskala
Die Ordinalskala wird auch als Rangskala bezeichnet. Objekten mit einer größeren Merkmalsausprägung werden höhere Zahlen zugeordnet als denen mit kleinerer Ausprägung. Auch der umgekehrte Fall ist möglich. Eine Aussage zu den Wertabständen (um wie viel höher ist Wert x als y?) ist allerdings nicht möglich.
Die Rangfolgen können gebildet werden mittels = und ≠ sowie < und >.
Rangfolge
Mittels der Ordinalskala kann eine klare Rangfolge dargestellt werden, zum Beispiel Einfamilienhaus > Doppelhaushälfte > Wohnung. Über die Abstände der Ausprägungen lässt sich jedoch keine Aussage treffen, denn eine Wohnung ist nicht halb so viel wie eine Doppelhaushälfte.
Die Ordinalskala eignet sich zum Beispiel für
- Hochschulrankings
- Rangfolge von Sportlern
- Reihenfolge der drei bevorzugten Restaurants
Einschätzungsskalen
Auch sämtliche Einschätzungsskalen (z. B. von 0 für „trifft nicht zu“ bis 4 „trifft zu“) lassen sich der Ordinalskala zuordnen. In der Praxis werden sie häufig als intervallskaliert betrachet, und zwar im Rahmen einer „Messung per fiat“, also Messung durch Vertrauen. Viele statistische Methoden wären andernfalls kaum bis gar nicht anwendbar.
Intervallskala
Die Intervallskala bietet ergänzend zur Rangfolge der Merkmalsausprägungen Informationen zu den Abständen zwischen den Ausprägungen. Gleich große Unterschiede (als Äquidistanz bezeichnet) werden mittels gleich großer Intervalle dargestellt.
Der Abstand von einem Objekt mit dem Zahlenwert 1 zu einem Objekt mit dem Zahlenwert 2 ist ebenso groß wie der Abstand von einem Objekt mit dem Zahlenwert 4 zu einem Objekt mit dem Zahlenwert 5. Der Nullpunkt sowie die Einheiten auf der Skala können willkürlich und dem jeweiligen Zweck entsprechend gewählt werden.
Die Relationen und Operationen lauten = und ≠, < und > sowie Ø. Operationen bedeuten in diesem Zusammenhang, dass mit den Differenzen gerechnet werden kann.
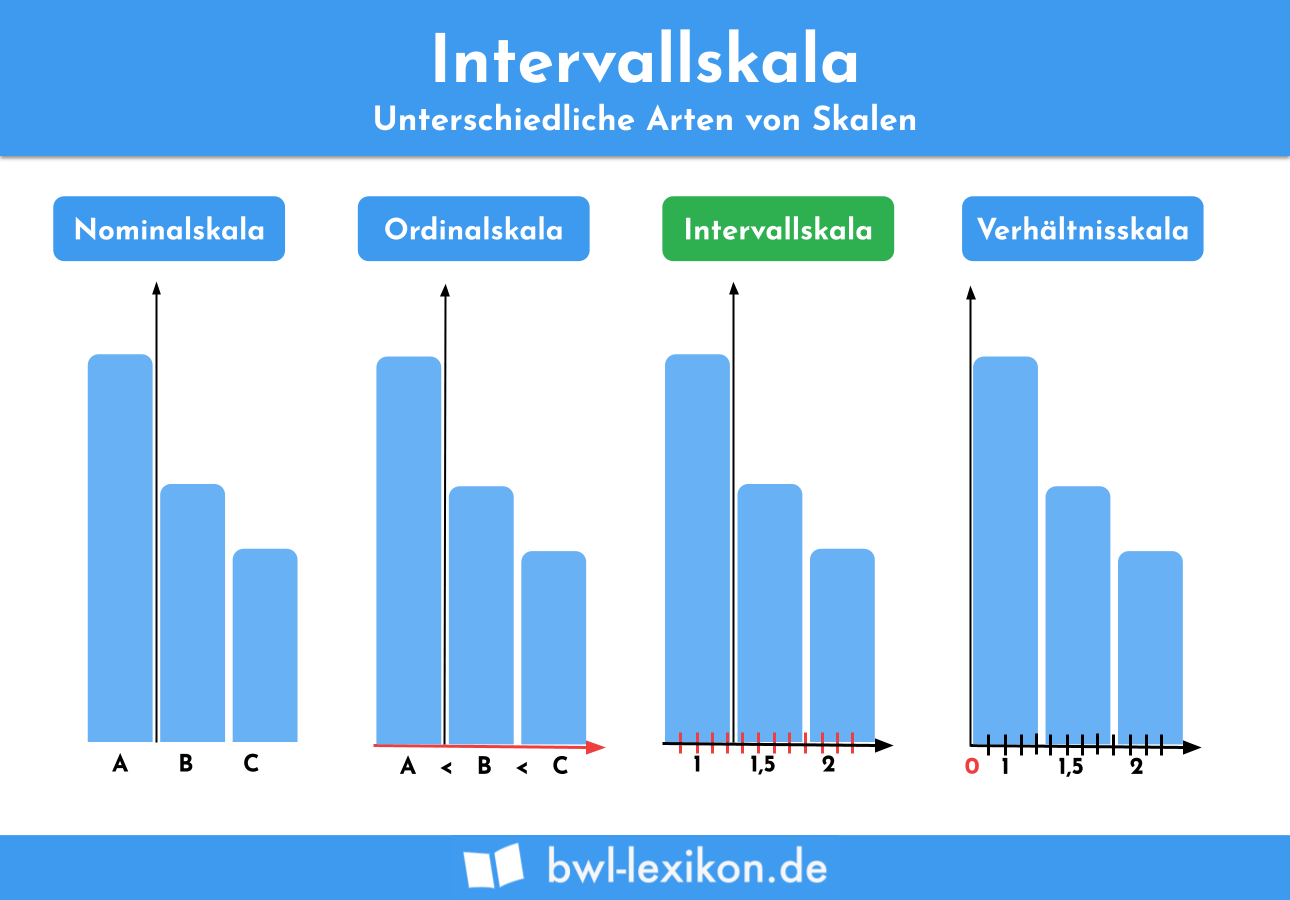
Klassische Beispiele für die Verwendung von Intervallskalen:
- Entfernungen oder Größen in Metern, Zentimetern, Millimetern usw.
- Temperaturen in Celsius, Kelvin, Fahrenheit
- Zeitleisten
- Gewichte in Gramm, Kilogramm etc.
Verhältnisskala
Bei der Verhältnisskala handelt es sich ebenfalls um eine Intervallskala, allerdings besitzt diese einen absoluten Nullpunkt, also einen Anfangspunkt. Der Nullpunkt drückt das Nicht-Vorhandensein eines Merkmals aus, das beim Großteil der messbaren Größen vorkommt wie zum Beispiel Größe, Gewicht und Alter.
Die Relationen und Operationen lauten = und ≠, < und >, + und -, x und :.
Es dürfen Daten zusätzlich multipliziert und dividiert sowie Verhältnisse gebildet werden.
Aussagekraft
Während auf einer Verhältnisskala die Aussage „6 ist doppelt so viel wie 3“ inhaltlich korrekt ist, ist dies auf einer Intervallskala nicht der Fall. 20 Grad Celsius sind nicht doppelt so warm wie 10 Grad Celsius, auch wenn unsere menschliche Wahrnehmung davon ausgehen mag. Umgekehrt sind 100 Grad auf einer Kelvin-Skala tatsächlich doppelt so warm wie 50 Grad, denn auf einer Kelvin-Skala liegt ein natürlicher Nullpunkt (0 Kelvin) vor.
Klassische Beispiele für die Verwendung von Verhältnisskalen:
- Temperatur in Kelvin
- Gewicht in Milligramm, Gramm, Kilogramm etc.
- Größen oder Entfernungen in Kilometern, Metern, Zentimetern, Millimetern etc.
- Einkommen in Euro, Dollar etc.
- Zeiten in Stunden, Minuten, Sekunden etc.
Skalen bewusst wählen
Die Statistik verlangt zulässige Tests, Berechnungen und Darstellungen. Es ist daher wichtig, wie die Merkmale skaliert sind: nominal, ordinal oder wenigstens intervallskaliert. Die Unterscheidung zwischen Intervall- und Verhältnisskala sind für die Statistik allerdings tatsächlich ohne Bedeutung und spielen für die Anwendung kaum eine Rolle. Erst wenn Verhältnisse gebildet werden sollen, sind die Unterschiede zwischen den beiden Skalen relevant. Aus diesem Grund nennen und nutzen viele Fachbücher und sämtliche Statistikprogramme die drei Skalenniveaus Nominal, Ordinal und Intervall.
Übungsfragen
#1. Welche Aussage über quantitative Variablen ist falsch?
#2. Diskrete Variablen sind innerhalb eines beliebigen Intervalls endlich und lassen sich exakt abzählen. Richtig oder falsch?
#3. Bei der Anzahl der Filialen einer Modekette oder dem Gewicht von Welpen eines Wurfs handelt es sich um
#4. Welches Skalenniveau wurde NICHT von Stevens entwickelt?
#5. Die Verhältnisskala eignet sich unter anderem für die Darstellung von Temperaturen in Grad Celsius. Richtig oder falsch?
#6. In der praktischen Statistik ist die Unterscheidung zwischen einer Intervallskala und einer Verhältnisskala von hoher Bedeutung; sie dürfen keinesfalls zusammengefasst werden. Richtig oder falsch?
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
