▷ Kennzahlen der Statistik » Definition, Erklärung & Beispiele + Übungsfragen

In dieser Lektion erhältst du eine Einführung in die Kennwerte der deskriptiven Statistik. Du erfährst detailliert, was es mit dem Maß der zentralen Tendenz, den Streuungsmaßen und der Normalverteilung auf sich hat und findest am Schluss der Lektion einige Übungsfragen zur Vertiefung deines Wissens.

Inhalt dieser Lektion

Nutzen der Kennwerte in der deskriptiven Statistik

Die deskriptive Statistik hat die Aufgabe und das Ziel, in den Daten bestimmte Muster – sofern vorhanden – sichtbar zu machen. Die Daten sollen in eine übersichtliche Form gebracht werden, um sie für Betrachter verständlich und begreiflich zu machen. Im Rahmen der deskriptiven Statistik werden die Daten entsprechend organisiert, zusammengefasst und dargestellt.

Im Grundsatz gibt es dafür zwei Möglichkeiten:

Zusammenfassung der Daten anhand von Kennwerten
grafische oder tabellarische Darstellung der Daten

Umfangreiche Datenmengen und komplexe Zusammenhänge lassen sich auf den ersten Blick kaum durchschauen oder mit Worten kaum so beschreiben, dass die Informationen, die sie liefern können, greifbar werden.

Beispiel

Es soll ermittelt werden, wie alt die Studierenden eines bestimmten Studiengangs im Wintersemester 2022/2023 sind. Zwar liegen Listen (= Daten) vor, in denen das jeweilige Alter (= Merkmalsausprägung) der Studierenden (= Merkmalsträger) angegeben ist. Doch eine schnelle, kurze und präzise Information kann diese Liste auf die konkrete Frage nicht geben.
Kennwerte erlauben dagegen eine schnelle Auswertung und entsprechende Aussagen.

So ist zum Beispiel der jüngste Studierende 19, der älteste 26 Jahre alt (= Spannweite).

Oder es wird das Durchschnittsalter von beispielsweise 23,5 Jahren errechnet (= Mittelwert).

Aussagekraft der Kennwerte

Kennwerte setzen voraus, dass die Verteilung einer Variablen in ausschließlich einem Wert wiedergegeben wird, beispielsweise dem Durchschnittsalter. In vielen Fällen gehen dabei wertvolle Informationen verloren. Es ist wichtig zu wissen, für welche Fragestellung welche Kennwerte geeignet sind und wie diese berechnet werden.

Statistische Kennwerte

Statistische Kennwerte werden häufig schlicht als Statistik oder auch als Maßzahlen bezeichnet. Sie sollen Auskünfte über die Eigenschaften von Verteilungen geben, und zwar in einem aggregierten (zusammengefassten) Format. Viele einzelne Werte werden in deutlich weniger Werte verdichtet, um über die Art und Weise einer Verteilung Auskunft zu geben. Häufig bilden statistische Kennwerte die Basis für nachfolgende statistische Auswertungen.

Mittels statistischer Kennwerte lässt sich die Verteilung einer Variablen beschreiben, und zwar hinsichtlich ihrer zentralen Tendenz und ihrer Streuung.

Das Maß der zentralen Tendenz wird auch als Lagemaß oder Lokationsmaß bezeichnet. Es fasst die Messwerte einer Verteilung zusammen und präsentiert den Schwerpunkt der Verteilung.
Das Streuungsmaß wird auch als Variabilitätsmaß oder Dispersionsmaß bezeichnet. Es informiert darüber, wie unterschiedlich ein Merkmal verteilt ist und um den Schwerpunkt streut.

Beispiel: Statistiche Kennwerte

Monat	verkaufte Pkw
Januar	15
Februar	10
März	16
April	12
Mai	10
Juni	14
Juli	8
August	11
September	12
Oktober	9
November	10
Dezember	7

Daten > Statistische Kennwerte

Mittelwert (Maß der zentralen Tendenz): Ø = 11,17 Pkw pro Monat
Spannweite (Streuungsmaß): 11 Pkw pro Monat

Maß der zentralen Tendenz

Angenommen, es sollen Umfrageergebnisse mitgeteilt werden, zum Beispiel zu den Themen:

Wie viele Menschen in Deutschland fahren einen Familienvan?
Wie beliebt ist unser Bundeskanzler?
Sind Kinder, die in Deutschland leben, übergewichtig?

Um sämtliche Messwerte einer Verteilung zusammenfassend zu repräsentieren, wird ein Kennwert benötigt. Lagemaße geben Auskunft darüber, wo sich das Zentrum oder der Schwerpunkt einer Verteilung befindet. Dazu wird die zentrale Tendenz einer Verteilung anhand von Einheiten auf einer passenden Skala angegeben.

Dass nur ein Wert die gesamte Verteilung möglichst gut beschreiben soll, stellt einen recht hohen Anspruch dar. Es reicht demnach nicht aus, nur die ermittelten Kennwerte zu untersuchen. Die gesamte Verteilung ist bei der Betrachtung zu berücksichtigen; und die Lagemaße müssen gegebenenfalls um Streuungsmaße ergänzt werden.

Es gibt unterschiedliche Maße der zentralen Tendenz; gebräuchlich sind vor allem

Modus
Median
Mittelwert (arithmetisches Mittel)

Modus

In der Verteilung einer diskreten Variablen kommt der Modus (auch als Modalwert bezeichnet) am häufigsten vor. Wird aus der Gesamtheit der Messwerte eine zufällige Stichprobe genommen, kommt dieser Wert am wahrscheinlichsten vor. Gibt es mehr als nur einen Modus, spricht man von einer multimodalen oder einer bimodalen Verteilung. Der Plural von Modus lautet Modi.

Modus

Der Kennwert Modus wird mit Mo. abgekürzt. Die Angabe von Kennwerten erfolgt in lateinischen, üblicherweise kursiv gestellten Buchstaben, hier also konkret Mo.

Beispiel: Modus

Zur Einschulung werden die Körpergrößen von zehn ABC-Schützen gemessen. Folgende Werte werden dabei ermittelt:

111 cm, 115 cm, 113 cm, 111 cm, 116 cm, 114 cm, 110 cm, 117 cm, 111 cm, 115 cm

Der Modus ist Mo = 111 cm, denn dieser Messwert kommt von allen am häufigsten vor.

Merk dir: Beim Modus handelt es sich um den Wert, der am häufigsten auftritt, nicht um den höchsten!

Median

Werden die Messwerte der Größe nach sortiert, wird der Wert, der exakt in der Mitte steht, als Median oder auch als Zentralwert bezeichnet. Die eine Datenhälfte ist kleiner, die andere größer als der Median.

Beispiel: Median

In einer Klassenarbeit erzielen die Schüler folgende Noten: 4, 3, 1, 2, 2, 3, 5, 4, 2, 3, 1

Nach Größe sortiert sieht die Datenreihe folgendermaßen aus: 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 5

Der Median ist die 3.

Zu beachten ist hierbei, dass es nicht in jedem Fall genau eine Person gibt, die exakt in der Mitte steht:

Liegt eine ungerade Anzahl von Werten vor, steht der Median in der Mitte der nach Größe angeordneten Werte.
Liegt eine gerade Anzahl von Werten vor, wird das arithmetische Mittel gebildet, und zwar aus dem kleinsten Wert der oberen Hälfte und dem größten Wert der unteren Hälfte.

Je höher die Anzahl der Werte, desto aufwändiger wird es, den Median zu bestimmen.

Folgende Formel hilft dabei:

$Mitte = \frac{n+1}{2}$

Median

Der Kennwert Median wird mit Md abgekürzt.

Beispiel: Median 1

Es werden die Anzahlen der Follower von elf Influencern auf einer Social Media-Plattform ermittelt.

Dabei ergeben sich folgende Werte:
1105, 1588, 985, 1443, 938, 842, 1116, 4042, 1344, 1837, 1088

Im ersten Schritt werden die Zahlen nach Größe geordnet:
842, 938, 985, 1088, 1105, 1116, 1344, 1443, 1588, 1837, 4042

Mithilfe der Formel wird die Mitte folgendermaßen berechnet:

$\frac{11+1}{2} = 6$

Der sechste Wert beträgt 1116, also ist der Median Md = 1116.

Beispiel: Median 2

Im Nachhinein stellt sich heraus, dass der Wert 4042 aus einem völlig anderen Zusammenhang stammt und aus dieser Liste entfernt werden muss.

Es verbleiben zehn Influencer mit den Werten:
1105, 1588, 985, 1443, 938, 842, 1116, 4042, 1344, 1837, 1088

Die Berechnung sieht nun folgendermaßen aus:
Die Werte werden nach Größe geordnet: 842, 938, 985, 1088, 1105, 1116, 1344, 1443, 1588, 1837

Es liegen nur noch zehn Werte vor. Aufgrund der geraden Anzahl der Werte ist das arithmetische Mittel zu berechnen, und zwar aus dem größten Wert der unteren Hälfte und dem kleinsten Wert der oberen Hälfte.

Der Median befindet sich zwischen dem fünften und dem sechsten Wert, also zwischen 1105 und 1116.

$Md = \frac{1105+1116}{2} = 1110,5$

Da der „Ausreißer“ mit dem Extremwert 4042 entfällt, sinkt der Median entsprechend und erwartungsgemäß; in diesem Beispiel von 1116 auf 1110,5.

Statistische Attribute des Median:

Das Ordinalskalenniveau ist Mindestvoraussetzung.
Vom Median weichen alle übrigen Werte im Durchschnitt am wenigsten ab.
Gegenüber sogenannten Ausreißern ist der Median vergleichsweise wenig anfällig.

Arithmetisches Mittel (Mittelwert)

Der Mittelwert bzw. das arithmetische Mittel ist im geläufigen Sprachgebrauch auch als Durchschnitt bekannt. Er wird gebildet aus der Summe aller Messwerte geteilt durch deren Anzahl.

Gerade wegen der Berechnung aus allen Werten erhalten auch Extremwerte und Ausreißer ein Gewicht, das zur Folge haben kann, dass das arithmetische Mittel die zentrale Tendenz der Werte verzerrt.

Abkürzung

Der Kennwert „arithmetisches Mittel“ wird mit x̄ (x quer) abgekürzt.

Statistische Attribute des Mittelwerts:

Das Intervallskalenniveau ist Mindestvoraussetzung.
Werden die Abweichungen aller Messwerte vom Mittelwert aufsummiert, lautet das Ergebnis Null.
Sämtliche Werte werden bei der Berechnung berücksichtig. Der Mittelwert ist daher anfällig für Ausreißer.

Beispiel: Arithmetisches Mittel 1

Wie lautet der Mittelwert der Anzahl der elf Influencer-Follower aus dem obigen Beispiel?

Die Werte lauten:
1105, 1588, 985, 1443, 938, 842, 1116, 4042, 1344, 1837, 1088

$x̄ = \frac{Summe~der~Follower}{Anzahl~der~Influencer}$

$x̄ = \frac{16328}{11} \approx 1484,36$

Beispiel: Arithmetisches Mittel 2

Der Extremwert von 4042 wird auch hier gestrichen; die Werte lauten nun: 1105, 1588, 985, 1443, 938, 842, 1116, 1344, 1837, 1088

$x̄ = \frac{12286}{10} = 1228,6$

Unterschied zwischen Median und Mittelwert

Im Vergleich zum Median unterscheidet sich der Mittelwert nach Entfernen eines einzelnen Wertes deutlich vom vorherigen Ergebnis, während der Median sich nur geringfügig geändert hat – ein eindrucksvolles Beispiel dafür, wie anfällig der Mittelwert für derartige Extremwerte bzw. Ausreißer ist: Ein einzelner Wert reicht aus, um das Ergebnis signifikant zu beeinflussen.

Streuungsmaße

Zwar können Verteilungen gleiche Maße der zentralen Tendenz, wie beispielsweise den Mittelwert, aufweisen, aber die Streuung der Werte um diese Maße können unterschiedlich breit streuen.
Beispiel: Der Notendurchschnitt (Mittelwert) einer Klassenarbeit beträgt genau 3 für „befriedigend“. Die Gründe dafür können aber völlig unterschiedlich sein:

Note	Anzahl der Schüler Möglichkeit 1	Anzahl der Schüler Möglichkeit 2	Anzahl der Schüler Möglichkeit 3	Anzahl der Schüler Möglichkeit 4
1	15	6	4	0
2	0	6	6	0
3	0	6	10	30
4	0	6	6	0
5	15	6	1	0
Mittelwert	3	3	3	3

Für die Streuung muss es ein Maß geben, das anhand eines einzigen Wertes einen Schluss darauf zulässt, wie sich die Werte um den Mittelwert streuen. Es gibt dafür eine Kennwert-Gruppe, genannt Streuungsmaße, die genau diesen Anspruch erfüllt.

Die Streuungsmaße informieren darüber, in welchem Umfang die Werte um die zentrale Tendenz verteilt sind.

Sie werden auch als Dispersionsmaße bezeichnet und wie folgt unterschieden:

Spannweite bzw. Range
Interquartilsabstand
Varianz
Standardabweichung

Spannweite bzw. Range

Die Spannweite gibt die Differenz zwischen dem größten Wert (Maximum) und dem kleinsten Wert (Minimum) an.

Beispiel: Spannweite

Wir verwenden noch einmal die Anzahl der Influencer-Follower: 1105, 1588, 985, 1443, 938, 842, 1116, 1344, 1837, 1088

Der kleinste Wert (Minimum) beträgt 842, der größte (Maximum) 1837.

$Spannweite = 1837 - 842 = 995$

Ein großer Nachteil bei der Spannweite liegt darin, dass nur die beiden Randwerte berücksichtigt werden. Sie ist also stark abhängig von Extremwerten.

Interquartilsabstand

Der Nachteil der Spannweite lässt sich mittels des Interquartilsabstands aushebeln. Extremwerte werden aus der Analyse ausgeschlossen und es werden zum Beispiel nur die 50 Prozent der Werte in der Mitte der Verteilung berücksichtigt. Dieser Bereich wird als Interquartilsbereich oder als Interquartilsabstand bezeichnet. Aufgrund des eingeschränkten Bereichs wird das Ergebnis nur in geringem Ausmaß durch Ausreißer bzw. Extremwerte beeinflusst.

Die Berechnung ist dem des Median sehr ähnlich. Der erste Schritt besteht darin, die Werte der Größe nach zu sortieren. Anschließend wird die Werteverteilung in vier gleiche Teile (Quartile) eingeteilt. Der Interquartilsabstand ist die Spannweite zwischen dem Anfang des zweiten und dem Ende des dritten Quartils.

Beispiel: Alter der Mitarbeiter eines Unternehmens

Schritt 1:

Alter	20	21	22	23	24	25	26	27	28	229	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45
Anzahl MA	1	1	1	1	1	1	1	1	1	1	1	1			1	1			1							1

Schritt 2:

Alter	20	21	22	23	24	25	26	27	28	229	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45
Anzahl MA	1	1	1	1	1	1	1	1	1	1	1	1			1	1			1							1
	1. Quartil				2. Quartil				3. Quartil				4. Quartil

Note	Anzahl der Schüler Möglichkeit 1	Anzahl der Schüler Möglichkeit 2	Anzahl der Schüler Möglichkeit 3	Anzahl der Schüler Möglichkeit 4
1	15	6	4	0
2	0	6	6	0
3	0	6	10	30
4	0	6	6	0
5	15	6	1	0
Mittelwert	3	3	3	3

Die Formeln zur Ermittlung der beiden Randwerte lauten 0,25 x n bzw. 0,75 x n. Im Beispiel sind 16 Werte vorhanden, damit ist n = 16.

Die Formeln lauten demnach:

$0,25 * 16 = 4$

und

$0,75 * 16 = 12$

Der Interquartilsabstand befindet sich also zwischen dem 4. Wert (= 23) und dem 12. Wert (= 31).
Ist das Ergebnis der Berechnung ungerade, wird aufgerundet.

Beispiel: Die Anzahl der Werte beträgt 10.

$0,25 * 10 = 2,5$

→ aufgerundet 3
und

$0,75 * 10 = 7,5$

→ aufgerundet 8.

Für den Interquartilsabstand wird die Abkürzung IQR (englisch: interquartil range) verwendet.

Statistische Attribute des Interquartilabstands:

Innerhalb des Interquartilabstands befinden sich immer insgesamt 50 Prozent der Daten.
Gegenüber Ausreißern ist der Interquartilsabstand nicht anfällig.

Der Nachteil des Interquartilabstands besteht darin, dass er nicht alle Werte der Verteilung, sondern lediglich zwei Randwerte berücksichtigt.

Varianz

Bei der Varianz handelt es sich – dem arithmetischen Mittel entsprechend – um einen Kennwert, der sämtliche Werte einer Verteilung berücksichtigt; in diesem Fall sämtliche Abweichungen vom Mittelwert. Dazu werden die Abstände der Werte zum Mittelwert aufsummiert. Je größer die Streuung ist, desto größer wird der Kennwert.

Allerdings beinhaltet dieses Vorgehen ein Problem: Abweichungen im positiven und im negativen Bereich heben sich gegenseitig zum Wert Null auf. Daher werden die Abweichungen quadriert und diese aufsummiert (= Quadratsumme, englisch sum of squares).

Abkürzung Quadratsumme

Für die Quadratsumme wird die Abkürzung QS verwendet.

An diesem Punkt taucht ein weiteres Problem auf. Je mehr Werte vorliegen, desto größer wird die Varianz, denn die Größe der Quadratsumme ist abhängig von der Anzahl der Messwerte.
Benötigt wird jedoch ein Maß, das nicht von der Größe der Stichprobe abhängt. Daher wird das Ergebnis in Relation zur Anzahl der Merkmalsträger der Stichprobe gesetzt und durch die Anzahl der Messwerte geteilt.

$\begin{displaymath} s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x}) \end{displaymath}$

Abkürzung Varianz

Für die Varianz wird die Abkürzung s² verwendet.

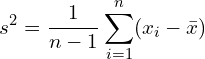
Die mathematischen Attribute der Varianz:

Größere Abweichungen erhalten ein höheres Gewicht bei der Berechnung.
Sämtliche Abweichungen sind positiv.

Die Vorteile der Varianz:

Es werden alle Werte der Verteilung berücksichtigt.
Die Größe der Kennwerte ist ein Maß für die Stärke der Streuung um den Mittelwert.

In der Statistik genießt die Varianz daher einen hohen Stellenwert. Aber sie hat auch einen Nachteil: Der sich aus der Berechnung ergebende Wert lässt sich aufgrund des Quadrierens nur schwer deuten. Für eine leichtere Interpretation muss das Quadrieren wieder aufgehoben werden.

Die Lösung ist denkbar einfach: Aus der Varianz wird die Wurzel gezogen.

Bei diesem neuen (quadrierten) Kennwert handelt es sich übrigens um die Standardabweichung.

Standardabweichung

Bei der Standardabweichung handelt es sich schlicht um die positive Wurzel der Varianz. Die Formel sieht folgendermaßen aus:

$\begin{displaymath} s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2} \end{displaymath}$

Abkürzung Standardabweichung

Die Standardabweichung wird mit s oder sd (engl. standard deviation) abgekürzt.

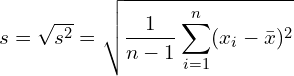
Die Standardabweichung ist ein Maß, das die durchschnittlichen Abweichungen vom Mittelwert aufzeigt. Mittels dieser Kenngröße lässt sich erkennen, wie zutreffend ein Mittelwert die Werteverteilung repräsentiert.

Je größer die Standardabweichung relativ zum Mittelwert ist, desto größer ist die Abweichung der einzelnen Werte vom Mittelwert.

Der Kennwert „Standardabweichung“ erfreut sich in der Statistik hoher Beliebtheit. Ist die zugrundeliegende Variable normalverteilt, lässt er noch mehr Rückschlüsse zu.

Normalverteilung

Im Jahr 1844 machte der belgische Astronom und Statistiker Adolphe Quetelet eine überraschende Entdeckung, und zwar im Zuge einer Untersuchung mehrerer tausend Soldaten. So wurde unter anderem deren Brustumfang gemessen; und es zeigte sich, dass die Messwerte in einem Diagramm ein symmetrisches, glockenförmiges Bild ergeben.

Carl Friedrich Gauß hatte diese Verteilung bereits im 1809 theoretisch hergeleitet, und in der Natur ist die sogenannte Normalverteilung annähernd überall zu finden.

Bei der Normalverteilung ist die Verteilung unimodal (= es gibt nur einen einzigen Höchstwert) und symmetrisch (= rechts und links sind gleich); der Verlauf ist glockenförmig. Es gibt deutlich mehr als nur eine Normalverteilung, aber jede kann mithilfe von zwei Werten eindeutig definiert werden:

Sind der Mittelwert und die Standardabweichung bekannt, ist die Werteverteilung ebenfalls bekannt. Warum?

Die Standardabweichung bildet den Abstand des Mittelwerts zum Wendepunkt ab. Zwischen den Wendepunkten links und rechts vom Mittelwert liegen etwa zwei Drittel (ca. 68 Prozent) sämtlicher Messwerte. Ist die Standardabweichung bekannt, lassen sich mühelos Rückschlüsse auf die Werteverteilung ziehen.

Beispiel: Normalverteilung

Wir wissen, dass normalgewichtige Golden Retriever-Rüden im Schnitt 32 Kilogramm wiegen. Die Standardabweichung beträgt zwei Kilogramm. Daraus lässt sich ableiten, dass zwei Drittel der normalgewichtigen Golden Retriever-Rüden zwischen 30 und 34 Kilogramm auf die Waage bringen.

Kennzahlen der Statistik

Nutzen der Kennwerte in der deskriptiven Statistik