Lineare Regression

Bei der Linearen Regression handelt es sich um eine spezielle Form der Regressionsanalyse, bei der nur solche Zusammenhänge betrachtet werden, bei denen die abhängigen Variablen eine lineare Kombination der Regressionskoeffizienten aufweisen.

Wir zeigen dir in diesem Abschnitt, was man unter einer linearen Regression versteht und welche Bedeutung sie hat. Anhand der im Anschluss folgenden Übungsaufgaben kannst du dein Wissen zur linearen Regression testen.

Synonym: lineare Einfachregression

Welche Bedeutung hat die lineare Regression?

Als statistisches Verfahren ist die lineare Regression ein sehr vielseitig einsetzbares Verfahren. Sie kann beispielsweise zur Untersuchung von bestimmten Zusammenhängen herangezogen werden, genauso aber auch zur Erstellung von Prognosen und Vorhersagen für zukünftige Entwicklungen.

Beispiele dafür sind:

• Die Untersuchung von Einsatz der Werbemittel und Steigerung des Umsatzes zur Einschätzung der Rentabilität
• Vorhersagen über zukünftige Trendentwicklungen
• Prognosen über Besucherzahlen in einem Geschäft oder bei einer Veranstaltung

Was versteht man unter der linearen Regression?

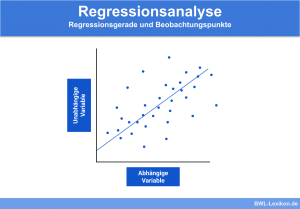
Die lineare Regression ist ein Verfahren aus der Statistik, welches den Zusammenhang zweier Variablen, einer unabhängigen und einer abhängigen, darstellt. Dabei werden die aufgenommen Datenpunkte zu den einzelnen Variablen in ein Diagramm eingetragen und zwischen ihnen eine Regressionsgerade gelegt.

Die Funktion dieser Regressionsgeraden sieht folgendermaßen aus:

β₀ und β₁ stellen dabei die Regressionskoeffizienten dar. β₀ ist dabei die Regressionskonstante, die angibt, welchen Wert die abhängige Variable y in dem Fall annimmt, in dem die unabhängige Variable x = Null ist.

Voraussetzung für eine inhaltliche Interpretation der Regressionskonstante ist, dass die unabhängige Variable überhaupt gleich Null sein kann.

β₁ als Regressionskoeffizient beschreibt die Steigung der Regressionsgeraden, was bedeutet, dass sie angibt, wie stark die Änderung der abhängigen Variable aufgrund einer Änderung der unabhängigen Variablen ist. Je höher β₁ also ist, desto größer ist der Einfluss der unabhängigen auf die abhängige Variable.

Voraussetzungen für die lineare Regression

Zur korrekten Interpretation der linearen Regression müssen die folgenden Voraussetzungen gegeben sein:

• Es besteht ein zumindest grob linearer Zusammenhang zwischen den beiden betrachteten Variablen.
• Die abhängige Variable sollte nach Möglichkeit metrisch sein.
• Die unabhängige Variable kann metrisch, aber auch dichotom-kategorial sein.
• Zwischen den Residuen besteht keine Korrelation.
• Die Residuen sind annähernd normalverteilt.
• Die Residuen sind über den gesamten Wertebereich der abhängigen Variablen gestreut.

Beispiel zur linearen Regression

Die „Eisjungen AG“ möchte eine neue Eissorte auf den Markt bringen. Um zu untersuchen, zu welchem Zeitpunkt (unabhängige Variable) am meisten Eis verkauft (abhängige Variable) wird, werden die in der Vergangenheit erhobenen Werte von Temperatur und verkaufter Menge untersucht.

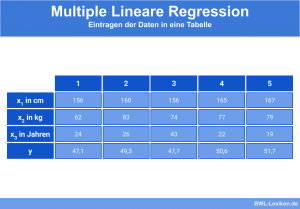
Folgende Daten wurden erhoben:

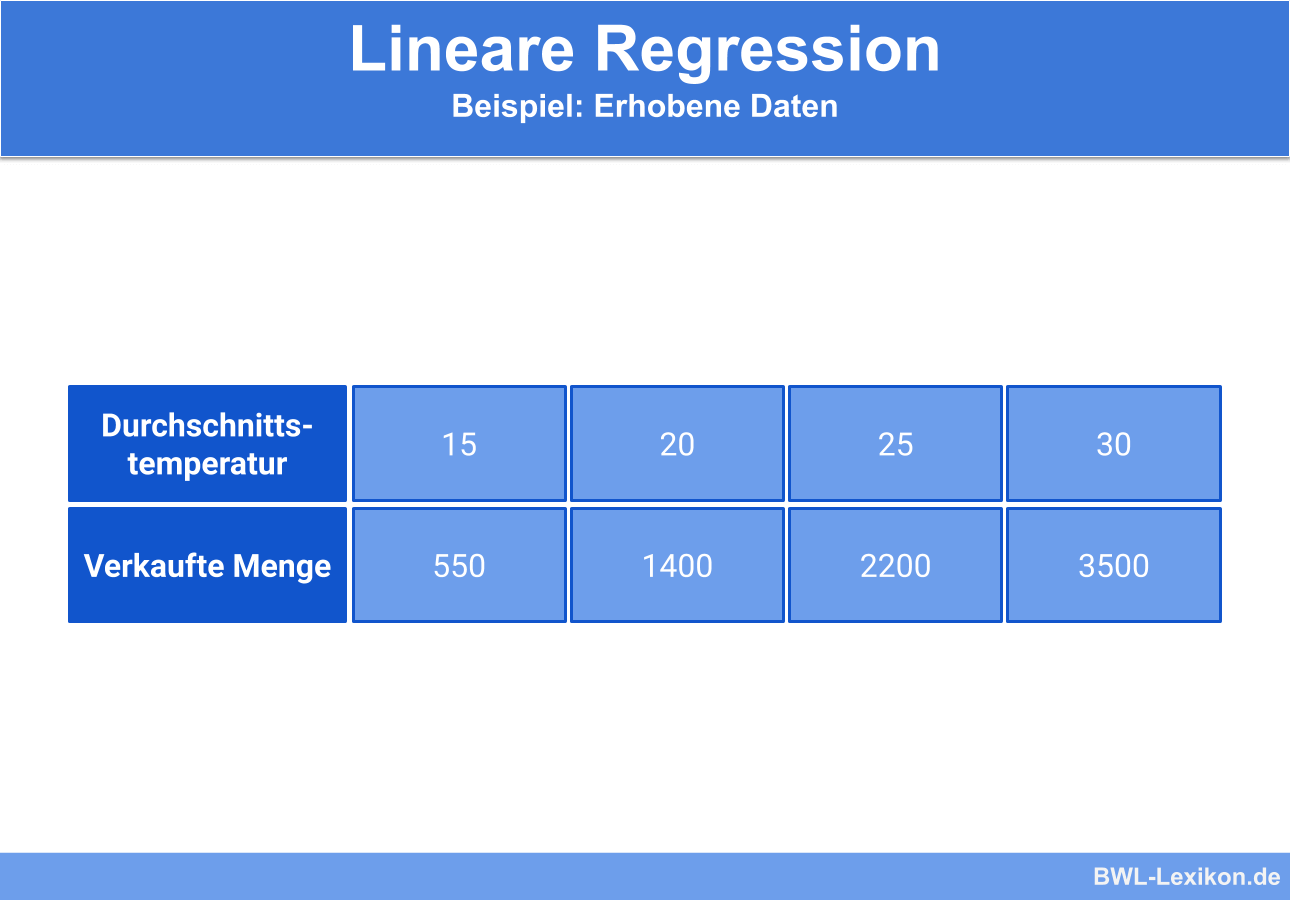
Die ermittelten Werte werden nun in ein Diagramm eingetragen:

Anhand des Diagramms kann man erkennen, dass ein linearer Zusammenhang zwischen den beiden Variablen besteht.

Es kann also eine Regressionsgerade durch die Punkte gelegt werden:

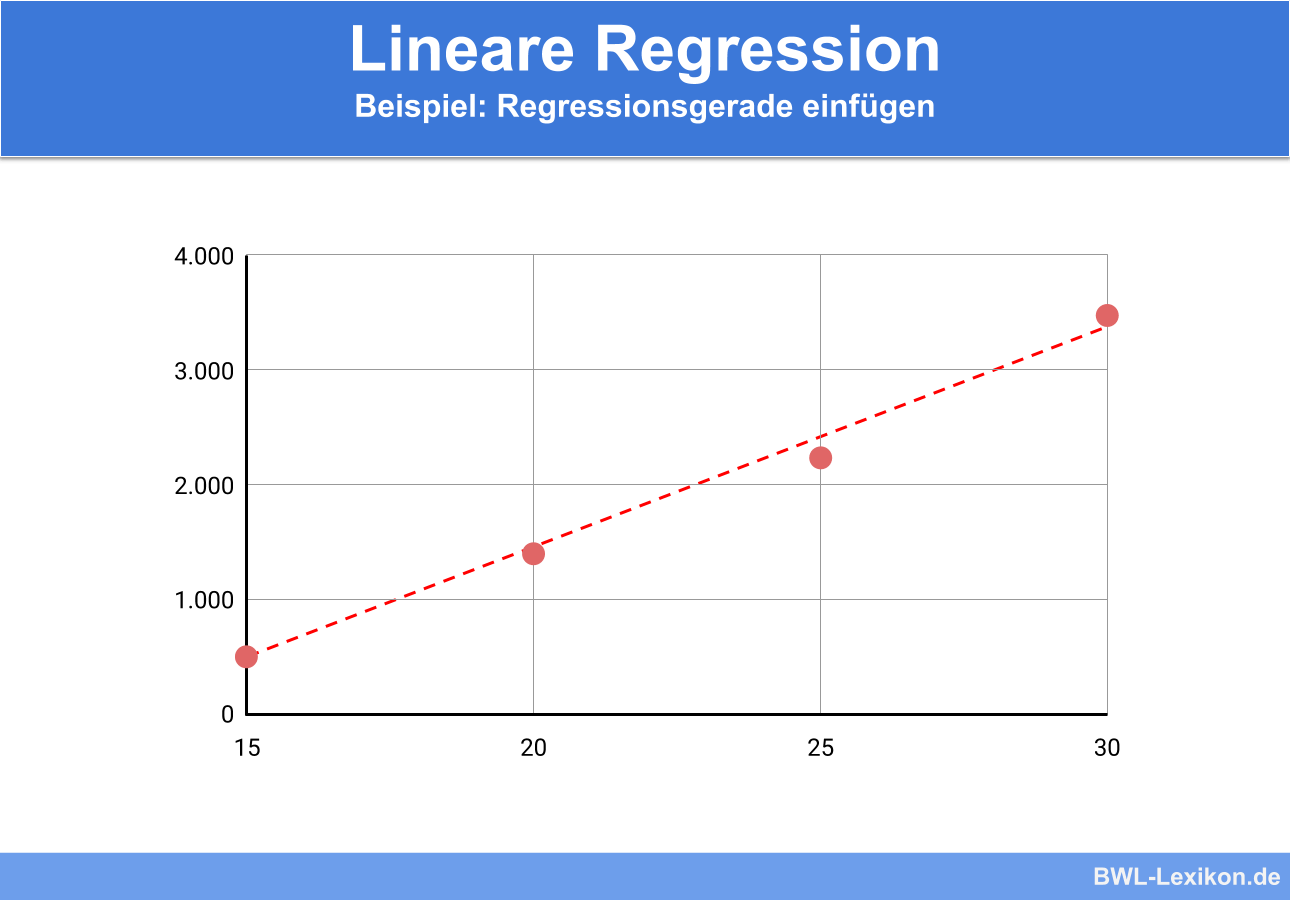
Übungsfragen