Der Eulerkreis ist ein mathematisches Konstrukt in der Graphentheorie. Kennzeichnend ist, dass der Eulerkreis ein Zyklus ist, bei dem alle Kanten eines Graphen genau einmal vorhanden sind. Der Eulerweg geht auf seinen Entdecker, Leonhard Euler, zurück.
In diesem Text erfährst du, was sich hinter dem Eulerweg verbirgt. Wir erklären dir, was der Eulerkreis ist und welcher Zyklus sich dahinter verbirgt. Nachdem du weißt, in welchem Zusammenhang der Eulerweg mit dem Königsberger Brückenproblem steht, grenzen wir abschließend den Eulerkreis vom Hamiltonkreis ab. Damit du deinen Wissensstand zum Eulerkreis erweiterst, kannst du nach diesem Beitrag einige Übungsfragen beantworten.
Synonym: Eulerweg
Was solltest du über den Eulerkreis wissen?
Die mathematische Graphentheorie kennt die beiden folgenden Konstrukte:
- Eulerkreis
- Hamiltonkreis
Der Eulerkreis wurde von dem Schweizer Mathematiker Leonhard Euler (1707 bis 1783) entdeckt. Er beschreibt einen Zyklus, der sich dadurch kennzeichnet, dass alle Kanten eines Graphen genau einmal vorhanden sind.
Ein Zyklus entsteht in der Mathematik dadurch, dass der Anfangsknoten dem Endknoten eines Pfades entspricht. Der Eulerkreis ist eine bestimmte Form des Zyklus. Mit dessen Hilfe ist Leonhard Euler das Königsberger Brückenproblem angegangen. Der Eulerkreis grenzt sich von anderen mathematischen Konstrukten – wie z. B. dem Hamiltonkreis – ab.
Welcher Zyklus verbirgt sich hinter dem Eulerweg?
Der Zyklus im Eulerweg setzt voraus, dass jede Kante nur einmal genutzt werden kann. Azyklische Graphen sind bei der Anwendung des Eulerkreises nicht vorgesehen.
Ein Eulerkreis unterscheidet sich insofern vom Eulerweg, als dass dort kein Knoten einen ungeraden Grad hat.
Euler widmete sich dem Problem, ob es um die Stadt Königsberg einen Rundweg gibt, bei dem man alle sieben Brücken genau einmal überqueren muss und anschließend wieder am Ausgangspunkt angelangt. Mithilfe seiner in die Praxis umgesetzte Theorie bewies Leonhard Euler, dass es keinen solchen Rundweg um Königsberg gibt.
Zu berücksichtigen ist allerdings, dass es sich bei dem Königsberger Brückenproblem um kein rein geometrisches Problem handelt. Denn es kommt hierbei nur darauf an, dass die Brücken über den Rundweg miteinander verbunden werden. Die genaue Lage der Brücken war für Euler aber unerheblich.
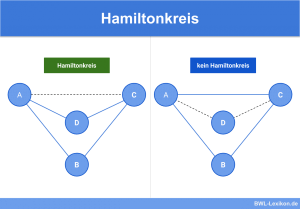
Wodurch grenzt sich der Eulerkreis vom Hamiltonkreis ab?
Der Hamiltonkreis ist ein weiteres Konstrukt in der mathematischen Graphentheorie. Kennzeichnend ist, dass die Kanten eines Graphen im Hamiltonkreis keinen hohen Stellenwert einnehmen. Hier durchläuft jeder Knoten einen Graphen. Anfangsknoten und Endknoten müssen beim Hamiltonkreis nicht identisch sein. Dies ist bei Anwendung des Eulerkreises eine zwingende Voraussetzung.
Übungsfragen
#1. Wodurch zeichnet sich der Eulerweg aus?
#2. Wovon grenzt sich der Eulerkreis ab?
#3. Welches Problem hat Leonhard Euler 1736 mithilfe des Eulerkreises gelöst?
#4. Welche Aussage zum Eulerkreis ist nicht korrekt?
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen