▷ Lineare Optimierung » Definition, Erklärung & Beispiele + Übungsfragen

Die lineare Optimierung ist eines der hauptsächlich genutzten Verfahren im Operations Research und befasst sich mit der Optimierung von linearen Zielfunktionen, unter der Einschränkung von linearen Gleichungen und Ungleichungen.

Wir zeigen dir in diesem Kapitel, warum die lineare Optimierung wichtig ist, zu welchem Zweck Sie genutzt werden kann und wie Sie angewendet wird. Daneben stellen wir dir am Ende Übungsaufgaben zur Verfügung, mit denen du dein Wissen zur Linearen Optimierung überprüfen kannst.

Synonyme: lineare Programmierung | lineare Planungsrechnung

Inhalt dieser Lektion

Warum ist Lineare Optimierung wichtig?

Die lineare Optimierung wird überall dort angewendet, wo die Minimierung bzw. Maximierung einer Zielfunktion unter bestimmten Restriktionen erarbeitet werden soll.

In der betrieblichen Praxis ist dies besonders häufig in folgenden Bereichen der Fall:

Optimierung der Produktionsplanung hinsichtlich der optimalen Kapazitätsauslastung
Optimierung von Futtermischungen für die Landwirtschaft
Optimierung von Verschnittmengen in der Produktion
Optimierung von Transport- und Tourenplänen
Ermittlung optimaler Losgrößen in der Produktion und Bestellmengen im Einkauf
Ermittlung optimaler Investitionsprogramme
Erstellung optimaler Einsatzpläne der Mitarbeiter
Ermittlung der optimalen Absatzmenge
Optimierung von Marketingmaßnahmen

In der Praxis werden hierzu spezielle Software-Programme genutzt, da diese eine wesentliche Zeitersparnis bei der Problemlösung mit sich bringen.

Was versteht man unter linearer Optimierung?

Bei der linearen Optimierung handelt es sich um ein mathematisches Verfahren, welches im Zuge des Operations Research eingesetzt wird. Es dient der Minimierung bzw. Maximierung einer linearen Funktion, welche bestimmten Restriktionen unterliegt.

Die Bestandteile der linearen Optimierung sind:

Die Zielfunktion, beispielsweise die Maximierung des Erlöses oder Minimierung der Kosten
Die Restriktionen, beispielsweise die maximalen Produktionskapazitäten
Die Bedingung der Nichtnegativität, d.h. alle Variablen innerhalb der Linearen Optimierung müssen gleich oder größer als Null sein

Ziel der linearen Optimierung ist die Lösung von Problemen durch die Ermittlung einer oder mehrerer optimaler Lösungen. Existiert keine optimale Lösung, so kann die lineare Optimierung auch zu diesem Ergebnis führen.

Die lineare Optimierung kann sowohl mathematisch als auch graphisch gelöst werden. Lässt sich das Problem nicht mit der linearen Optimierung lösen, so können andere Methoden angewendet werden, beispielsweise mit Hilfe einer Simulation oder der Netzplantechnik.

Anwendung der linearen Optimierung

Die Schokobox AG ist im Süßwarengeschäft tätig. Sie produziert sowohl Pralinen als auch Schokoladentafeln. Für den kommenden Monat sollen die optimalen Produktionsmengen für Pralinenschachteln und Schokoladentafeln berechnet werden, um den Deckungsbeitrag zu maximieren.

Dabei gilt:

$x_1 = Pralinenschachteln$

$x_2 = Schokoladentafeln$

Die Pralinenschachteln erzielen pro Stück einen Gewinn von 4 €, Schokoladentafeln einen gewinn von 2 €.

Zur Anwendung der Linearen Optimierung wird zuerst die Zielfunktion aufgestellt:

$ZF: max~4 x_1 + 2 x_2$

Als nächstes müssen die Restriktionen, denen die Zielfunktion unterliegt festgestellt werden. Der Vertrieb hat in seiner Absatzplanung ermittelt, dass im nächsten Monat maximal 200 Pralinenschachteln und 400 Schokoladentafeln verkauft werden können.

Die ersten beiden Nebenbedingungen lauten also:

$x1 \leq 200$

$x2 \leq 400$

Die zweite Restriktion ist durch die Produktionskapazität gegeben. Auf der Produktionslinie kann im gesamten Monat maximal 150 Stunden produziert werden. Die Produktion einer Schokoladentafel dauert 2 Stunden, die einer Pralinenschachtel 3 Stunden.

Die dritte Nebenbedingung lautet also:

$2x_1 + 3x_2 \leq 150$

Außerdem stehen 200 Arbeitsstunden des Personals zur Verfügung, wobei die Produktion einer Pralinenschachtel 6 Arbeitsstunden erfordert. Für eine Schokoladentafel sind hingegen nur 2 Arbeitsstunden notwendig.

Daraus ergibt sich eine weitere restriktive Nebenbedingung:

$6x_1 + 2x_2 = 200$

Die immer geltende Nichtnegativitätsbedingung stellt die letzten beiden Restriktionen dar:

$x_1 \geq 0$

$x_2 \geq 0$

Ermittlung der Produktionsmenge mit der graphischen Methode

Um die optimale Produktionsmenge beider Produkte zu ermitteln, kann zum einen die graphische Methode angewendet werden.

Hierzu werden die Nebenbedingungen und die zunächst nach x2 aufgelöst und anschließend in ein Koordinatensystem eingetragen:

$x1 \leq 200$
$x2 \leq 400$
$2x_1+3x_2 \leq 150 \longrightarrow x_2 \leq 75 - \frac{3}{2}x_1$
$6x_1+2x_2 \leq 200 \longrightarrow x_2 \leq 100 - 3x_1$
$x_1 \geq 0$
$x_2 \geq 0$

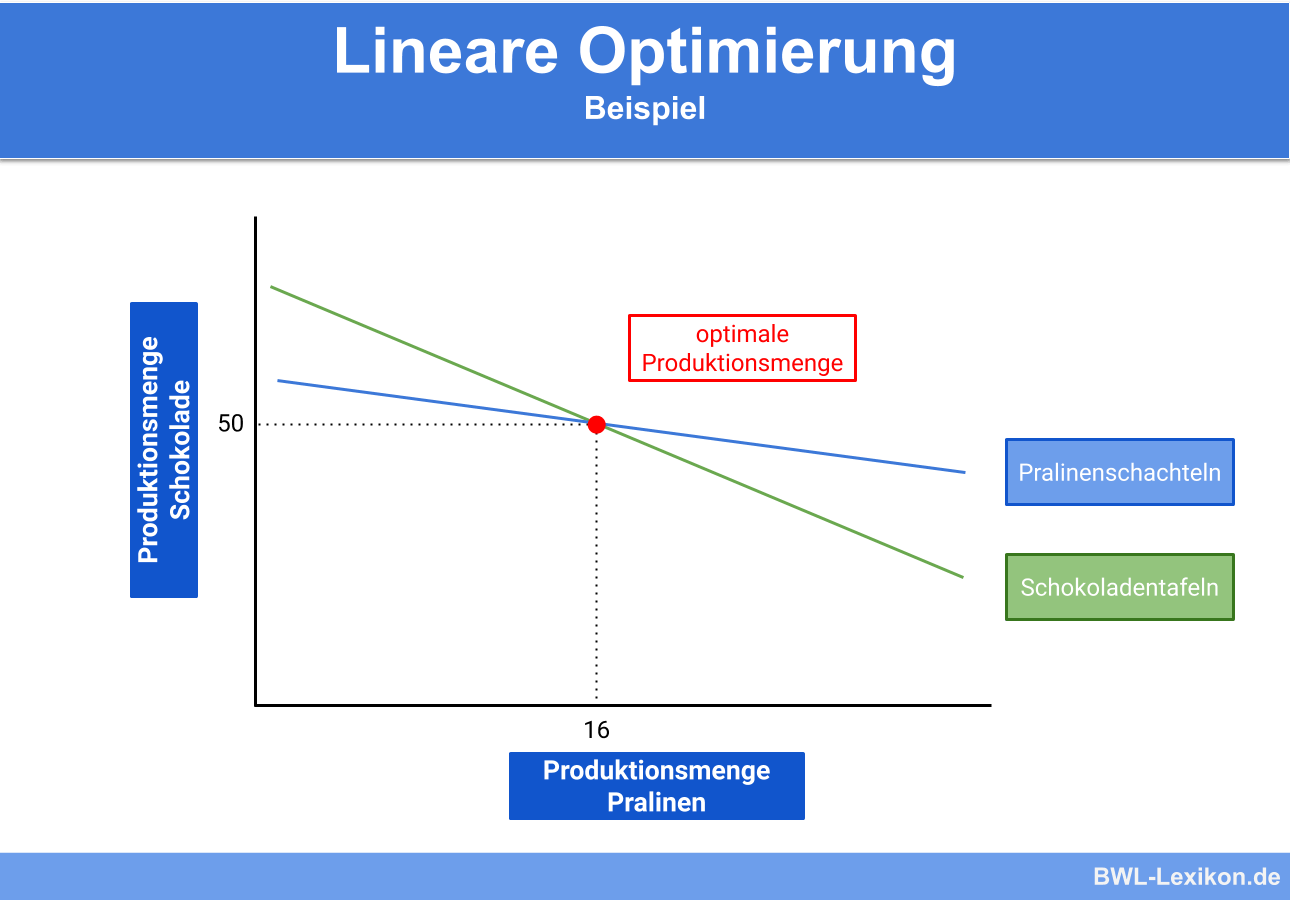
Lineare Optimierung - Beispiel — Lineare Optimierung – Beispiel

Am Schnittpunkt beider Geraden können die optimalen Produktionsmengen abgelesen werden, wobei die x-Achse für die Pralinenschachteln und die y-Achse für die Schokoladentafeln steht.

Nach der graphischen Lösung erhält die Schokobox AG als optimale Produktionsmengen also:

ca. 16 Pralinenschachteln
ca. 50 Schokoladentafeln

Ermittlung der Produktionsmenge mit der rechnerischen Methode

Um ein genaues Ergebnis zu erhalten, wird die rechnerische Methode angewendet.

Hierzu werden die Funktionen der beiden vorher eingezeichneten Geraden gleichgesetzt und zuerst nach x1 aufgelöst:

$75 - \frac{3}{2}*x_1 = 100-3x_1$

$x_1= 16,66$

Dieser Wert wird in eine der beiden Gleichungen eingesetzt, um x2 zu erhalten:

$x_2 = 100-3*16,66$

$x_2 = 50$

Rechnerisch beträgt die optimale Produktionsmenge also 16,66 Pralinenschachteln und 50 Schokoladentafeln.

Vorteile und Nachteile der Linearen Optimierung

Vorteile:

Für verschiedenste Prozesse kann eine oder mehrere optimale Lösungen gefunden werden.
Durch die gefundene optimale Lösung können die Kosten minimiert bzw. der Gewinn des Betriebs maximiert werden.

Nachteile:

Die Durchführung der Linearen Optimierung erfordert in der betrieblichen Praxis den Einsatz spezieller Software-Programme, da eine händische Lösung in den meisten Fällen zu aufwendig ist.