Unter der Regressionsanalyse versteht man eine statistische Analysemethode, mit der man mögliche Zusammenhänge zwischen zwei oder mehr Variablen feststellen kann. Im Ergebnis der Untersuchung entsteht eine Regressionsgerade, anhand derer die Abhängigkeit der Variablen voneinander abgelesen werden kann.
Dieses Kapitel bringt dir näher, welche Bedeutung die Regressionsanalyse hat und was man genau darunter versteht. Anhand der anschließenden Übungsaufgaben kannst du überprüfen, inwieweit dein Wissen zu diesem Thema bereits gefestigt ist.
Welche Bedeutung hat die Regressionsanalyse?
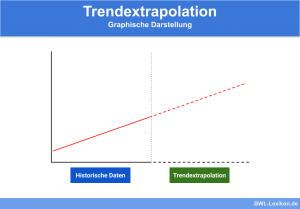
Mit Hilfe der Regressionsanalyse kann die Abhängigkeit mehrerer Variablen untersucht werden. Dies ist vor allem wichtig, wenn statistische Beobachtungen untersucht und erklärt werden sollen, aber auch, um mögliche Vorhersagen über die Zukunft machen zu können. Insbesondere bei der strategischen Unternehmensplanung ist dies ein wichtiger Teil, um die Unternehmensstrategie entsprechend auszurichten.
Was versteht man unter der Regressionsanalyse?
Die Regression beschreibt den Zusammenhang zwischen zwei oder mehr unabhängigen und abhängigen Variablen.
Eine abhängige Variable ist dabei immer abhängig von einer oder mehreren unabhängigen Variablen. Das bedeutet, dass eine Veränderung einer unabhängigen Variable automatisch eine entsprechende Reaktion der abhängigen Variablen auslöst.
Eine unabhängige Variable hingegen ist nicht durch den Einfluss einer anderen Variablen bestimmt. Sie kann selbst bestimmt und verändert werden, um mögliche Veränderungen der von ihr abhängigen Variablen zu beeinflussen.
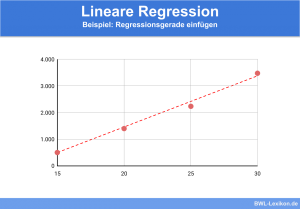
Mit der Regressionsanalyse wird der Zusammenhang zwischen den betrachteten Variablen untersucht. Das Ziel ist es, eine Regressionsfunktion bzw. eine Regressionsgerade zu bestimmen, die den Zusammenhang der Variablen beschreibt.
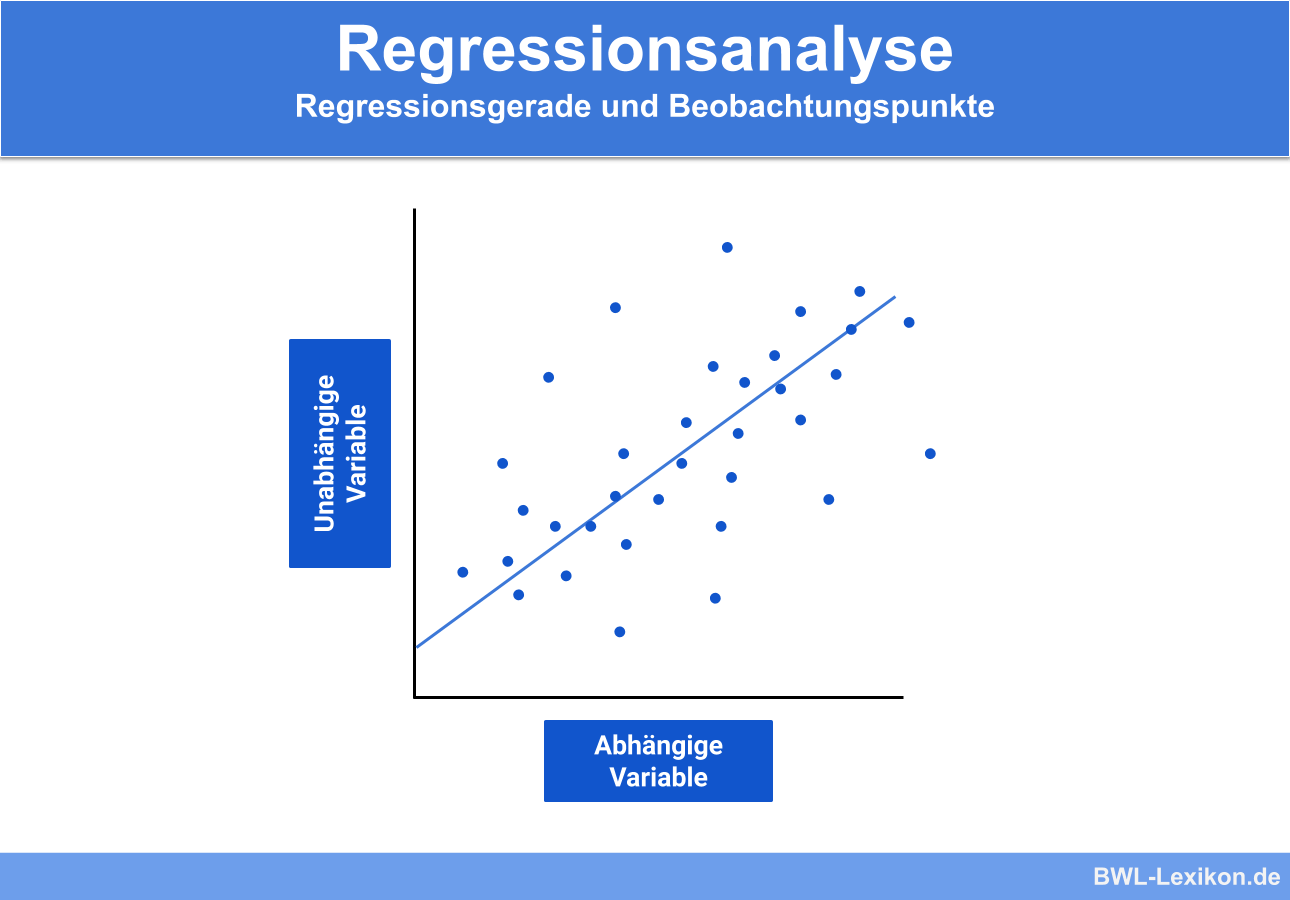
In der Regressionsanalyse unterscheidet man verschiedene Arten, diese sind:
- die Lineare Regression
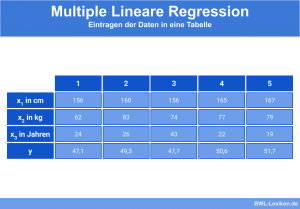
- die Multiple (lineare) Regression
- die Multinominale Regression
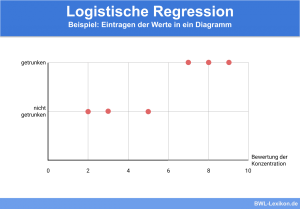
- die Logistische Regression
- die Multivariate Regression
Ist die Regressionsfunktion ermittelt, so gibt dies noch keine Aussage darüber, ob diese signifikant ist, also ob sie auch auf die Gesamtheit der Variablen übertragen werden kann. Mit Hilfe eines F-Tests kann die Signifikanz untersucht werden.
Zusätzlich drückt das Bestimmtheitsmaß aus, wie gut die gefundene Regressionsgerade den Zusammenhang von unabhängigen und abhängigen Variablen beschreibt.
Was ist ein F-Test?
Der F-Test ist eine statistische Prüfmethode, mit Hilfe derer überprüft werden kann, ob eine ermittelte Regression signifikant ist. Das bedeutet, dass überprüft wird, ob die aus der Stichprobe gewonnenen Erkenntnisse auch für die Gesamtheit der betrachteten Variablen gelten. Hierzu wird die Nullhypothese (alle Koeffizienten sind gleich null) angenommen. Kann diese nicht bestätigt werden, so ist die ermittelte Regression signifikant.
Übungsfragen
#1. Was versteht man unter der Regressionsanalyse?
#2. Was ist das Ziel der Regressionsanalyse?
#3. “Ist eine Regressionsgerade gefunden so ist automatisch klar, dass sich die Zusammenhänge auf die Gesamtheit der Variablen übertragen lässt” – Diese Aussage ist:
#4. “Um die Signifikanz der ermittelten Regression zu untersuchen, kann ein F-Test durchgeführt werden.” – Diese Aussage ist:
#5. “Die Regressionsanalyse kann für die Unterstützung der strategischen Planung im Unternehmen eingesetzt werden.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
