Beim Nash-Gleichgewicht handelt es sich um ein Konzept in der Spieltheorie, bei dem sich alle Spieler optimal verhalten, vorausgesetzt die Aktionen der anderen Spieler sind gegeben.
Du lernst in diesem Kapitel, was das Nash Gleichgewicht ist und wann es eine Rolle spielt. Wir zeigen dir außerdem, wie dieses Konzept angewendet werden kann und welche Vor- und Nachteile es mit sich bringt. Um dich auf deine nächste Prüfung vorbereiten zu können, helfen dir unsere Übungsaufgaben.
Warum ist das Nash Gleichgewicht wichtig?
Das Nash Gleichgewicht zeigt die für beide Spieler beste Strategieoption an. Vorausgesetzt, man kennt die Züge des anderen, kann von beiden Spielern die optimale Strategie genutzt werden. Dadurch profitieren beide Akteure am Markt, ohne kooperieren zu müssen.
Was ist das Nash Gleichgewicht?
Das Nash Gleichgewicht, nach seinem Begründer “John Forbes Nash“ benannt, ist eines der zentralen Elemente der Spieltheorie. In Spielen, bzw. Marktsituationen, in denen die Akteure nicht miteinander kooperieren, beschreibt das Nash Gleichgewicht genau die Strategiekombination, welche für alle Spieler die beste ist.
In dieser Situation ist es für keinen der Spieler sinnvoll, eine andere Strategie zu wählen, da er sich damit nicht besser stellen könnte. Die durch die Spieler gewählten Strategien sind die gegenseitig besten Antworten, weshalb die Spieler auch im Nachhinein mit der Wahl zufrieden sind und sich unter den gleichen Umständen wieder so entscheiden würden.
Beim Nash Gleichgewicht unterscheidet man zwischen drei verschiedenen Arten des Gleichgewichts:
- Nash Gleichgewicht in dominanten Strategien
- Nash Gleichgewicht in reinen Strategien
- Nash Gleichgewicht in gemischten Strategien
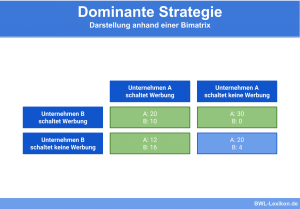
Nash Gleichgewicht in dominanten Strategien
Vom Nash Gleichgewicht in dominanten Strategien spricht man, wenn die Strategieauswahl des Spielers unabhängig von der Strategieauswahl des Gegenspielers erfolgt.
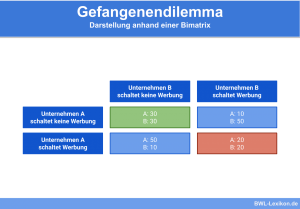
Bereits im Vorhinein legt sich der Spieler auf die für ihn dominante Strategie fest, sodass ein nicht unbedingt pareto-effizientes Gleichgewicht entsteht. Das bekannteste Beispiel für ein Nash Gleichgewicht bei dominanten Strategien ist das Gefangenendilemma.
Nash Gleichgewicht in reinen Strategien
Kennt der Spieler die gewählte Strategie seines Gegenspielers und antwortet darauf mit der für ihn besten Antwort, so spricht man von einem Nash Gleichgewicht in reinen Strategien. Voraussetzung dafür ist, dass wirklich ein Gleichgewicht entsteht, was bei reinen Strategien nicht immer der Fall sein muss.
Vorausgesetzt, Spieler B weiß im Vorfeld, wofür sich Spieler A entscheidet, so würde Spieler B immer die Strategie wählen, mit der er gewinnt, beispielsweise wählt Spieler A Schere, so wählt Spieler B Stein.
Weiß aber auch Spieler A, dass Spieler B Stein wählt, so würde er gar nicht Schere wählen. Somit kann bei diesen reinen Strategien nie ein Nash Gleichgewicht entstehen, da der Anreiz zur Wahl einer anderen Strategie immer gegeben ist, um den eigenen Nutzen zu erhöhen.
In reinen Strategien können aber auch ein oder mehrere Nash Gleichgewichte vorliegen. Um diese herauszufinden, konstruiert man den Zug eines Spielers und betrachtet die entsprechende Reaktion des Gegenspielers. Anschließend wird geschaut, ob der Spieler unter der Reaktion des Gegenspielers seinen eigenen Zug anders gestaltet hätte oder nicht. Bleibt er auch unter Berücksichtigung des Gegenzugs bei seiner gewählten Strategie, so handelt es sich um ein Nash Gleichgewicht.
Die entsprechenden Auszahlungen für die einzelnen Unternehmen sind in der folgenden Bimatrix dargestellt:
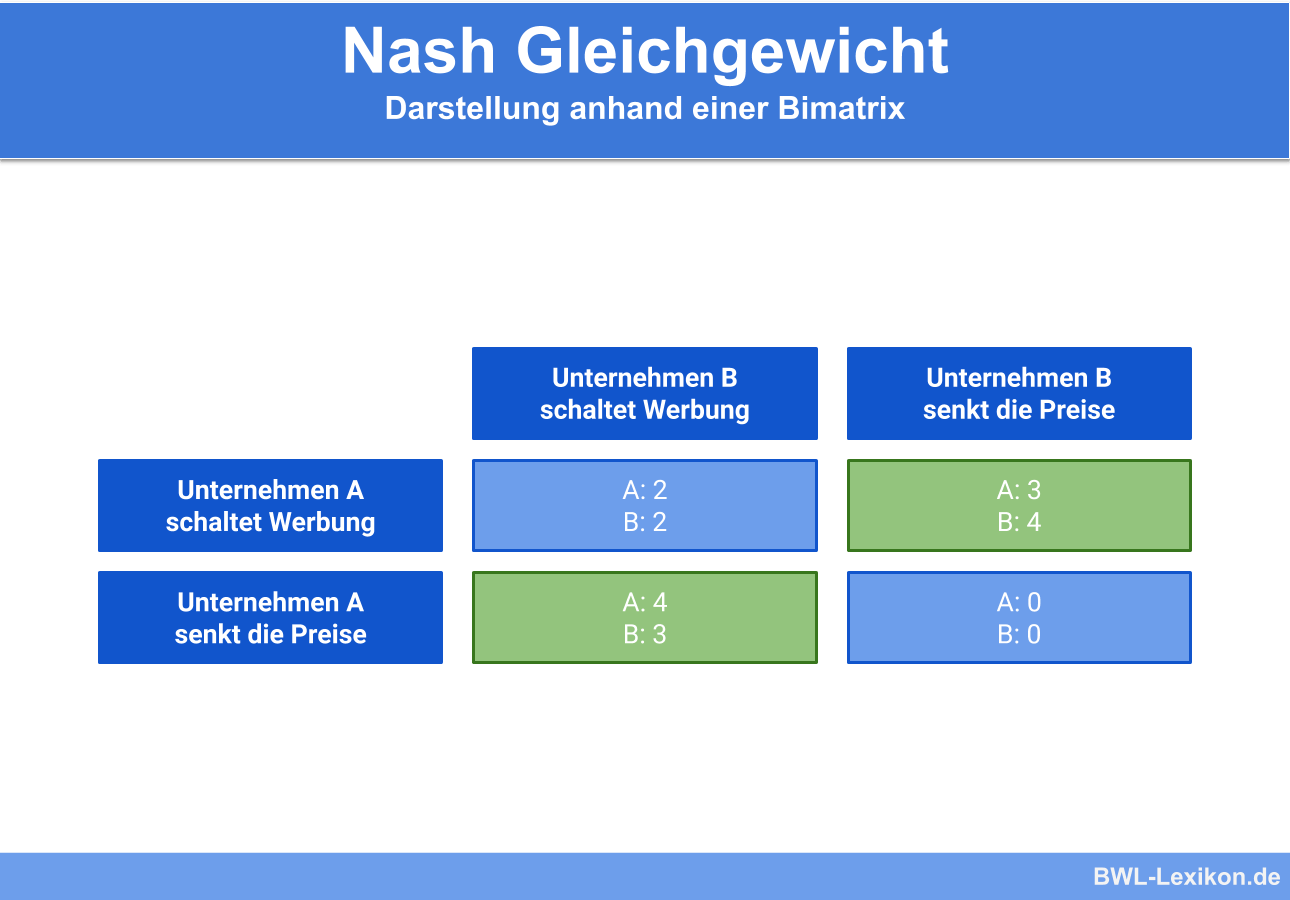
Entscheidet sich Unternehmen A also dafür, Werbung zu schalten, so ist die beste Option für Unternehmen B in diesem Falle keine Werbung zu schalten und stattdessen die Preise zu senken. Würde Unternehmen B zuerst die Preise senken, so ist es für Unternehmen A das beste Werbung zu schalten, um den höchsten Nutzen zu erzielen. Unternehmen A hat also auch unter dem Wissen der Reaktion von Unternehmen B auf seine Strategie des Werbung schaltens keinen Anreiz von dieser Strategie abzuweichen.
Gleiches gilt umgekehrt, wenn sich Unternehmen B zuerst entscheidet Werbung zu schalten und Unternehmen A daraufhin die Preise senkt. In diesem Fall hat auch Unternehmen B keinen Anreiz von seiner gewählten Strategie, die Umsätze mit zusätzlicher Werbung anzukurbeln, abzuweichen. Es liegen in diesem Fall also zwei Nash Gleichgewichte vor.
Nash Gleichgewicht in gemischten Strategien
Um das Nash Gleichgewicht in gemischten Strategien zu bestimmen, wird zusätzlich die Wahrscheinlichkeit der jeweiligen Strategieauswahl der Spieler berücksichtigt. In diesem Fall besitzt ein endliches Spiel mit gemischten Strategien im Gegensatz zu einem Spiel in reinen Strategien immer ein Nash Gleichgewicht.
Zur Bestimmung des Nash Gleichgewichts in gemischten Strategien wird also zuerst jeder Strategie der Spieler eine Wahrscheinlichkeit zugeordnet:
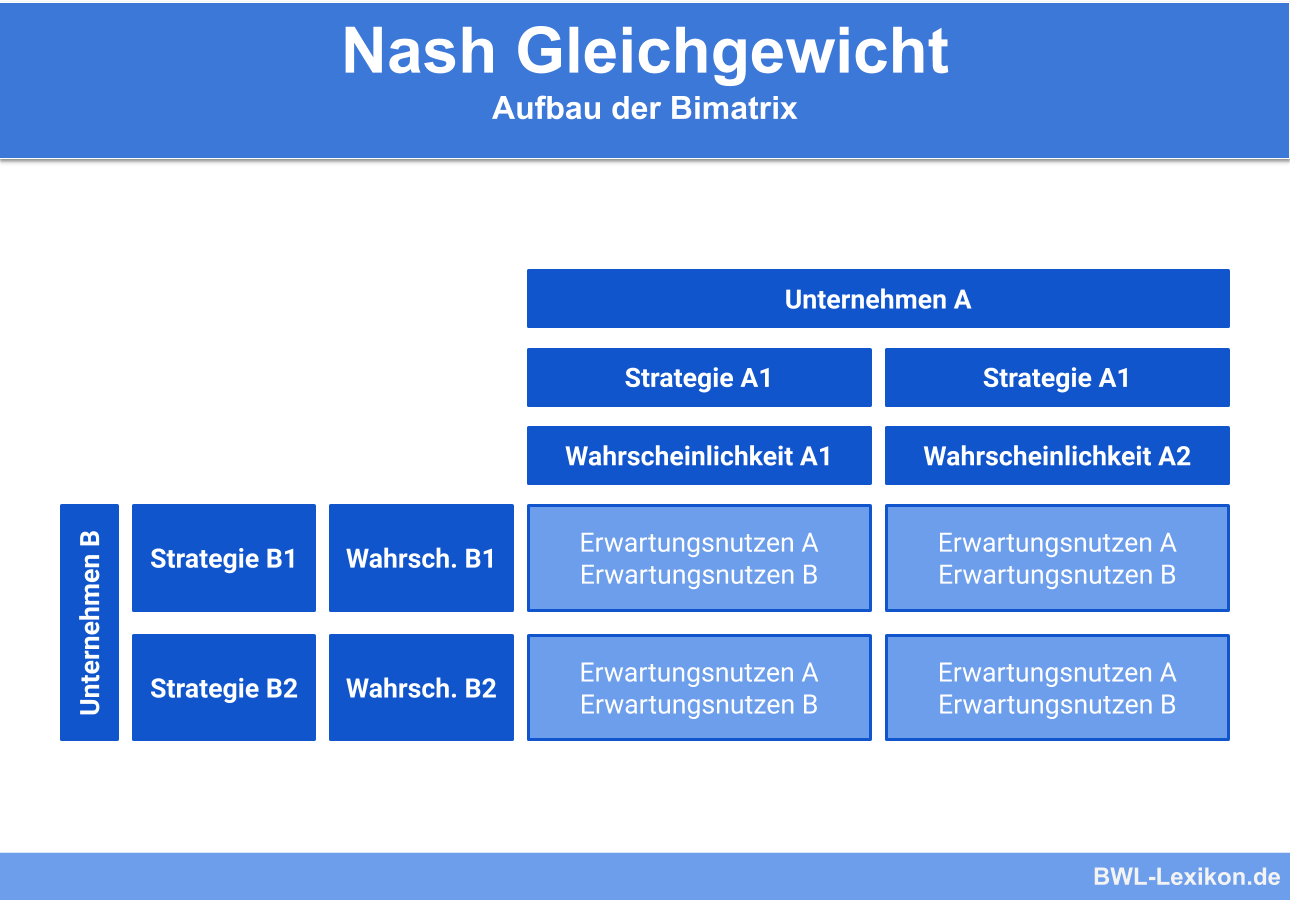
Um ein Nash Gleichgewicht zu erreichen, müssen die jeweiligen Erwartungsnutzen für die beiden Strategien des Spielers gleich sein. Hierzu werden die zu erwartenden Nutzen mathematisch gleichgesetzt.
Daraus ergibt sich folgende Bimatrix:
Der Erwartungs berechnet sich nun wie folgt:
Unternehmen A:
Werbung schalten = (2 * wb1) + (3 * (1-wb1))Preise senken = (4 * wb1) + (0 * (1-wb1))
Unternehmen B:
Werbung schalten = (2 * wa1) + (3 * (1-wa1))Preise senken = (4 * wa1) + (0 * (1-wa1))
Anschließend wird der Erwartungswert (E) nach der entsprechenden Wahrscheinlichkeit abgeleitet und die Gleichungen anschließend entsprechend umgestellt, um die jeweiligen Wahrscheinlichkeiten auszurechnen. Mit einsetzen der Auszahlungswerte in diese Gleichung kann das Nash Gleichgewicht errechnet werden.
Übungsaufgaben
#1. Was ist das Nash Gleichgewicht?
#2. Was ist einer der Vorteile des Nash Gleichgewichts?
#3. “Es existiert immer ein Nash Gleichgewicht, sowohl bei dominanten, bei reinen und bei gemischten Strategien”- Diese Aussage ist:
#4. “Es können auch mehrere Nash Gleichgewichte existieren.” – Diese Aussage ist:
#5. “Beim Nash Gleichgewicht hat keiner der Spieler einen Anreiz seine Strategie zu ändern.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
