Unter dem Begriff Spieltheorie versteht man eine mathematische Methode, die das Handeln der Akteure auf einem Markt als Spiel versteht. Mit ihr kann das rationale Verhalten in Entscheidungssituationen, welche nicht nur vom eigenen, sondern auch vom Verhalten anderer Akteure bestimmt wird, abgeleitet werden
Dieses Kapitel zeigt dir, was die Spieltheorie ist und wann sie eine Rolle spielt. Außerdem erläutern wir dir, wie du die Spieltheorie anwenden kannst und welche Vor- und Nachteile sie mit sich bringt. Damit du dein erworbenes Wissen zur Spieltheorie gleich testen kannst, haben wir einige Übungsaufgaben vorbereitet.
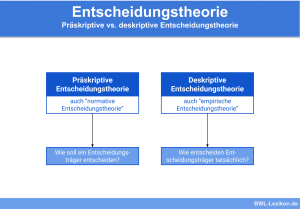
Synonyme: interaktive Entscheidungstheorie
Inhalt dieser Lektion
Warum ist die Spieltheorie wichtig?
Die Spieltheorie stellt komplexe Entscheidungssituationen, die abhängig vom Verhalten anderer Spielteilnehmer sind, vereinfacht dar. So lässt sich auch die Entscheidungsfindung vereinfachen. Hierzu dienen insbesondere die bereits erwähnten Lösungskonzepte, die wir in jeweils separaten Kapiteln behandeln.
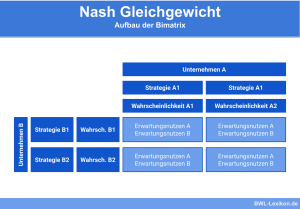
Die Bedeutung der Spieltheorie in der Wirtschaftswissenschaft macht die Vergabe des Nobelpreises in dieser Kategorie im Jahr 1994 deutlich. Dieser ging an John Forbes Nash, John Harsanyi und Reinhard Selten für Ihre Forschungen und Verdienste zur Weiterentwicklung der Spieltheorie. Das bekannteste Konzept hieraus ist das Nash-Gleichgewicht.
Was ist die Spieltheorie?
Die Spieltheorie wird angewendet, um das Verhalten von Unternehmen im Wettbewerb auf dem Markt zu untersuchen. Die einzelnen Akteure auf dem Markt werden dabei als „Spieler“ wie in einem Brettspiel angesehen, deren Handlungen und Entscheidungen in Abhängigkeit von den Handlungen und Entscheidungen der anderen Spieler stehen.
Um Entscheidungen zu treffen und Strategien festzulegen, müssen die Spieler dabei immer die Aktionen und Reaktionen der Mitspieler auf dem Markt berücksichtigen.
Bei der Spieltheorie handelt es sich um eine vereinfachte und abstrakte Form, das strategische Denken von Marktakteuren darzustellen. Im Rahmen eines Spiels kann die Entscheidungsfindung vereinfacht analysiert werden.
Dabei gibt es immer mindestens zwei Akteure in einem Spiel, um die Interaktion untereinander zu ermöglichen. Unter bestimmten Spielregeln können die jeweiligen Spieler in Folge ihrer Entscheidungen etwas verlieren oder gewinnen.
Kooperative und nicht kooperative Spieltheorie
Unterscheiden kann man die Spieltheorie in die Unterpunkte:
- kooperative Spieltheorie:
- Spieler können untereinander bindende Verträge abschließen
- besitzt eine Koalitionsfunktion und ist auszahlungsorientiert
- bekannteste Konzepte: Kern, Shapley-Lösung, Nash-Verhandlungslösung
- alle Handlungen der Spieler ergeben sich aus dem eigenen Interesse, ohne bindende Verträge abzuschließen
- ist aktions- und strategieorientiert
Anwendung der Spieltheorie
In der Spieltheorie werden verschiedenste Situationen als Spiel modelliert. Dabei wird festgelegt, welche Spieler, welchen Ablauf und welche Handlungsalternativen bzw. Spielzüge den einzelnen Spielern zur Verfügung stehen.
Außerdem wird eine bestimmte Auszahlungsfunktion festgelegt, welche jedem möglichen Ausgang des Spiels einen bestimmten Auszahlungsvektor zuordnet. Dieser beschreibt, wie hoch der Gewinn eines jeden Spielers bei einem bestimmten Spielausgang ist.
Für unterschiedlichste Spielsituationen gibt es entsprechende Lösungskonzepte. Die bekanntesten sind:
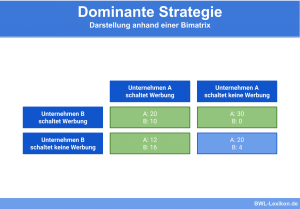
- Dominante Strategie
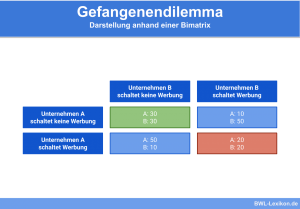
- Gefangenendilemma
- Nash-Gleichgewicht
Zur Darstellung der Spieltheorie können genutzt werden:
- Normalform:
- Darstellung in einer Bimatrix
- wird bei statischen Spielen verwendet, d.h. die Spieler treffen Ihre Entscheidungen gleichzeitig
- Extensivform:
- Darstellung in einem Spielbaum
- wird bei dynamischen Spielen verwendet, d.h. die Spieler treffen Ihre Entscheidungen nacheinander
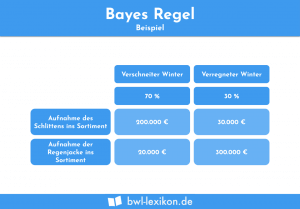
Beispiel für die Normalform als Bimatrix
Unternehmen A möchte seinen Marktanteil erhöhen und überlegt dafür die Verkaufspreise zu senken, um mehr Kunden anzulocken.
Der größte Konkurrent, Unternehmen B, könnte allerdings ebenfalls die Preise senken.
Im Sinne der Spieltheorie wird folgende Bimatrix aufgestellt, in der die jeweiligen zu erwartenden Ergebnisse der Umsatzentwicklung für die Unternehmen eingetragen werden:
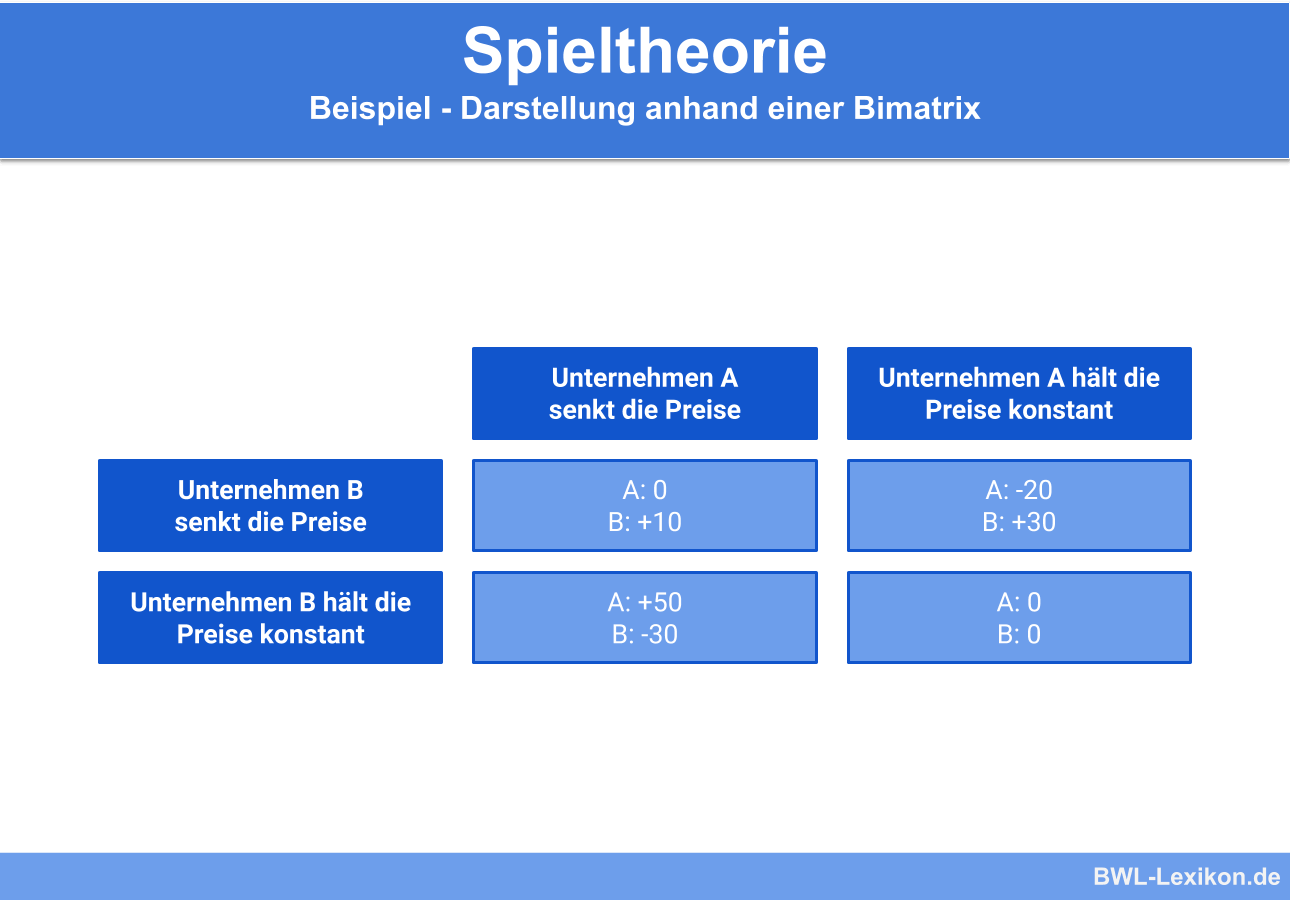
Der erste Wert steht dabei für die zu erwartende Entwicklung bei Unternehmen B, die zweite für Unternehmen A. Anhand der Bimatrix, auch Auszahlungsmatrix genannt, kann man erkennen, dass die jeweiligen Ergebnisse vom Handeln des anderen Spielers abhängig sind. Um die bestmögliche Strategie zu wählen, stehen die genannten unterschiedlichen Lösungskonzepte zur Verfügung.
Beispiel für die Extensivform als Spielbaum
Nehmen wir in unserem Beispiel an, dass Unternehmen A zuerst handelt und Unternehmen B darauf reagieren muss.
Um dies in der Form der Spieltheorie darzustellen, ist der Spielbaum am besten geeignet:
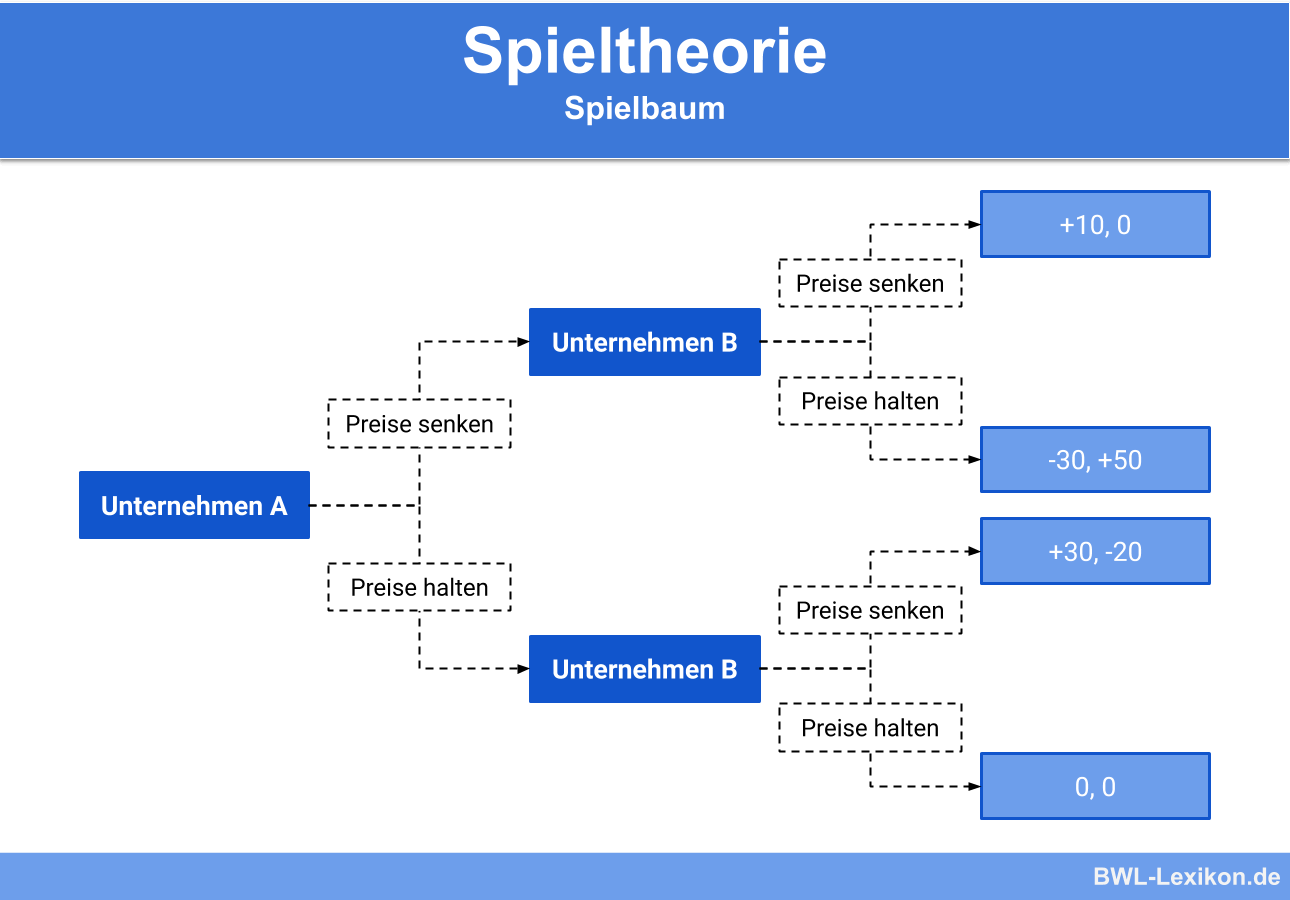
Durch den Spielbaum wird die zeitliche Komponente in dem Spiel berücksichtigt, da die Reaktion von Unternehmen B erst in Folge der Aktion von Unternehmen A entsteht. Am Ende eines jeden möglichen Entscheidungsastes stehen die zu erwartenden Ergebnisse.
Der Einfachheit halber werden die Beobachtungen aus dem Spielbaum nun in eine Tabelle eingetragen, in der die möglichen Handlungszusammenhänge und -kombinationen dargestellt werden können:
| B1 | B2 | |
| A1 | +10; 0 | -30; +50 |
| A2 | +30; -20 | 0; 0 |
Dabei stehen die Abkürzungen für folgende Handlungsoptionen:
- A1: Unternehmen A senkt die Preise.
- A2: Unternehmen A hält die Preise stabil.
- B1: Unternehmen B senkt die Preise.
- B2: Unternehmen B hält die Preise stabil.
Anhand der Tabellenform lassen sich nun wieder die entsprechenden Lösungskonzepte anwenden, die zur optimalen Strategie führen.
Vorteile und Nachteile der Spieltheorie
- Die Spieltheorie stellt komplexe strategische Entscheidungssituationen, in denen sich die Strategien der einzelnen Akteure untereinander bedingen, in vereinfachter Form dar.
- Anhand der der Spieltheorie zugehörigen Lösungskonzepte kann die Entscheidungsfindung vereinfacht werden.
- Die Spieltheorie setzt rationales Verhalten aller Spielteilnehmer voraus, was in der Realität nicht immer gegeben sein muss.
