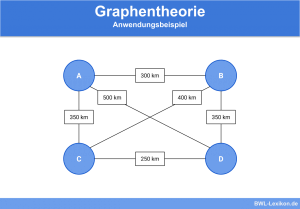
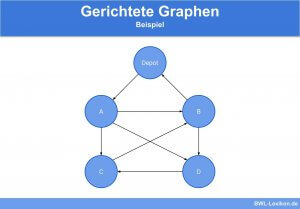
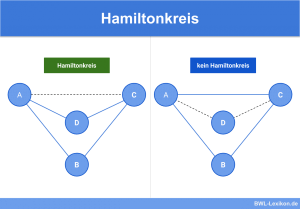
Die ungarische Methode wird in der linearen Optimierung angewendet, speziell zur Lösung von gewichteten Zuordnungsproblemen in bipartiten Graphen.
Wir zeigen dir im folgenden Kapitel, was die ungarische Methode ist und wie sie angewendet wird. Außerdem erläutern wir dir, warum die ungarische Methode wichtig ist. Mit unseren Übungsaufgaben kannst du zum Abschluss deinen Wissensstand überprüfen.
Synonym: Kuhn-Munkres-Algorithmus
Warum ist die ungarische Methode wichtig?
Mit der ungarischen Methode können lineare Optimierungsprobleme gelöst werden, die bei gewichteten Zuordnungen in bipartiten Graphen entstehen. Mit ihr kann die eindeutige Zuordnung von Objekten aus zwei Gruppen so optimiert werden, dass die Gesamtkosten minimiert werden bzw. der Gesamtgewinn maximiert werden kann. Dies kann in unterschiedlichsten Fällen der betrieblichen Praxis der Fall sein, beispielsweise bei der Abstimmung von Dienst- und Urlaubsplänen oder auch in der Logistikplanung.
Was versteht man unter der ungarischen Methode?
Die ungarische Methode ist ein Algorithmus zur Lösung linearer Optimierungsprobleme. Um dies zu erreichen, wird zuerst die Ausgangsmatrix reduziert. Dabei werden sowohl die Spaltenelemente um das Spaltenminimum als auch die Zeilenelemente um das Zeilenminimum reduziert.
Anschließend erfolgt die Zuordnung. Dafür wird zuerst eine Zelle mit dem Eintrag “0” gesucht, die in keiner weiteren Zeile oder Spalte eine Null aufweist. Auch bei den weiteren Zuordnungen muss beachtet werden, dass jede Zeile und jede Spalte immer genau eine eindeutige Zuordnung ergibt. Die optimale Lösung ist erreicht, wenn genau n Zuordnungen gefunden sind.
Beispiel: Anwendung der ungarischen Methode
Dazu muss immer jeweils ein Kollege am Sonntag arbeiten, wobei sich innerhalb eines Monats alle abwechseln. Zu Beginn des Monats wird der Dienstplan erstellt, bei dem jeder seine Präferenzen angeben kann, an welchem Sonntag er arbeiten möchte.
Diese werden in folgender Matrix eingetragen:
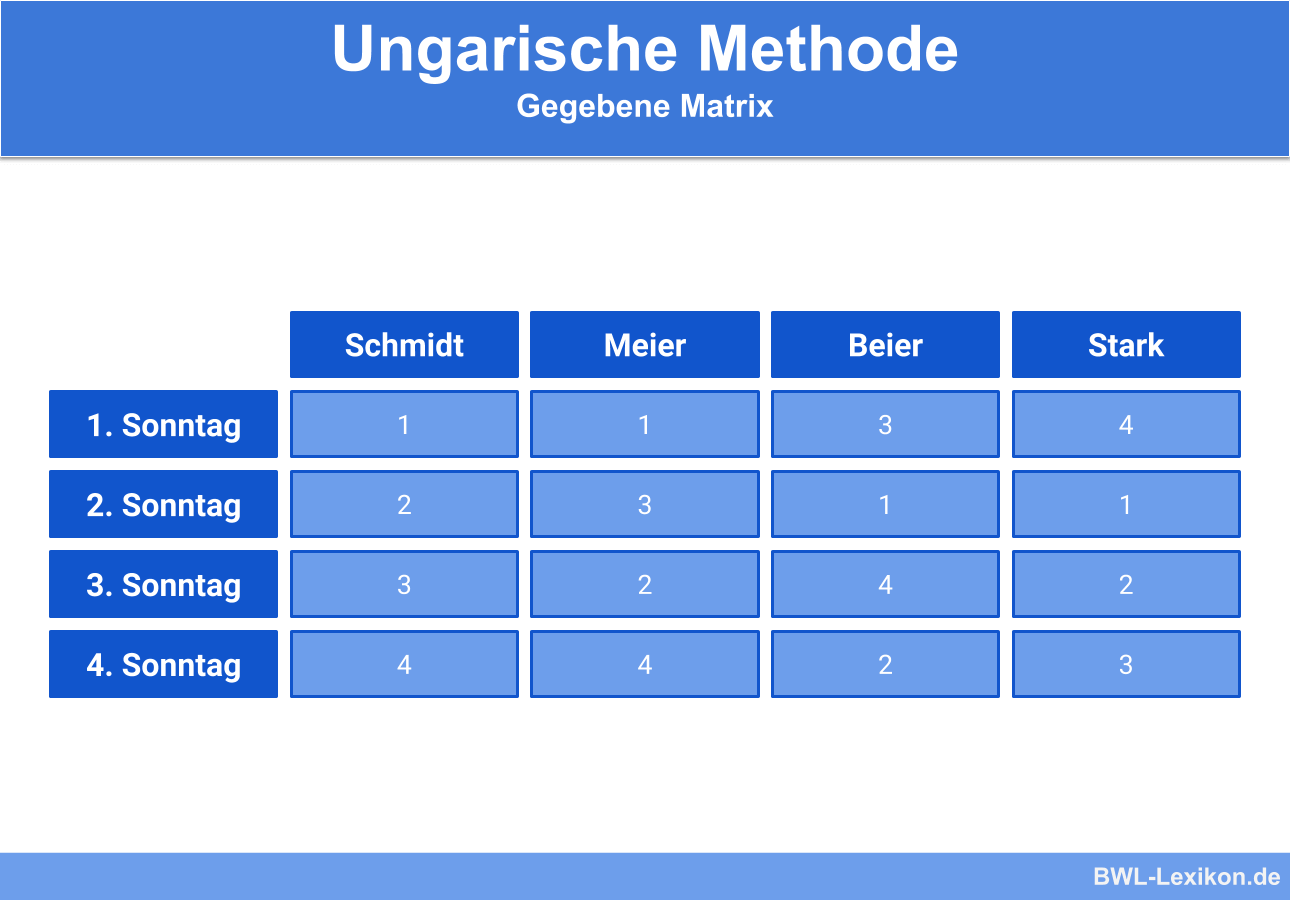
Eine 1 steht dabei für die höchste Präferenz, eine 4 für die niedrigste Präferenz.
Anschließend wird mit der Reduktion der Spaltenelemente um das Spaltenminimum begonnen. Das bedeutet: Alle Einträge in den Spalten werden um das Minimum reduziert. Da 1 in jeder Spalte das Minimum darstellt, wird von allen Einträgen 1 subtrahiert.
So erhalten wir folgende Matrix:
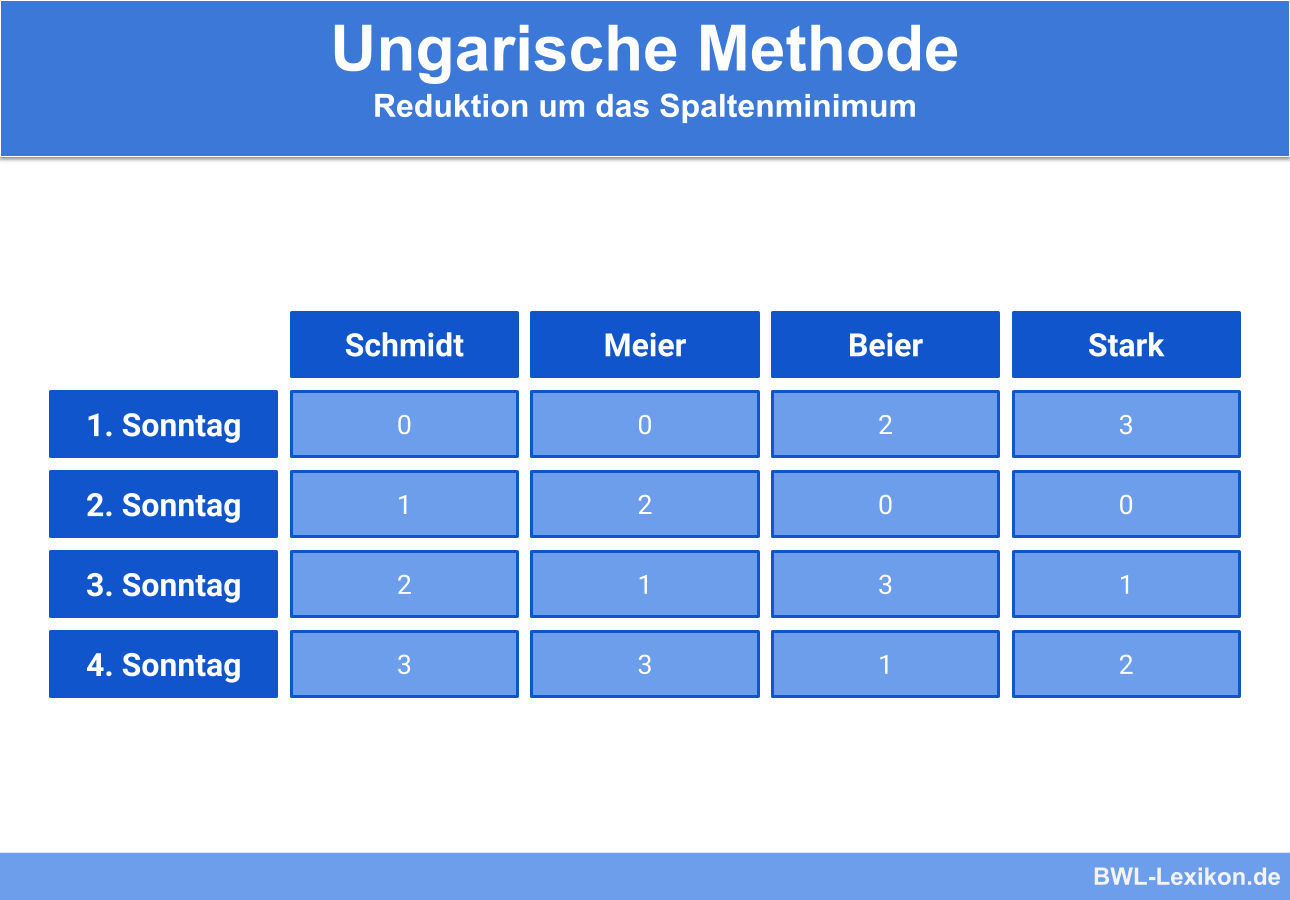
Anschließend werden analog dem vorherigen Vorgehen die Zeilenelemente um das jeweilige Zeilenminimum reduziert.
So ergeben sich folgende Einträge in der Matrix:
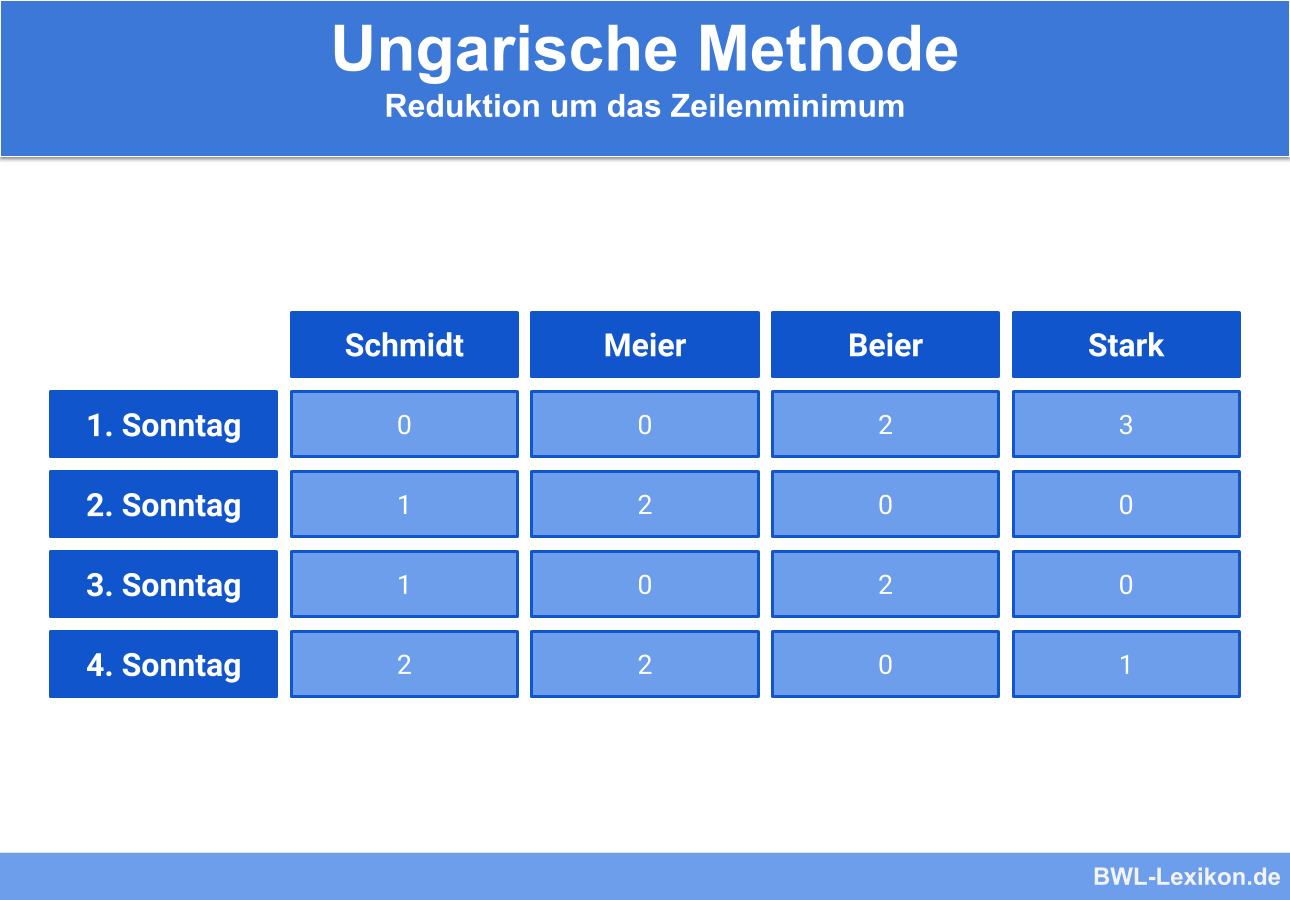
Sind sowohl Spalten- als auch Zeilenelemente entsprechend reduziert, erfolgt die Zuordnung. Dafür wird zuerst nach einer Zeile oder Spalte gesucht, in der nur eine null enthalten ist. In unserem Beispiel sehen wir, dass die Spalte “Kollege Schmidt” nur eine Null enthält.
Diese können wir uns markieren:
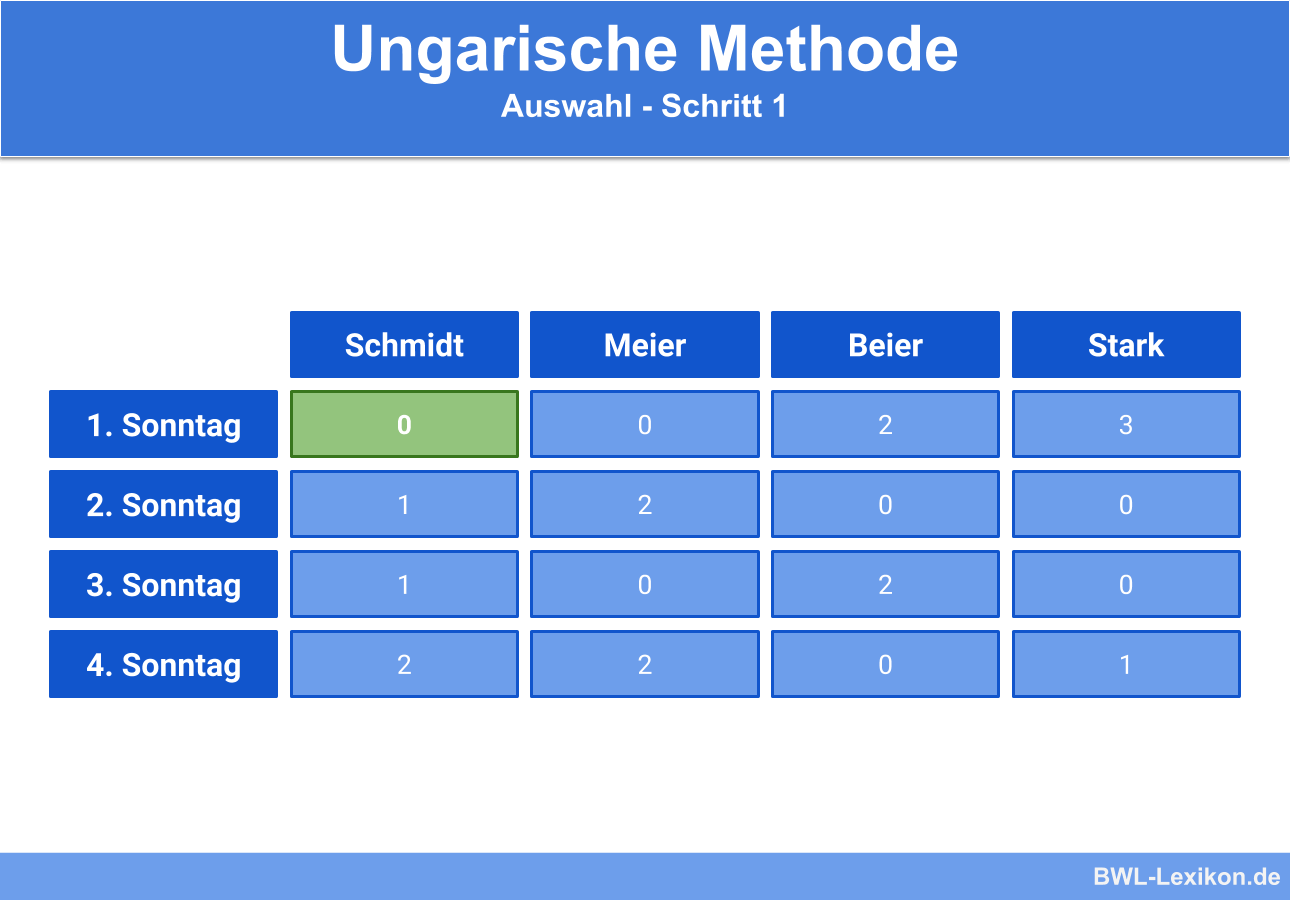
Da in jeder Zeile und spalte für die Anwendung der ungarischen Methode immer nur eine null enthalten sein darf, können wir die zweite null in der Zeile “1. Sonntag” streichen:
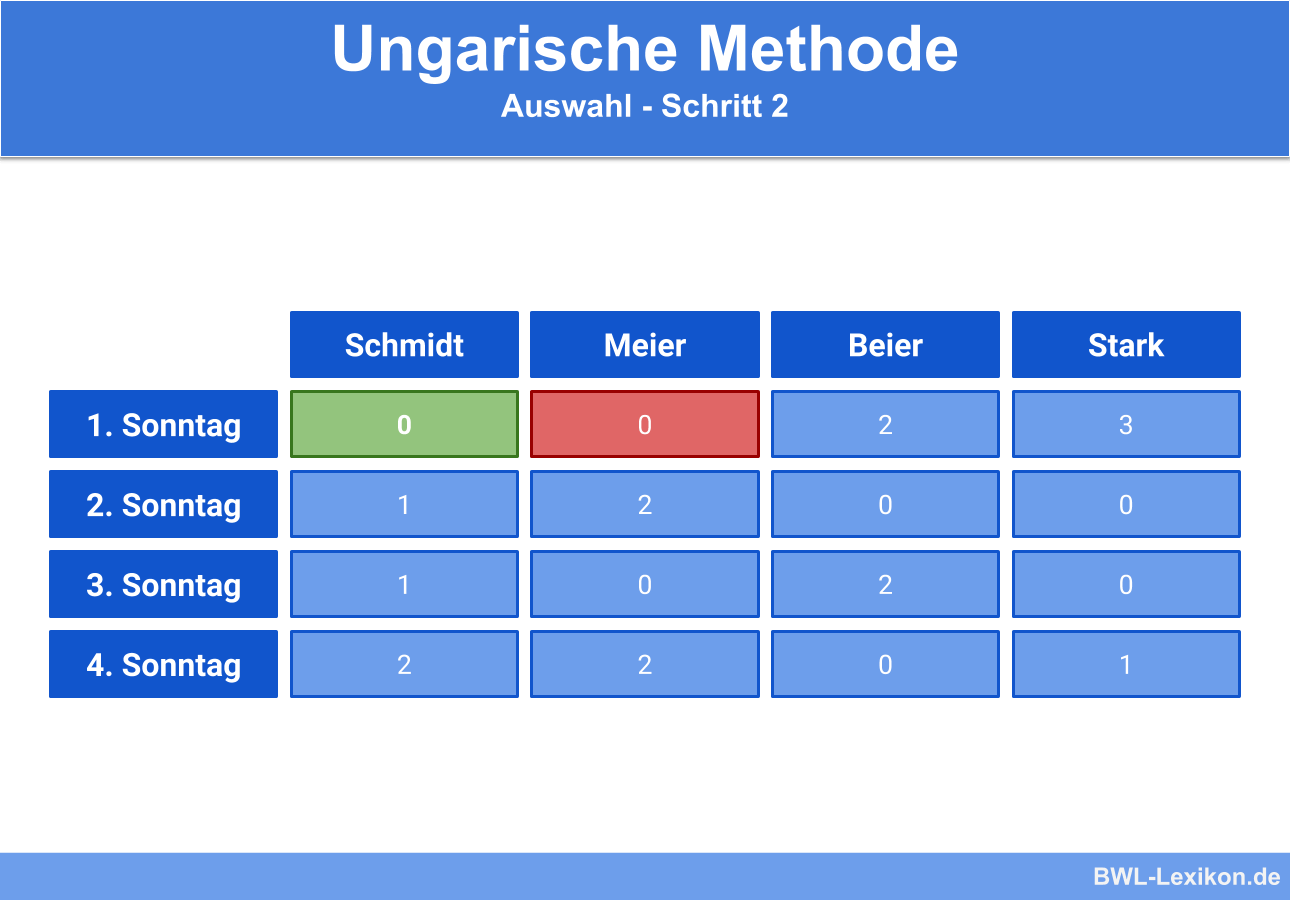
Dadurch bleibt in der Spalte “Kollege Meier” nur ein Eintrag mit null übrig. Dieses Vorgehen wiederholen wir analog bei den weiteren Zeilen und Spalten.
So erhalten wir:
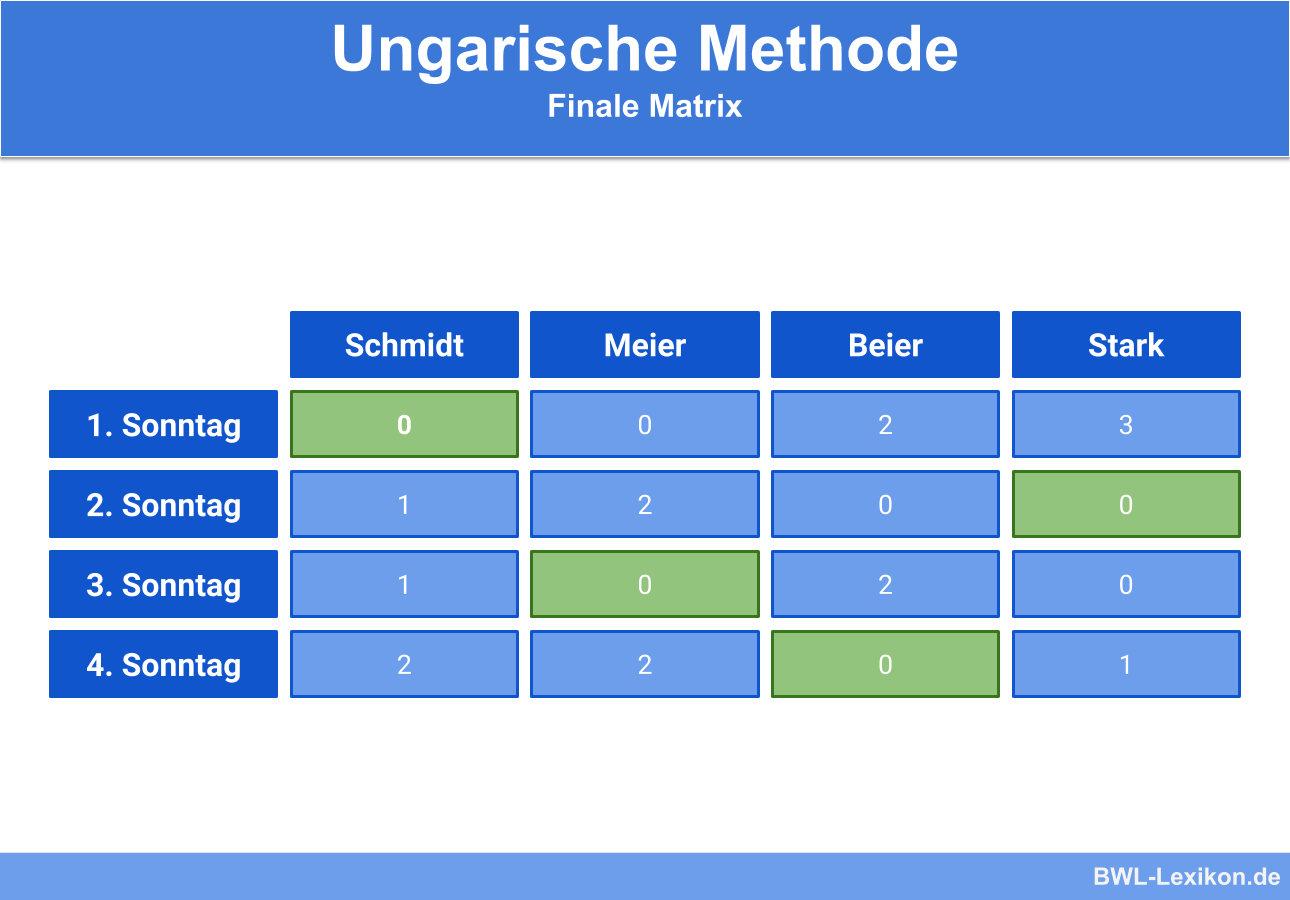
Anhand der markierten Einträge können wir nun erkennen, an welchem Tag wer arbeiten muss, damit die persönlichen Präferenzen bestmöglich erfüllt werden:
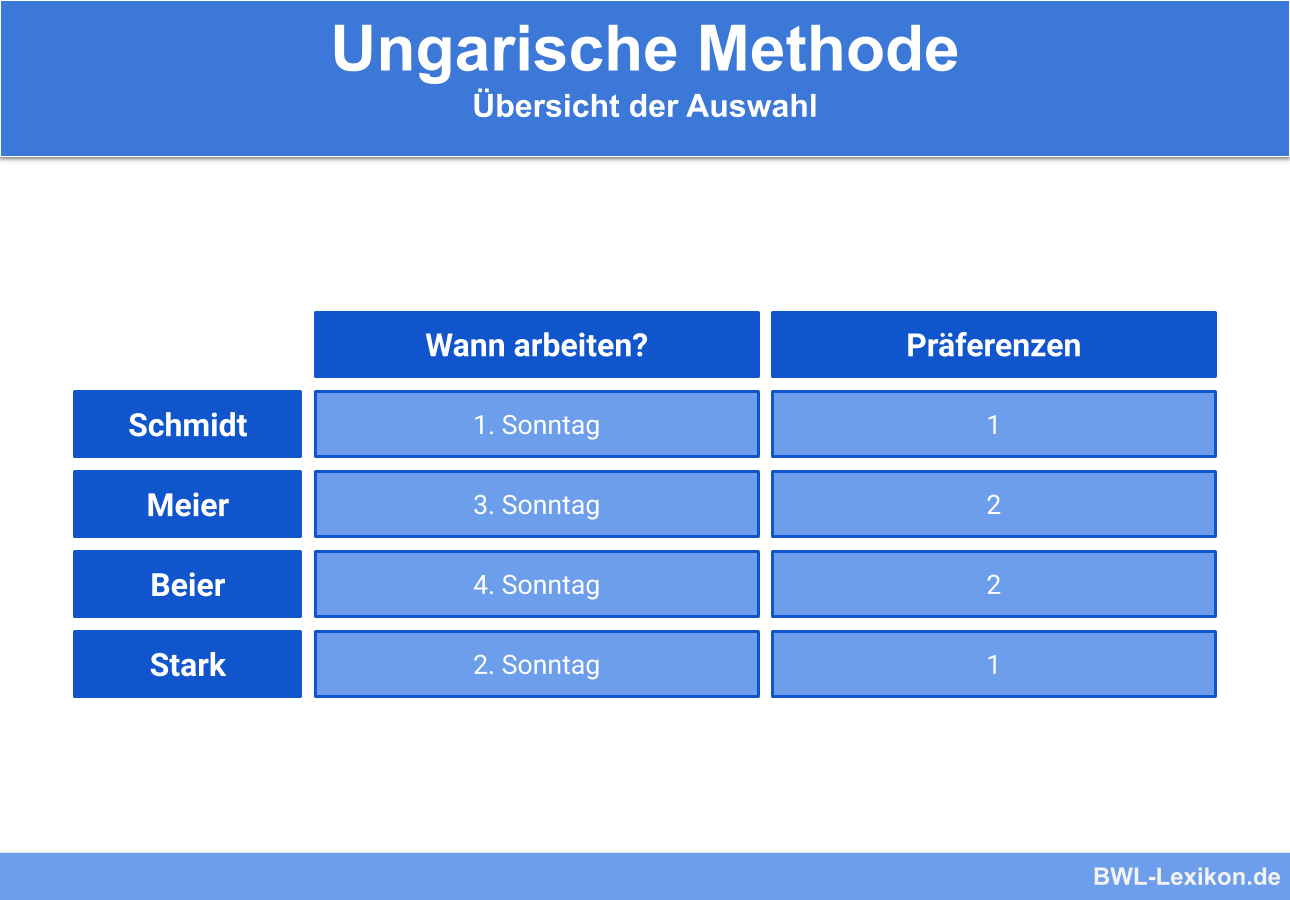
Die bestmögliche Arbeitsaufteilung unter Berücksichtigung der persönlichen Präferenzen der Angestellten ist nun dank der ungarischen Methode gefunden. Mit dieser Lösung können sich alle arrangieren und die Kunden erhalten jeden Sonntag im Monat frische Brötchen.
Übungsfragen
#1. Was versteht man unter der ungarischen Methode?
#2. Wie wird die ungarische Methode angewendet?
#3. “Die ungarische Methode dient der Lösung von Zuordnungsproblemen in nicht bipartiten Graphen.” – diese Aussage ist:
#4. “Mit der ungarischen Methode kann die Zuordnung von Elementen zweier Gruppen in einem Graphen optimiert werden.” – Diese Aussage ist:
#5. “Die optimale Lösung des Zuordnungsproblems ist erreicht, wenn durch die ungarische Methode genau n Zuordnungen gefunden wurden.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
