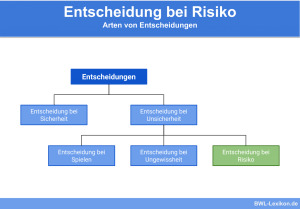
Das Bernoulli-Prinzip beschreibt eine Entscheidungsregel bei Entscheidungen unter Risiko. Demnach werden rationale Entscheidungen unter Berücksichtigung der Risikofreudigkeit des Entscheiders anhand des zu erwartenden Nutzenwertes getroffen.
Du wirst in diesem Kapitel erfahren, was genau man unter dem Bernoulli-Prinzip versteht, wie es funktioniert und welche Bedeutung es hat. Zudem stellen wir dir Übungsaufgaben zur Verfügung, mit denen du überprüfen kannst, ob du in diesem Thema fit für deine nächste Prüfung bist.
Welche Bedeutung hat das Bernoulli-Prinzip?
Der schweizer Mathematiker und Physiker Daniel Bernoulli entwickelte das nach ihm benannte Prinzip als Entscheidungsregel für Entscheidungen unter Risiko als Lösung zum Problem des Petersburger Paradoxons, welches sich mit den Entscheidungen bei einer Lotterie auseinandersetzt.
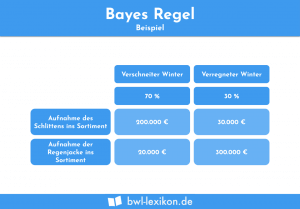
Das Bernoulli-Prinzip soll Entscheidungsträgern die Entscheidung in Situationen unter Risiko erleichtern, bzw. solche Entscheidungsprozesse erklären. Im Gegensatz zur Bayes-Regel bezieht das Bernoulli-Prinzip auch die individuelle Risikofreudigkeit des Entscheiders mit in die Nutzenfunktion ein.
Da das Bernoulli-Prinzip von J. von Neumann und O. Morgenstern axiomatisch fundiert werden konnte, gilt es heutzutage als eine der wichtigsten normativen Entscheidungsregeln und wird dementsprechend häufig in der wirtschaftswissenschaftlichen Theorie angewendet.
In der betrieblichen Praxis erkennt man aber häufig, dass Entscheidungen nicht immer rein rational getroffen werden. Hier kommen andere Entscheidungstheorien ins Spiel, beispielsweise die Prospect Theorie.
Was versteht man unter dem Bernoulli-Prinzip?
Das Bernoulli-Prinzip ist eine Entscheidungsregel für Entscheidungen unter Risiko.
Nach dem Bernoulli-Prinzip erfolgt das Treffen von Entscheidungen in solchen Situation in zwei Schritten:
- Im ersten Schritt ermittelt man die subjektive Vorstellung des Nutzens der einzelnen Handlungsalternativen für den Entscheider.
- Anschließend trifft der Entscheider eine Auswahl zwischen den Handlungsalternativen, welche ihm den höchsten erwarteten Nutzen einbringen wird.
Um den entsprechenden Präferenzwert zu ermitteln, wird folgende Formel genutzt:
![\[ \Phi (A_a) = E[U(\tilde{x}_a)] = \sum_{x_a}w(x_a)*U(x_a) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-568d5b98930d3e47c076fbb13877b52c_l3.png "Rendered by QuickLaTeX.com")
Aa bezeichnet dabei die Alternative a, deren mögliche Ergebnisse xa sind. Die Wahrscheinlichkeit des Eintretens eines Ereignisses wird mit w(xa) beschrieben. Der Nutzenwert des möglichen Ergebnisses wird als U(xa) bezeichnet.
Die Entscheidungsregel, die den eigenen Nutzenwert maximiert, lautet demnach:
![\[ \max_{a} \Phi (A_a) = \max_{a}~E[U(\tilde{x}_a)] \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-fdb622c6cbc781e89d591b5da5b2ef89_l3.png "Rendered by QuickLaTeX.com")
Die Handlungsalternativen für Herrn Maier sind folgende:
- a1 = in Aktien investieren
- a2 = nicht in Aktien investieren
Wenn Herr Meier nicht in Aktien investiert, bleibt sein Geldbetrag gleich. Legt er dagegen das Geld in Aktien an, kann der Kurs um 20 % steigen (Umweltzustand 1 = s1), um 20 % fallen (Umweltzustand 2 = s2) oder konstant bleiben (Umweltzustand 3 = s3).
- w1=50 %
- w2=30 %
- w3=20 %
Herr Meier ist risikoscheu, das bedeutet seine Nutzenfunktion ist konkav und kann folgendermaßen dargestellt werden:
![\[ u(e_{ij}) = \sqrt{e_{ij}} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-eee765db992edfa19e3d82b4487664b4_l3.png "Rendered by QuickLaTeX.com")
Um sich einen Überblick über den Erwartungsnutzen der Handlungsalternativen zu verschaffen und eine Entscheidung nach dem Bernoulli-Prinzip treffen zu können, wird folgende Matrix erstellt:
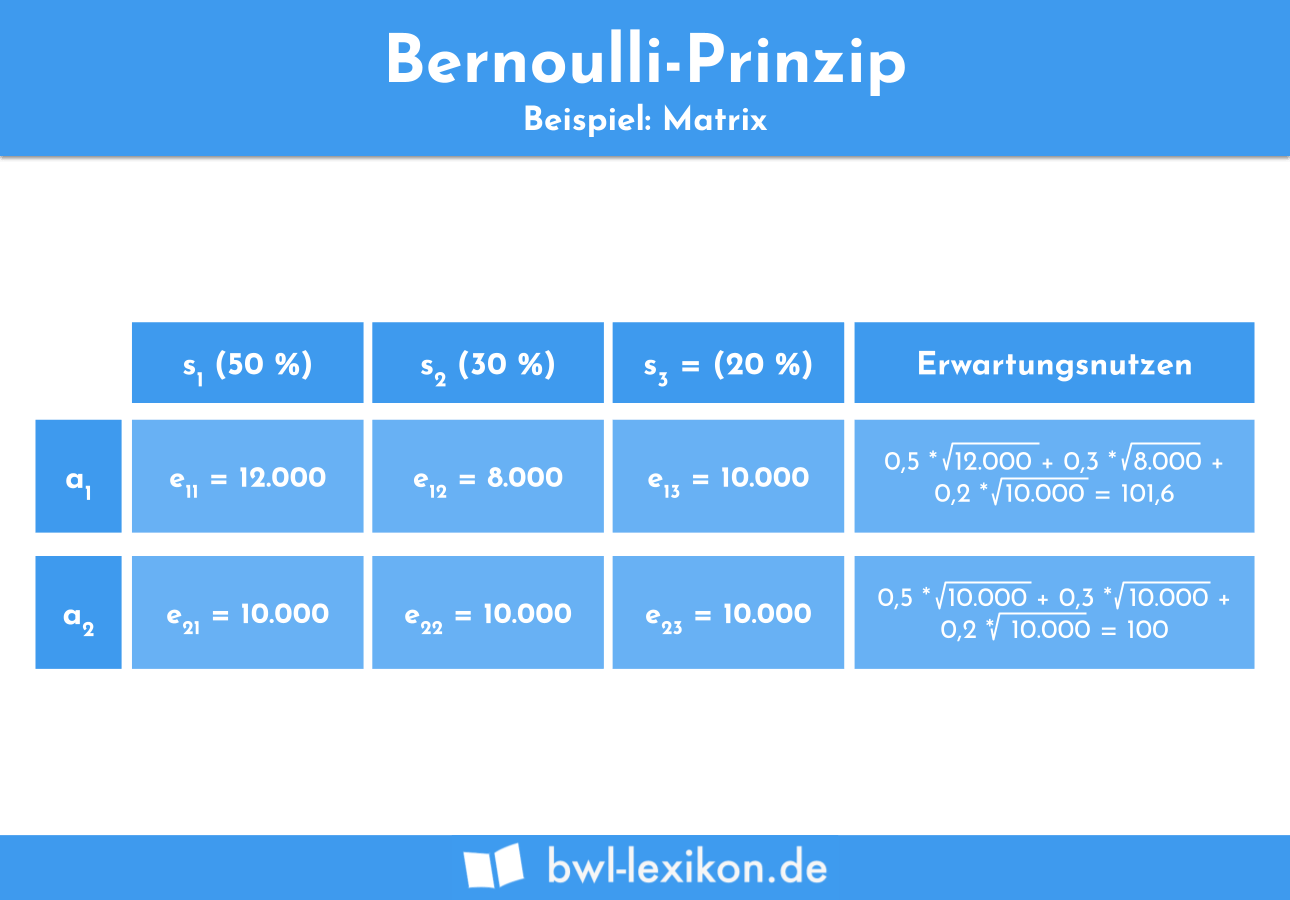
Der erwartete Nutzen liegt bei Handlungsalternative 1 höher als bei Handlungsalternative 2. Herr Meier wird sich demnach entscheiden, das geerbte Vermögen in Aktien zu investieren.
Übungsfragen
#1. Was versteht man unter dem Bernoulli-Prinzip?
#2. Wie werden Entscheidungen nach dem Bernoulli-Prinzip getroffen?
#3. “Das Bernoulli-Prinzip soll helfen, rationale Entscheidungen in Situationen unter Risiko zu erleichtern.” – Diese Aussage ist:
#4. “Beim Bernoulli-Prinzip wird die individuelle Risikoaffinität des Entscheiders nicht berücksichtigt.” – Diese Aussage ist:
#5. “Das Bernoulli-Prinzip als Entscheidungstheorie versucht zu erklären, warum in realen Entscheidungssituationen oft auch irrationale Entscheidungen getroffen werden.” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
