Eine Entscheidung bei Risiko besteht dann, wenn im Vorfeld einer Entscheidungssituation die Wahrscheinlichkeiten für das Eintreten der jeweiligen Umweltzustände bekannt sind.
Du erfährst in diesem Kapitel, was die Entscheidung bei Risiko bedeutet und wann sie eine Rolle spielt. Außerdem zeigen wir dir mögliche Entscheidungsregeln für Entscheidungen bei Risiko. Mithilfe unserer Übungsaufgaben kannst du dein Wissen zu Entscheidungen bei Risiko überprüfen.
Warum sind Entscheidungen bei Risiko wichtig?
Entscheidungen bei Risiko können für Unternehmen weitreichende wirtschaftliche Folgen haben. Dementsprechend ist es wichtig, fundierte Entscheidungen treffen zu können. Dazu liegen verschiedene Entscheidungsregeln zugrunde.
Was bedeutet Entscheidung bei Risiko?
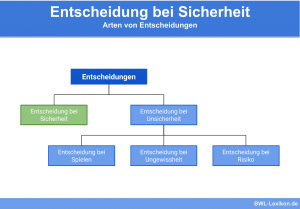
Jeden Tag müssen in Unternehmen Entscheidungen getroffen werden. In der Entscheidungstheorie unterscheidet man folgende Arten von Entscheidungen:
Entscheidungen unter Risiko zeichnet aus, dass die zu erwartenden Umstände mit unterschiedlichen Wahrscheinlichkeiten eintreten werden. Diese Eintrittswahrscheinlichkeiten sind dem Entscheidungsträger im Vorfeld bekannt.
In der unternehmerischen Praxis handelt es sich bei den meisten Entscheidungen um Entscheidungen unter Ungewissheit oder um Entscheidungen bei Risiko. Um aus einer Entscheidungssituation unter Ungewissheit eine bei Risiko zu machen, können die Eintrittswahrscheinlichkeiten der zu erwartenden Umweltzustände beispielsweise mittels Marktforschungsinstrumenten herausgefunden werden.
Die Entscheidungssituation bei Risiko wird in einer Ergebnismatrix dargestellt:
| Eintrittswahrscheinlichkeit 1 | Eintrittswahrscheinlichkeit 2 | |
| Umweltzustand 1 | Umweltzustand 2 | |
| Handlungsalternative 1 | Ergebnis aus Handlung 1 bei Umweltzustand 1 | Ergebnis aus Handlung 1 bei Umweltzustand 2 |
| Handlungsalternative 2 | Ergebnis aus Handlung 2 bei Umweltzustand 1 | Ergebnis aus Handlung 2 bei Umweltzustand 2 |
Anhand seiner Erfahrungswerte aus den letzten Jahren kann er folgende Annahmen zum Absatz treffen:
- Bei gutem Wetter verkauft er 200 Bratwürste am Eröffnungstag.
- Bei bewölktem Wetter verkauft er 100 Bratwürste am Eröffnungstag.
- Bei regnerischem Wetter verkauft er 50 Bratwürste am Eröffnungstag.
Einkaufspreise / Verkaufspreise:
- Im Einkauf kostet ihn eine Bratwurst 1,00 €.
- Der Verkaufserlös liegt bei 3,00 €.
Der Wetterbericht sagt folgende Wahrscheinlichkeiten voraus:
- gutes Wetter: 20 %
- bewölktes Wetter: 50 %
- regnerisches Wetter: 30 %
Die zu erzielenden Gewinne stellen die möglichen Ergebnisse dar. Um zu entscheiden, wieviel Bratwürste er einkaufen soll, stellt er folgende Ergebnismatrix auf:
| w1 = 20 % | w2 = 50 % | w3 = 30 % | |
| z1 = gutes Wetter | z2 = bewölktes Wetter | z3 = regnerisches Wetter | |
| a1 = Kaufe 200 Bratwürste ein | Gewinn = 400 € | Gewinn = 100 € | Gewinn = -50 € |
| a2 = Kaufe 100 Bratwürste ein | Gewinn = 200 € | Gewinn = 200 € | Gewinn = 50 € |
| a3 = Kaufe 50 Bratwürste ein | Gewinn = 100 € | Gewinn = 100 € | Gewinn = 100 € |
Um anhand dieser Ergebnismatrix die beste Entscheidung treffen zu können, stehen dem Pächter unterschiedliche Entscheidungsregeln zur Verfügung.
Unterschiedliche Entscheidungsregeln für Entscheidungen bei Risiko
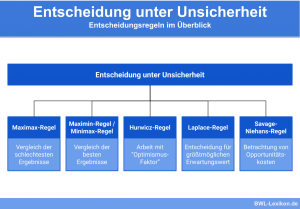
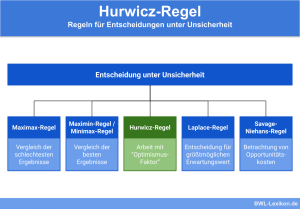
Für Entscheidungen bei Risiko stehen dem Entscheidungsträger unterschiedliche Entscheidungsregeln zur Verfügung:
- die Bayes-Regel
- das Bernoulli-Prinzip
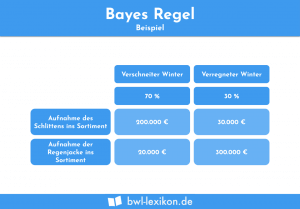
Die Bayes-Regel
Trifft der Entscheidungsträger seine Entscheidung nach der Bayes-Regel, so orientiert er sich an den jeweiligen Erwartungswerten der einzelnen Handlungsalternativen. Aus diesem Grund ist die Bayes-Regel auch als Erwartungswert-Prinzip bekannt. Die Bayes-Regel geht davon aus, dass der Entscheider risikoneutral ist.
Die Berechnung des Erwartungswerts der einzelnen Handlungsalternative ergibt sich aus der Gesamtsumme der Produkte aus Ergebnis und Wahrscheinlichkeit:
![\[ Erwartungswert = (e1 * w1) + (e2 * w2) + (e3 * w3) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-f60959787280ea4a182f43fca6912b3b_l3.png "Rendered by QuickLaTeX.com")
In unserem Beispiel würde sich also ergeben:
Erwartungswert für a1: (400 x 0,2) + (100 x 0,5) + (-50 x 0,3) = 115Erwartungswert für a2: (200 x 0,2) + (200 x 0,5) + (50 x 0,3) = 155Erwartungswert für a3: (100 x 0,2) + (100 x 0,5) + (100 x 0,3) = 100
Der Bratwurst-Stand-Betreiber entscheidet sich also dafür, 100 Bratwürste einzukaufen.
Das Bernoulli-Prinzip
Beim Bernoulli-Prinzip erfolgt das Treffen einer Entscheidung bei Risiko in zwei Schritten.
Im ersten Schritt wird eine individuelle Nutzenfunktion aufgestellt. Der individuelle Nutzen eines Ergebnisses einer Handlungsalternative (a) wird als U(ea) dargestellt.
Das Bernoulli-Prinzip, auch Erwartungswertnutzentheorie genannt, nimmt für den Präferenzwert des Entscheiders die Summe aus den Produkten von Eintrittswahrscheinlichkeit und Nutzenwert an. Nach dieser Entscheidungsregel entscheidet sich der Entscheidungsträger für die Alternative, die den höchsten Wert aufweist.
In unserem Beispiel nehmen wir folgende Nutzenfunktion an:
![\[ U(e) = \sqrt{e} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-ad993c8c81c9d73cbed9c5d528d7d9dd_l3.png "Rendered by QuickLaTeX.com")
Die Erwartungswerte der einzelne Handlungsalternativen sehen also folgendermaßen aus:
![\[ Erwartungswert~f\ddot{u}r~a1 : (\sqrt{400} * 0,2) + (\sqrt{100} * 0,5) + (\sqrt{-50} * 0,3) = 6,88 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-119f2d67a6b8e788e4e84c6584555c13_l3.png "Rendered by QuickLaTeX.com")
![\[ Erwartungswert~f\ddot{u}r~a2 : (\sqrt{200} * 0,2) + (\sqrt{200} * 0,5) + (\sqrt{50} * 0,3) = 12,02 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-702ea4e362a72086ece3a948c20a4210_l3.png "Rendered by QuickLaTeX.com")
![\[ Erwartungswert~f\ddot{u}r~a3 : (\sqrt{100} * 0,2) + (\sqrt{100} * 0,5) + (\sqrt{100} * 0,3) = 10 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-c7f678447bf753b2c5c2f281334ed5de_l3.png "Rendered by QuickLaTeX.com")
Nach dem Bernoulli-Prinzip und der angenommenen Nutzenfunktion würde sich der Betreiber des Bratwurststandes ebenfalls dafür entscheiden, 100 Bratwürste einzukaufen.
Vorteile und Nachteile des Modells der Entscheidung bei Risiko
- Risikobehaftete Entscheidungen können auf Grundlage der genannten Entscheidungsregeln getroffen werden.
- Nahezu jede Entscheidung in der unternehmerischen Praxis ist mit einem Risiko behaftet.
- In der Praxis können die angenommenen Eintrittswahrscheinlichkeiten nur in den seltensten Fällen mit Sicherheit vorausgesagt werden.
- Dadurch, dass auch das Eintreten anderer Umweltzustände möglich ist, kann sich die getroffene Entscheidung im Nachhinein als nicht optimal erweisen.
Übungsaufgaben
#1. Was versteht man unter Entscheidungen bei Risiko?
#2. Welche Entscheidungsregeln können angewandt werden, um Entscheidungen bei Risiko zu treffen?
#3. “Die Bayes-Regel berücksichtigt die individuelle Risiko-Affinität des Entscheidungsträgers.” – Diese Aussage ist:
#4. “Die Eintrittswahrscheinlichkeiten der einzelnen Umweltzustände spielen bei Entscheidungen unter Risiko keine Rolle” – Diese Aussage ist:
#5. “Beim Bernoulli-Prinzip wird die Variante ausgewählt, die den höchsten Erwartungsnutzenwert aufweist” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
