Bei der Indifferenzkurve geht es um eine mikroökonomische Darstellung als Bestandteil der Haushaltstheorie. Mithilfe der Indifferenzkurve erfolgt die Darstellung mehrerer Kombinationen von Gütern, die allesamt denselben Nutzen für einen Konsumenten bringen. Dieser Ansatz basiert auf der Annahme, dass es den Konsumenten schlichtweg egal ist, mit welchem Gut der Bedarf im konkreten Fall gedeckt ist.
In der folgenden Lektion geht es um die Indifferenzkurve und ihre Anwendung. Zudem gibt es im Anschluss noch einige Übungsaufgaben, mit denen du das gelernte Wissen vertiefen kannst.
- Synonyme: Iso-Nutzenkurve | Iso-Nutzenfunktion
- Englisch: indifference curve
Warum ist die Indifferenzkurve wichtig?
Die Indifferenzkurve dient dazu, die Präferenzen der Nutzer und die Möglichkeit der Bedürfnisbefriedigung widerzuspiegeln. Unternehmen und Wirtschaftswissenschaftler können mithilfe der Indifferenzkurve ermitteln, auf welche Art und Weise die Erfüllung der Bedürfnisse möglich ist.
Notwendigkeit der Indifferenzkurve
Konsumenten besitzen unterschiedliche Präferenzen. Für die Verbraucher ist es möglich, aus unterschiedlichen Kombinationen von Gütern das Passende auszuwählen. In der mikroökonomischen Theorie gilt die Prämisse, dass die Konsumenten das Bündel an Gütern wählen, welches den höchsten Nutzen bringt.
Die Konsumenten orientieren ihre Wahl am eigenen Nutzen. Falls zwei Optionen den gleichen Nutzen bringen, ist die Wahl des Konsumenten gleichgültig oder auch indifferent. Hieraus ergibt sich die Notwendigkeit der Indifferenzkurve.
Was ist die Indifferenzkurve?
Bei der Indifferenzkurve handelt es sich um eine graphische Kurve, die alle Güterbündel angibt, welche den gleichen Nutzen für den Konsumenten stiften. Es werden somit alle indifferenten Optionen zur Befriedigung der eigenen Bedürfnisse dargestellt.
Axiome der Indifferenzkurve
Die Darstellung der Präferenzen einer Kurve basieren auf unterschiedlichen Axiomen.
Bei der Indifferenzkurve basiert die Darstellung auf den beiden folgenden Axiomen:
- Vollständigkeitsaxiom
- Transitivitätsaxiom
Grafische Darstellung
Die Darstellung der Indifferenzkurve erfolgt als Graph in einem Koordinatensystem. Auf der x-Achse befindet sich die Menge des Konsums des einen Guts und auf der vertikalen Achse die Menge des anderen Produkts.
Es geht somit immer um einen Zwei-Güter-Fall. Es gibt dann unendlich viele Güter-Kombinationen, welche der Konsument wählen kann. Sämtliche Kombinationen sind für den Konsumenten gleich sinnvoll. Durch die Verbindung all dieser Kombinationen ergibt sich die Indifferenzkurve.
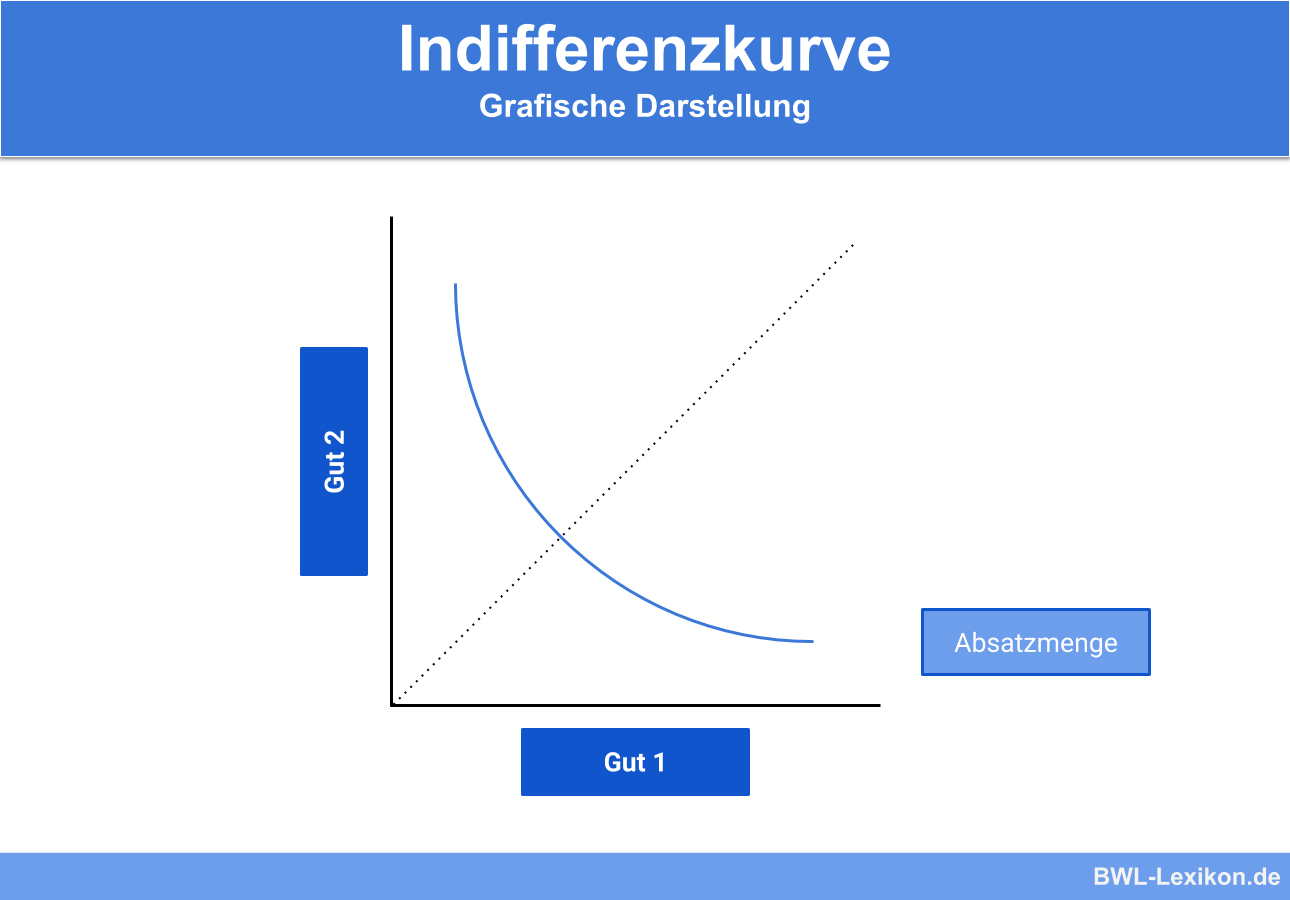
Eigenschaften der Indifferenzkurve
Die Indifferenzkurve weist unterschiedliche Eigenschaften auf, die allesamt die individuelle Präferenz der Konsumenten widerspiegeln:
- Höher liegende Indifferenzkurven werden bevorzugt
- Indifferenzkurven haben ein negatives Gefälle
- Indifferenzkurven verlaufen konvex
- Indifferenzkurven schneiden sich nicht
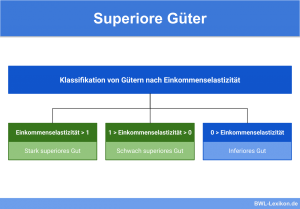
Die unterschiedlichen Nutzenfunktionen
In der Wirtschaftswissenschaft gibt es drei unterschiedliche Nutzenfunktionen, bei denen es allesamt dazugehörige Indifferenzkurven gibt.
Dabei handelt es sich um die drei folgenden Varianten:
- Perfekte Substitute
- Perfekte Komplemente
- Imperfekte Substitute
Perfekte Substitute
Bei den perfekten Substituten handelt es sich um eine Nutzenfunktion, bei der sämtliche Güter beliebig austauschbar sind. Der Nutzen ist für den Konsumenten genau gleich.
Formel:
![\[ u(x_1,x_2) = (a*x_1) + (b*x_2) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-f14d4f2ccd715fdadf4ccf005c2e4d25_l3.png "Rendered by QuickLaTeX.com")
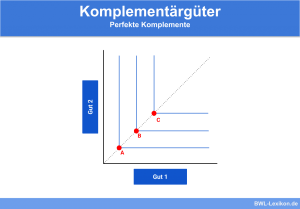
Perfekte Komplemente
Bei den perfekten Komplementen handelt es sich um Güter, die sich gegenseitig vervollständigen. Die Konsumenten benötigen beide Güter. Nur ein Gut alleine kann dem Verbraucher keinen Nutzen bringen. Somit handelt es sich bei der Formel um eine Minimum-Funktion, da jedes Komplement das passende Gegenstück braucht, um einen Nutzen zu generieren.
Formel:
![\[ u(x_1,x_2) = min\{ax_1,bx_2\} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-cd0b955037a2d76826a3bcf5d6e8e703_l3.png "Rendered by QuickLaTeX.com")
Imperfekte Substitute
Die Imperfekten Substitute bilden eine weitere Nutzenfunktion ab. Bei den Imperfekten Substituten handelt es sich um Güter, die einen ähnlichen Nutzen bringen, denen jedoch Unterschiede inhärent sind.
Beispielsweise unterscheiden sich die Güter hinsichtlich Preis oder Qualität. Bei den Imperfekten Substituten ist die “Cobb-Douglas-Funktion” die gängigste Variante.
Formel:
![\[ u(x_1,x_2) = (x_1^{\alpha}) * (x_2^{\beta}) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-546d0b760c029f13ef3c22a68cb3ddb3_l3.png "Rendered by QuickLaTeX.com")
Übungsfragen
#1. Was bildet die Indifferenzkurve ab?
#2. Welche Eigenschaft trifft auf Indifferenzkurven zu?
#3. Was ist ein Synonym für die Indifferenzkurve?
#4. Die Indifferenzkurve hat niemals eine negative Steigung.
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
