Isoquante

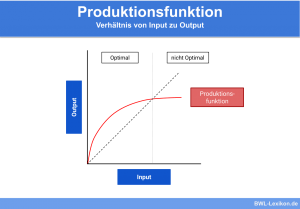
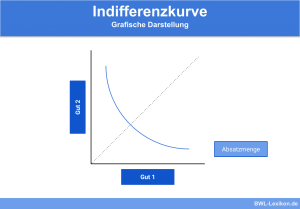
Die Isoquante ist ein Begriff aus der Produktionsfunktion. Es handelt sich um ein geometrisches Konstrukt, welches in einem Achsendiagramm eingezeichnet wird. Unternehmen können der Isoquante entnehmen, welche Menge an Produktionsfaktoren sie benötigen, um eine vorgegebene Menge an Output zu erreichen. Im Normalfall werden zwei Produktionsfaktoren verglichen, die substitutional zueinander sind, sich also austauschen lassen. Es existieren jedoch verschiedene andere Formen, die eine Isoquante im Normalfall einnehmen kann.

In dieser Lektion lernst du den Begriff der Isoquante kennen. Du erhältst einen Überblick darüber, wie die Isoquante berechnet und gezeichnet wird. Außerdem stellen wir dir die drei gängigen Verläufe einer Isoquante vor. Die Lektion schließt mit einigen Übungsaufgaben ab.

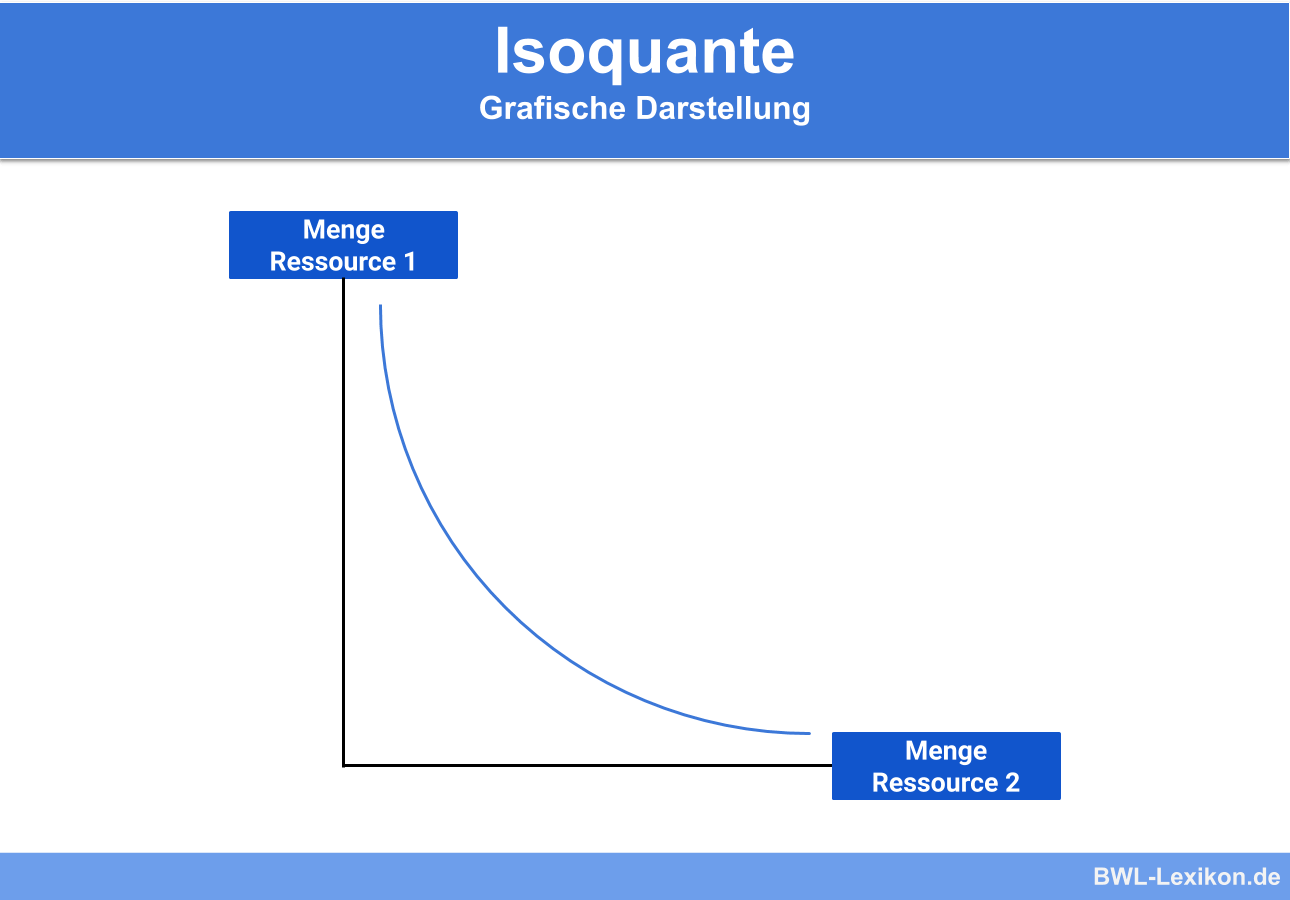
Was ist die Isoquante?

Unternehmen nutzen die Isoquante, um hierüber den benötigten Input für eine zuvor bestimmte Menge Output zu erkennen. Die Isoquante ist eine grafische Darstellung, die aus einer Produktionsfunktion bestimmt wird.

Aus sich ergebenden Faktorkombinationen kann der Wert der Ausbringungsmenge abgelesen werden. Die Ausbringungsmenge bleibt somit stetig gleich und die Produktionsfaktoren lassen sich austauschen, bzw. ergänzen sich.

In der Praxis kann ein Unternehmen somit entscheiden, welche Produktionsmethoden es für eine gewünschte Leistung nutzen kann. Die Entscheidung erfolgt letztendlich über das Produktionsziel, welches sich beispielsweise in Kosten oder in der Herstellzeit ausdrücken kann. Das Wort Isoquante setzt sich aus iso=gleich und quant=Menge zusammen, womit die immer gleiche Menge vom Output gemeint ist.

Isoquante berechnen und zeichnen

Die Formel der Isoquante ist das Verhältnis vom Output zu mehreren Produktionsfaktoren. Sie lautet:

Y wird vom Unternehmen bestimmt, während x1 und folgende die jeweiligen Produktionsfaktoren darstellen. Hieraus entstehen zahlreiche Möglichkeiten, wie ein Unternehmen zu Y gelangen kann. Das Ergebnis lässt sich grafisch darstellen.

Im einfachen Fall wird von zwei Produktionsfaktoren ausgegangen. Ein Faktor ist auf der X-Achse und ein Faktor auf der Y-Achse abzulesen. Aus der eingezeichneten Isoquante lässt sich nun ablesen, welche weiteren Produktionsfaktoren benötigt werden, wenn bereits einer der beiden Faktoren bekannt ist.

Das Unternehmen benötigt 25 Mengeneinheiten Schafwolle, damit gemeinsam mit den restlichen 30 Mengeneinheiten Baumwolle die geforderten 40 Schlafanzüge produziert werden können.

Steigung der Isoquante

Die Isoquante steigt über die Menge der Produktionsfaktoren an. Dabei bestehen verschiedene Möglichkeiten der Steigung. Stehen die Produktionsfaktoren beispielsweise in einem linearen Verhältnis, handelt es sich bei der Isoquante um einen gleichmäßig ansteigenden Graphen. Aber auch eine negative Steigung oder überproportionale Steigungen sind möglich.

Gängige Isoquanten:

• Perfekte Substitute
• Perfekte Komplemente
• Imperfekte Substitute

Perfekte Substitute

Bei perfekten Substituten sind die Produktionsfaktoren beliebig miteinander kombinier- und austauschbar. Beispielhaft lassen sich hier Substitutionsgüter wie Diesel und Erdgas, Baumwolle und Schafwolle oder Butter und Margarine nennen.

Das Ergebnis der perfekten Substitute ist eine gerade Linie der Isoquanten. Dies hat den Vorteil, dass immer die gewünschte Outputmenge erreicht wird und das benötigte Material dennoch beliebig ausgetauscht werden kann. Das Unternehmen kann also das Material verwenden, welches am günstigsten ist, welches gerade ablaufen wird oder welches der Kunde vorschreibt. Eine freie Auswahl ist möglich.

Perfekte Komplemente

Bei perfekten Komplementen werden zwei Produktionsfaktoren benötigt, die in einem gewissen Verhältnis zueinander stehen.

Dieses Mischungsverhältnis kann nicht verändert werden, sodass die Austauschbarkeit fehlt. Hier greift die Minimum-Funktion. Diese besagt, dass immer nur so viel Output entstehen kann, wie vom Produkt mit der kleinsten Menge vorhanden ist. Dies lässt sich am ehesten in einem Beispiel darstellen.

Imperfekte Substitute

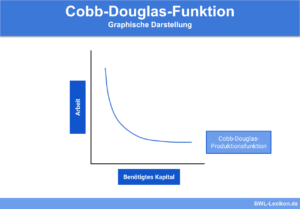
Die imperfekten Substitute bedarfen eine deutlich komplexeren Formel, bei der die Produktionsfaktoren sich in ihrer Qualität unterscheiden und somit nicht wahllos ersetzen lassen. Von den imperfekten Substituten existieren verschiedene Formen, wobei die Cobb-Douglas-Produktionsfunktion überwiegend eingesetzt wird.

Das Aussehen dieser Isoquante ist eine Exponentialfunktion, die sich konvex darstellt. Das bedeutet, dass ein Produktionsfaktor mehr Gewicht findet als ein anderer.

Übungsfragen