Produktionsfunktion

Die Produktionsfunktion ist eine mathematische Formel zur Berechnung von Ausbringungsmengen, wenn die Einsatzmengen bekannt sind. Es können also aus den Produktionsfaktoren Kapital und Arbeit die daraus produzierten Güter und Dienstleistungen errechnet werden. Es wird zwischen substitutionalen und limitationalen Produktionsfunktionen unterschieden.

Diese Lektion erklärt dir die Produktionsfunktion und gibt Auskunft darüber, wie deren Berechnung erfolgt. Du erhältst außerdem eine Übersicht der verschiedenen Ausprägungen der Funktion. Den Abschluss der Lektion bilden einige Übungsaufgaben.

Warum ist die Produktionsfunktion wichtig?

Unternehmen haben über die Produktionsfunktion die Möglichkeit, ihren Output zu berechnen und zu optimieren. Hierdurch können Aufträge kalkuliert und Auskünfte gegenüber Kunden gemacht werden.

Durch die unterschiedlichen Arten der Produktionsfunktion können Unternehmen die benötigten Produktionsfaktoren für eine bestimmte Menge an Produkten errechnen oder aus bestimmten Produktionsfaktoren die produzierte Menge bestimmen.

Aufbau der Produktionsfunktion (Formel)

Mit der Produktionsfunktion wird der Output mit den vorhandenen Produktionsfaktoren Kapital und Arbeit in Zusammenhang gesetzt.

Ein Unternehmen hat über die Funktion die Möglichkeit, seine maximale Produktion zu errechnen. Es kann feststellen, wie viele Produkte oder Dienstleistungen es aus gegebenen Produktionsfaktoren herstellen kann. Eine zweite Rechenmethode erklärt einem Unternehmen, welche Produktionsfaktoren es einsetzen muss, damit eine zuvor bestimmte Menge an Produkten hergestellt werden kann.

Grafische Darstellung

Die Funktion lässt sich auch immer grafisch darstellen.

Auf der x-Achse wird das eingesetzte Kapital und auf der y-Achse die Menge der produzierten Artikel oder der erbrachten Dienstleistungen eingetragen.

Die Formel lautet:

In diesem Fall ist f(x) die erzeugte Menge an Produkten. X stellt die eingesetzte Menge Kapital dar und y ist die Menge, die eine Einheit vom eingesetzten Kapital im betrachteten Zeitraum herstellt.

Es handelt sich um eine sehr einfache Funktion, bei der keine weiteren Gegebenheiten beachtet werden. Die grafische Darstellung dieser Funktion ist eine linear ansteigende Linie.

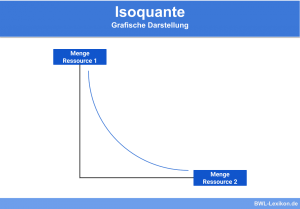
Substitutionale Produktionsfunktion

Die substitutionale Produktionsfunktion gibt einem Unternehmen Aufschluss darüber, wie es seine Produktionsfaktoren austauschen kann, um letztendlich die gleiche Menge an Output zu erreichen.

Beispielsweise lässt sich prüfen, wie viele Maschinen benötigt werden, um die Arbeitskraft „Mensch“ in der Produktion zu ersetzen. Die totale Substitutionalität beschreibt eine Funktion, bei der ein Faktor komplett durch einen anderen Faktor ersetzt werden kann.

Bei der peripheren Substitutionalität ist dies nur begrenzt möglich. Es bestehen verschiedene Formen der substitutionalen Produktionsfunktion, die jeweils eine hohe Komplexität besitzen und im Gegensatz zur einfachen Funktion weitere Begleitumstände beachten.

Mögliche substitutionale Produktionsfunktionen:

• Ertragsgesetzliche Produktionsfunktion (Typ A)
• Cobb Douglas Produktionsfunktion
• CES-Funktion

Ertragsgesetzliche Produktionsfunktion (Typ A)

Die ertragsgesetzliche Produktionsfunktion, auch als Typ A bezeichnet, ist eine Funktion, bei der sich zwei Inputfaktoren auf den Output auswirken. Einer der Faktoren ist konstant und der zweite Faktor kann angepasst werden. Bei dieser speziellen Form steigt der Output bei einer gesteigerten Menge des variablen Faktors deutlich. Wird dieser Faktor jedoch weiter gesteigert, steigt die Menge vom Output nicht mehr mit, sondern flacht ab und fällt.

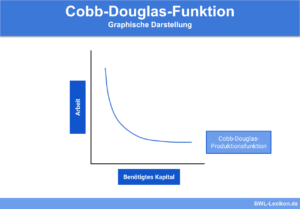
Cobb Douglas Produktionsfunktion

Eine weitere substitutionale Funktion, die von Charles Cobb und Paul Douglas entwickelt wurde, besitzt die Besonderheit, dass kein Maximum in der Outputmenge erreicht werden kann.

Hierbei wird im Gegensatz zur ertragsgesetzlichen Produktionsfunktion angenommen, dass veränderte Inputmengen die Produktion dauerhaft ansteigen lassen. Dies geschieht aber nicht stetig steigend, wie bei der einfachen Produktionsfunktion. Bei der Cobb Douglas Funktion flacht der Anstieg immer mehr ab, bis er zu einer Stagnation tendiert.

Limitationale Produktionsfunktion

Limitationale Produktionsfunktionen geben einem Unternehmen Auskunft über den Output. Die Produktionsfaktoren sind nicht beliebig austauschbar, sondern es muss für eine Steigerung des Outputs auch immer eine passende Steigung der Produktionsfaktoren vorhanden sein. Insbesondere bei zwei oder mehr Produktionsfaktoren muss beachtet werden, dass der Input in einem passenden Verhältnis gesteigert wird, damit auch der Output steigen kann.

Die limitationalen Produktionsfunktionen geben die optimale Menge vom Input aus, sodass der Output gleichmäßig steigen kann. Es werden Verschwendungen vom Input vermieden. Die limitationalen Produktionsfunktionen werden in die lineare und nichtlineare Funktion unterteilt.

Linear-limitationale Produktionsfunktion

Bei der linear-limitationalen Produktionsfunktion stehen die Produktionsfaktoren in einem festen Verhältnis und sorgen nur für mehr Output, wenn das passende Verhältnis eingehalten wird.

Die Funktion gibt Aufschluss darüber, wie die Produktionsfaktoren in einem passenden Verhältnis gesteigert werden müssen und wie groß der Output der jeweiligen Funktion sein wird. Eine Form der linear-limitationalen Produktionsfunktion ist die Leontief-Produktionsfunktion.

Nichtlinear-limitationale Produktionsfunktion

Bei den nichtlinearen limitationalen Produktionsfunktionen ist das Verhältnis im Gegensatz zu den linearen Funktionen nicht konstant. Hieraus ergeben sich komplexe Formeln, die bei mehreren Einflussfaktoren den Output wiedergeben können.

Diese Formel wird häufig bei Produktionsanlagen verwendet. Hier spielen die Maschinen und deren Geschwindigkeit, die Kapazitäten und viele weitere Faktoren eine wichtige Rolle. Ein Beispiel für die nichtlineare limitationale Produktionsfunktion ist die Gutenberg-Produktionsfunktion.

Übungsfragen