▷ Cobb Douglas Funktion » Definition, Erklärung & Beispiele + Übungsfragen

In der Mikroökonomie stellt die Cobb-Douglas-Funktion stellt die Auswirkungen von Arbeit und Kapital auf den gewünschten Output dar. Sie kann aber auch als Nutzenfunktion angewendet werden.

Dieses Kapitel wird dir zeigen, was genau die Cobb-Douglas-Funktion ist und welche Bedeutung sie hat. Wir zeigen dir auch, wie du diese anwenden kannst. Im Anschluss kannst du mit unseren Übungsaufgaben dein Wissen zu Cobb-Douglas-Funktion überprüfen.

Synonym: Cobb-Douglas-Produktionsfunktion
Englisch: Cobb–Douglas production function

Welche Bedeutung hat die Cobb-Douglas-Funktion?

Die Cobb-Douglas-Funktion kann sowohl als Produktions- als auch als Nutzenfunktion genutzt werden. In der Verwendung als Produktionsfunktion kann die Cobb-Douglas-Funktion genutzt werden, um die Änderung des Outputs durch Veränderungen der Faktoren Arbeit und Kapital zu berechnen. Natürlich funktioniert auch die umgekehrte Anwendung, mit der herausgefunden werden kann, wie sich die beiden Faktoren ändern müssen, um einen bestimmten gewünschten Output zu erreichen.

Als Nutzenfunktion angewendet beschreibt die Cobb-Douglas-Funktion die Veränderung (Erhöhung oder Verminderung) des Nutzens durch die Erhöhung oder Verminderung des Konsums eines oder mehrerer Güter.

Was versteht man unter der Cobb-Douglas-Funktion?

Die Cobb-Douglas-Funktion wird in der Volkswirtschaftslehre, genauer in der Mikroökonomie genutzt, um die Zusammenhänge der zwei Faktoren Arbeit und Kapital und deren Auswirkung auf den zu erwartenden Output darzustellen. Die beiden Faktoren sind dabei substitutional, also austauschbar.

In der Grundform sieht die Cobb-Douglas-Funktion folgendermaßen aus:

$Y = a * L^\alpha * K^\beta$

Die einzelnen Bestandteile stehen für:

Y = Menge des Outputs
K = Einsatz des Faktors Kapital
L = Einsatz des Faktors Arbeit
α = Produktionselastizität des Outputs in Abhängigkeit zum Faktor Arbeit
β = Produktionselastizität des Outputs in Abhängigkeit zum Faktor Kapital
a = Effizienzparameter

Anhand der Parameter der Produktionselastizität und können Rückschlüsse auf die Art der Skalierung gezogen werden.

So bedeutet:

+1, dass es sich um abnehmende Skalenerträge handelt
+=1, dass es sich um konstante Skalenerträge handelt
+>1, dass es sich um zunehmende Skalenerträge handelt

Bei konstanten Skalenerträgen führt die Verdopplung der Menge je Produktionsfaktor zu einer Verdopplung der gesamten Menge des Outputs.

Die Cobb-Douglas-Funktion kann in diesem Fall auch in folgender Form geschrieben werden:

$Y = a * L^\alpha * K^{1-\alpha}$

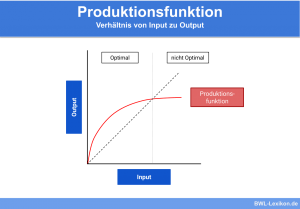
Die Cobb-Douglas-Funktion als Produktionsfunktion

Um die Verwendung der Cobb-Douglas-Funktion als Produktionsfunktion zu erläutern, nehmen wir folgendes Beispiel an:

Es sei die Produktionsfunktion

$Y = a * L^{0,7} * K^{0,3}$

gegeben, wobei der Output konstant auf einem Niveau von 20 liegt. Es soll nun also für eine konstante Produktionsmenge die Verteilung der Faktoren bestimmt werden. Hierfür werden die Parameter entsprechend eingesetzt, um den jeweils anderen Faktor zu bestimmen.

Beispiel

Nehmen wir an, die “Cobby AG”, tätig in der Herstellung von Sitzmöbeln, möchte pro Schicht 20 Stühle produzieren (= Output). Nun soll bestimmt werden, wie sich die einzelnen Faktoren verhalten. Es wird angenommen, dass in einer Schicht 20 Mitarbeiter (= Faktor Arbeit) arbeiten.

Diese setzt man nun in die gegebene Produktionsfunktion ein:

$20 = 1 * 20^{0,7} * K^{0,3}$

Durch Umstellung der Produktionsfunktion kann nun das benötigte Kapital berechnet werden. Auch weitere Varianten können durchgespielt werden, beispielsweise wie sich der Kapitalbedarf ändert, wenn 30 Mitarbeiter in einer Schicht arbeiten.

Neben der rechnerischen Lösung ist auch eine graphische Lösung möglich, indem die Produktionsfunktion in einem Koordinatensystem dargestellt wird:

Die Cobb-Douglas-Funktion als Nutzenfunktion

Neben der Anwendung als Produktionsfunktion kann die Cobb-Douglas-Funktion auch als Nutzenfunktion verwendet werden. Hierbei wird die Grenzrate und der Grenznutzen der Substitution zur Berechnung der Maximierung des Nutzens verwendet.

In dieser Form der Anwendung sieht die Cobb-Douglas-Funktion wie folgt aus:

$U(x_1,x_2) = x^a_1 * x^{1-\alpha}_2$

Die einzelnen Parameter stehen in diesem Fall für:

U = Nutzen
x₁= Wirtschaftsgut 1
x₂= Wirtschaftsgut 2
α = Präferenz des Individuums

In dieser Form der Anwendung kann die Cobb-Douglas-Funktion genutzt werden, um die Auswirkungen auf den Nutzen des Individuums durch die Veränderung der Konsummenge eines der beiden betrachteten Wirtschaftsgüter in Abhängigkeit der individuellen Präferenzen zu analysieren. So kann herausgefunden werden, welches der betrachteten Güter vom Individuum bevorzugt wird.

Beispiel

Lieselotte hat von Ihrer Oma 10 Euro Taschengeld bekommen, um sich selbst eine Freude zu machen. Mit diesen 10 Euro geht sie zum Kiosk um die Ecke, um sich Süßigkeiten zu kaufen. Am liebsten mag Sie Bonbons (x₁) und Lollies (x₂).

Ein Bonbon kostet 75 Cent.
Ein Lollie kostet 1 Euro.

Lieselotte kann sich nicht recht entscheiden, was sie kaufen soll. Da sie ein schlaues Mädchen ist, nutzt Sie die Cobb-Douglas-Nutzenfunktion, um herauszufinden, wie sie ihren Nutzen maximieren kann.

Sie stellt dazu folgende Funktion auf:

$U(x_1,x_2) = x^{0,5}_1 * x^{0,5}_2$

Wenn Lieselotte nur einen Lollie kauft, kann Sie sich noch 12 Bonbons leisten, um das Budget voll auszunutzen.

Ihr Nutzen beträgt dann:

$U(x_1,x_2) = 12^{0,5} * 1^{0,5} = 3.4641016151377544$

Durch ersetzen der Menge von x1und x2unter Berücksichtigung des vorhanden Budgets kann Lieselotte ermitteln, wie sie Ihren Nutzen maximieren kann.

Cobb Douglas Funktion

Welche Bedeutung hat die Cobb-Douglas-Funktion?

Was versteht man unter der Cobb-Douglas-Funktion?

Die Cobb-Douglas-Funktion als Produktionsfunktion

Die Cobb-Douglas-Funktion als Nutzenfunktion

Übungsfragen

#1. Was versteht man unter der Cobb-Douglas-Funktion?

#2. Wozu kann die Cobb-Douglas-Funktion genutzt werden?

#3. “Bei konstanten Skalenerträgen führt eine Verdopplung der einzelnen Produktionsfaktoren automatisch zur Verdopplung der Outputmenge.” — Diese Aussage ist:

#4. “Die Parameter der Produktionselastizität und beschreiben die Art der Skalierung der Cobb-Douglas-Funktion.” — Diese Aussage ist:

#5. “Die Cobb-Douglas-Funktion wird vor allem in der Makroökonomie genutzt.” — diese Aussage ist:

Ergebnis

Nichts passendes dabei?