▷ Erlösfunktion » Definition, Erklärung & Beispiele + Übungsfragen

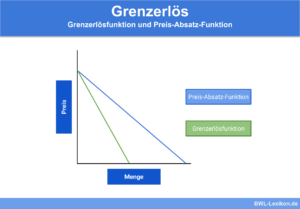
Die Erlösfunktion gibt den durch den Verkauf eines Produkts erzielten Erlös eines Unternehmens an. Sie besteht aus dem Produkt der Preis-Absatz-Funktion und der verkauften Menge.

Du wirst in diesem Kapitel nicht nur die Bedeutung der Erlösfunktion kennenlernen und was man darunter versteht. Wir zeigen dir außerdem noch, wie die Erlösfunktion berechnet wird. Ob du das nötige Wissen zur Erlösfunktion bereits gut verinnerlicht hast, kannst du im Anschluss anhand einiger Übungsaufgaben überprüfen.

Synoynme: Ertragsfunktion | Umsatzfunktion
Englisch: revenue function

Inhalt dieser Lektion

Welche Bedeutung hat die Erlösfunktion?

Durch die Fertigung und den Verkauf von Produkten oder das Anbieten von Dienstleistungen möchten Unternehmen Erlöse erzielen. Diese sollten im besten Fall die Kosten des Unternehmens übersteigen, damit ein Gewinn erzielt werden kann. Ohne Verkaufserlöse ist ein Unternehmen wirtschaftlich nicht überlebensfähig.

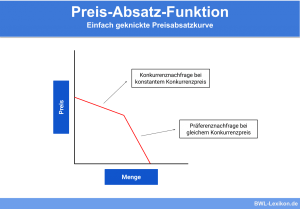
Welche Erlöse erzielt werden können, kann mit der Erlösfunktion in Erfahrung gebracht werden. Sofern die Preis-Absatz-Funktion bekannt ist, kann anhand der Erlösfunktion der zu erzielende Erlös berechnet werden.

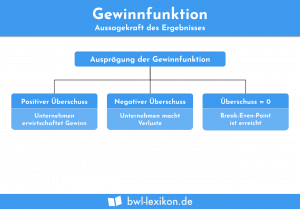
Die Erlösfunktion ist außerdem ein wichtiger Bestandteil der Gewinnfunktion (G(x)). Innerhalb der Gewinnfunktion muss die Kostenfunktion (K(x)) von der Erlösfunktion abgezogen werden, um den realisierten Gewinn bei einer bestimmten Absatzmenge (x) zu ermitteln.

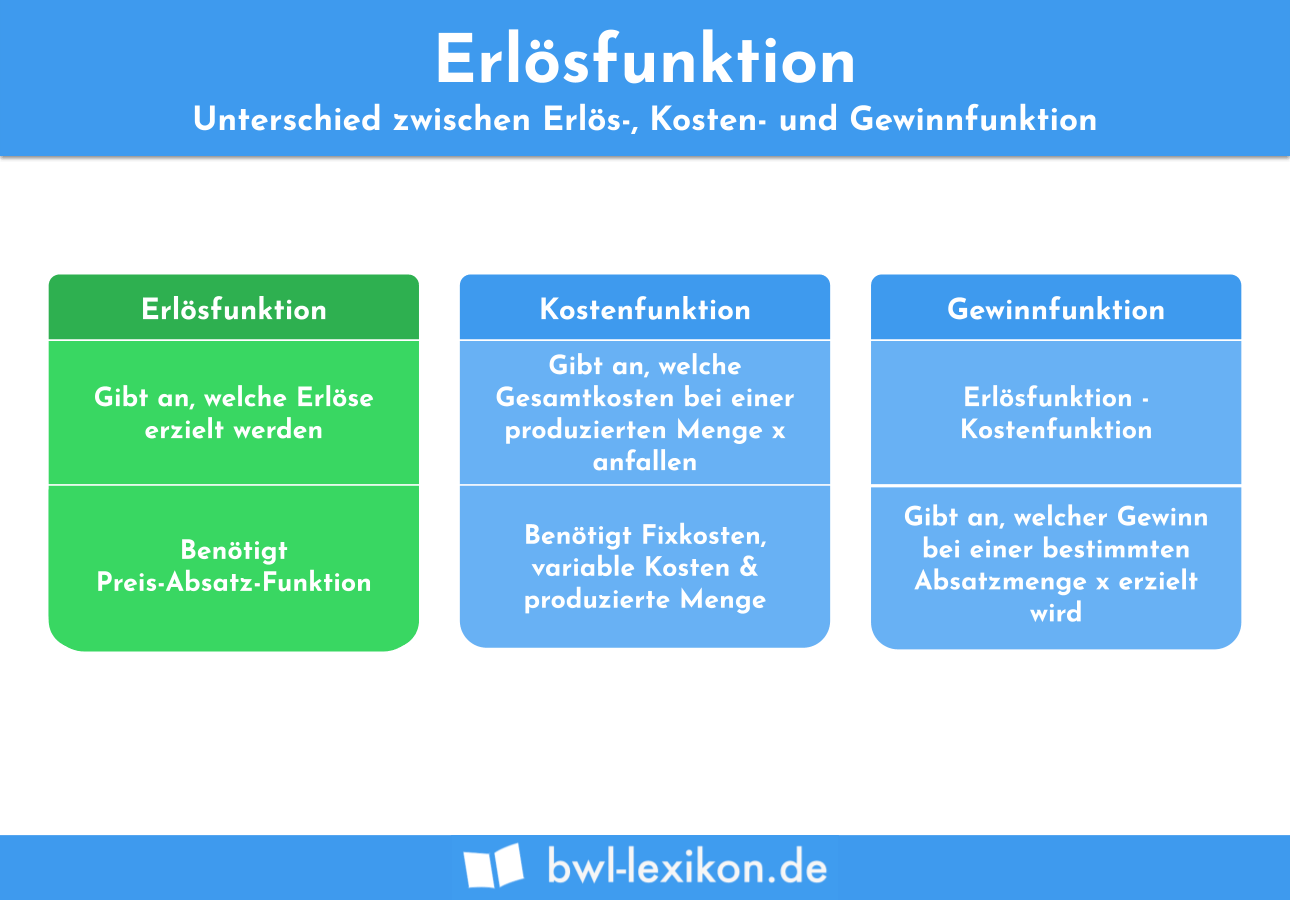
Erlösfunktion: Unterschied zwischen Erlös-, Kosten- und Gewinnfunktion

Was ist die Erlösfunktion?

Anhand der Erlösfunktion kann der Umsatz bzw. Erlös ermittelt werden, welcher durch den Verkauf eines Produkts erzielt wird. Gebildet wird die Erlösfunktion (E(x)), indem die Preis-Absatz-Funktion (p(x)) mit der Absatzmenge (x) multipliziert wird:

$E(x) = p(x) * x$

Beispiel zur Erlösfunktion

Die ”Erdapfelstäbchen AG” stellt Tiefkühlpommes her und vertreibt diese. Eine neue Pommessorte mit Zimtgeschmack soll passend zur Weihnachtszeit als saisonales Produkt auf den Markt gebracht werden. Im Monat Dezember wird mit einem Absatz von 1.000 Tüten Tiefkühlpommes gerechnet. Die Geschäftsleitung möchte nun von dir wissen, welche Erlöse dadurch erzielt werden können.

Gegeben sei die Preis-Absatzfunktion:

$p(x) = -0,5x + 1.000$

Um die Erlösfunktion (E(x)) aufstellen zu können, muss die Preis-Absatz-Funktion (p(x)) nun mit der Absatzmenge (x) multipliziert werden:

$E(x) = (-0,5x + 1.000) * x$

$E(x) = 0,5x^{2} * 1.000x$

Nachdem die Erlösfunktion aufgestellt ist, kann die geplante Absatzmenge von 1.000 Pommestüten nun in die Erlösfunktion eingesetzt werden:

$E(x) = 0,5 * 1.000^{2} + 1.000 * 1.000$

$E(x) = 500.000$

Sofern die geplante Absatzmenge von 1.000 Pommestüten erreicht werden kann, erzielt das Unternehmen einen Erlös von 500.000 Euro. Um den dadurch entsprechend erwirtschafteten Gewinn zu errechnen, müsste nun noch die Kostenfunktion abgezogen werden.