▷ Kostenfunktion » Definition, Erklärung & Beispiele + Übungsfragen

Eine Kostenfunktion dient der Darstellung des Zusammenhangs zwischen der produzierten Menge und den sich daraus ergebenden Gesamtkosten. Unterschieden werden kann zwischen linearer, progressiver, degressiver und regressiver Kostenfunktion.

Du erfährst in diesem Kapitel, was eine Kostenfunktion ist, was sie ausmacht und wofür sie benötigt wird. Um dein erlerntes Wissen zu überprüfen, haben wir dir am Ende des Kapitels einige Übungsaufgaben bereitgestellt.

Synonyme: Gesamtkostenfunktion | Totalkostenfunktion

Inhalt dieser Lektion

Welche Bedeutung hat die Kostenfunktion?

Anhand der Kostenfunktion können der Zusammenhang und die Entwicklung der Gesamtkosten in Abhängigkeit der produzierten Menge in einem Unternehmen dargestellt und untersucht werden. Sie kann damit unter anderem der Ermittlung der optimalen Produktionsmenge sowie der Kostenplanung im Zusammenhang mit der Produktionsplanung dienen. So lässt sich beispielsweise ermitteln, ob sich die Gesamtkosten eines Unternehmens bei Erhöhung der Produktionsmenge linear, degressiv oder progressiv verändern. Außerdem lassen sich anhand der Kostenfunktion die Durchschnittskosten sowie die Grenzkosten ermitteln.

Was versteht man unter der Kostenfunktion?

Anhand der Kostenfunktion können die Gesamtkosten (K(x)) eines Unternehmens angegeben werden, die anfallen, wenn eine bestimmte Menge x eines Gutes produziert wird.

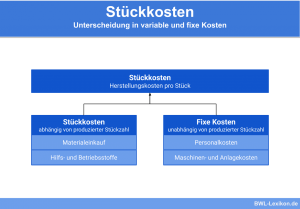
Bestandteile einer jeden Kostenfunktion sind:

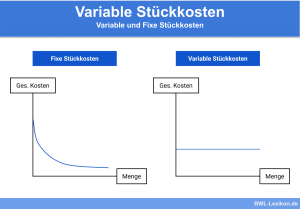
Fixkosten (K_F): Kosten, die unabhängig von der produzierten Menge x anfallen, beispielsweise für Miete, Gehälter oder Ähnliches.
variable Kosten (k_var): Kosten, die abhängig von der produzierten Menge x entstehen, beispielsweise für Rohstoffe, Energie, Betriebs- und Hilfsstoffe oder Ähnliches.
produzierte Menge x: Anzahl der produzierten Güter

Formel für die Kostenfunktion

Im Grundsatz sieht jede Kostenfunktion folgendermaßen aus:

$Gesamtkosten = Fixkosten + variable~Kosten * produzierte~Menge$

Die Kurzform lautet:

$K(x) = K_{F} + k_{var} * x$

Anhand der Formel der Kostenfunktion ist zu erkennen, dass diese der Ermittlung der Gesamtkosten des Unternehmens dient. Durch Einsetzen der entsprechenden Variablen können diese ermittelt werden.

Kostenfunktion zur Ermittlung der Grenzkosten und der Durchschnittskosten

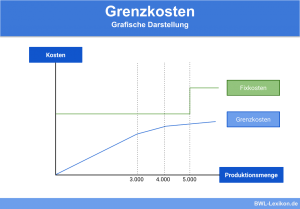
Neben der Ermittlung der Gesamtkosten können anhand der Kostenfunktion auch die Grenzkosten und die Durchschnittskosten ermittelt werden.

Grenzkosten (GK(x)): Kosten die durch die Produktion einer zusätzlichen Mengeneinheit entstehen.
Durchschnittskosten (DK(x)): fixe und variable Kosten einer produzierten Einheit.

Die Durchschnittskosten können ermittelt werden, indem die Kostenfunktion durch die produziert Menge x geteilt wird:

$DK(x) = \frac{K(x)}{x}$

Die Grenzkosten werden durch die erste Ableitung der Kostenfunktion ermittelt:

$GK(x) = K´(x)$

Die Grenzkosten, auch Marginalkosten genannt, sind interessant, da die Durchschnittskosten in den meisten Fällen bei unterschiedlichen Produktionsmengen variieren. Demnach gibt es eine Produktionsmenge, bei der die geringsten Durchschnittskosten anfallen. Diese befindet sich am Schnittpunkt von Grenz- und Durchschnittskosten.

Verschiedene Arten von Kostenfunktionen

Die am häufigsten anzutreffenden Arten von Kostenfunktionen sind:

die lineare Kostenfunktion
die degressive Kostenfunktion
die progressive Kostenfunktion

Daneben existieren auch regressive Kostenfunktionen, welche in Produktion von Betrieben aber nur an bestimmten Stellen und relativ selten vorkommen. Vor allem die Gesamtkosten eines Betrieben verhalten sich in den meisten Fällen nicht regressiv. Auch lassen sich die einzelnen Kostenarten Fixkosten und variable Kosten in einzelnen Kostenfunktionen darstellen.

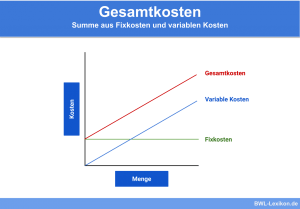
Die Entwicklung der Gesamtkosten, wie auch die der Grenz- und Durchschnittskosten, verläuft bei den einzelnen Arten der Kostenfunktion unterschiedlich. Der Verlauf der Kostenfunktion ist dabei vor allem von den variablen Kosten abhängig. Die Fixkosten bestimmen dabei lediglich den Abschnitt auf der y-Achse.

Lineare Kostenfunktion

Eine lineare Kostenfunktion liegt vor, wenn die variablen Kosten proportional zur produzierten Menge ansteigen. Mit zunehmender Produktionsmenge nehmen die Durchschnittskosten ab, da die Fixkosten auf eine immer größer werdende produzierte Menge aufgeteilt werden. Die Grenzkosten bei einer linearen Kostenfunktion sind konstant und entsprechen den variablen Durchschnittskosten.

Bei einer beispielhaften Kostenfunktion von K(x) = 3 + 0,5 x ergeben sich folgende Verläufe der Graphen:

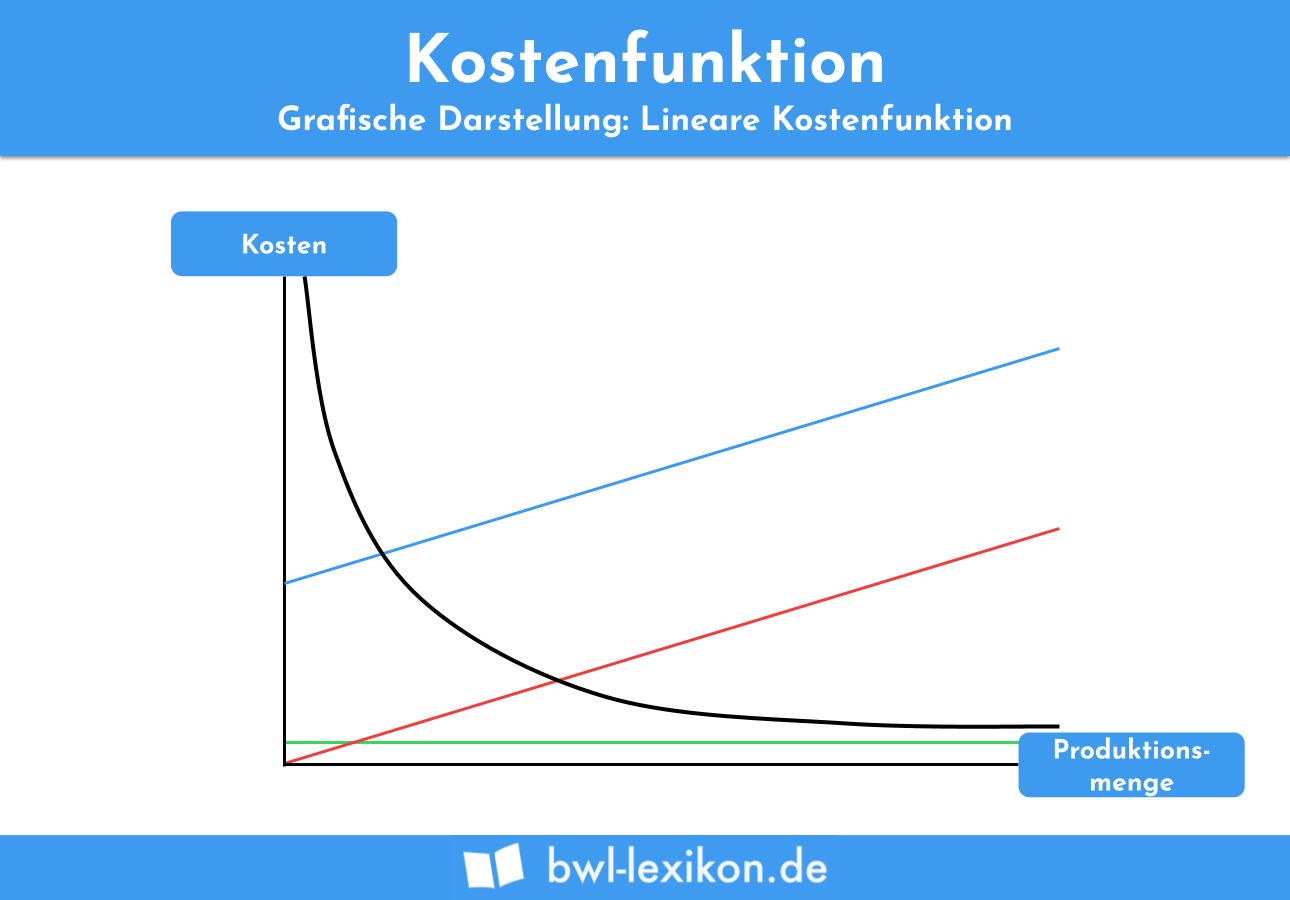
Kostenfunktion = Blau
variable Kosten = Rot
Grenzkosten / durchschnittliche variable Kosten = Grün
Durchschnittskosten = Schwarz

Beispiel: Lineare Kostenfunktion

Die Schüler Max, Paul und Amelie möchten Geld für ihre Klassenfahrt sammeln. Dafür haben sie sich überlegt, auf dem Sommerfest der Schule selbst gebackene Muffins zu verkaufen. Dazu müssen zunächst die Zutaten besorgt werden. Insgesamt geben sie dafür 100 Euro aus. Insgesamt reichen die eingekauften Zutaten für 500 Muffins. Zusätzlich kaufen sie zwei Muffin-Backformen für jeweils fünf Euro. Wie jeder Stand auf dem Schulfest müssen auch die Schüler eine Standgebühr entrichten. Die Schulleiterin kommt den Kindern entgegen und nimmt nur eine reduzierte Standgebühr in Höhe von 20 Euro. Gebacken werden die Muffins in der Küche von Pauls Oma, die den Kindern keine Energiekosten berechnet.

Max: dein kleiner Bruder, bittet dich um Hilfe bei der Erstellung der Kostenfunktion.

Um diese aufzustellen, müssen zunächst die fixen und die variablen Kosten ermittelt werden.

Ermittlung der Fixkosten:
Die nicht variablen Kosten bestehen aus der Gebühr für den Stand auf dem Schulfest und den Kosten für die beiden Backformen.
Damit ergeben sich folgende Fixkosten:

$K_{F} = 20~Euro + 10~Euro = 30~Euro$
Ermittlung der variablen Kosten:
Im Gegensatz zu den fixen Kosten sind die variablen Kosten abhängig von der produzierten Menge. In diesem Fall zählen zu den variablen Kosten also die Kosten für die Zutaten für die Muffins.
Um die variablen Kosten pro Stück zu erhalten, werden die 100 Euro für die Zutaten durch die 500 zu backenden Muffins geteilt:

$k_{var}=\frac{100~Euro}{500~Stück}=0,2~Euro~pro~Stück$

Die Produktion eines Muffins kostet also 20 Cent.

Sind die fixen und die variablen Kosten ermittelt, kann die Kostenfunktion aufgestellt werden:

$K(x) = K_{F} + k_{var} * x$

$K(x) = 30~Euro + 0,2~Euro~pro~Stück * 500~Stück$

$K(x) = 130~Euro$

Die Gesamtkosten betragen also 130 Euro.

Am Tag vor dem Sommerfest erfährt Paul, dass auch Schüler einer anderen Schule das Sommerfest besuchen möchten. Die geplanten 500 Muffins werden daher nicht ausreichen. Kurzerhand wird entschlossen, 750 Muffins zu backen.

Da die Kostenfunktion bereits erstellt ist, kann die nun neue Menge einfach in diese eingesetzt werden, um die neuen Gesamtkosten zu ermitteln:

$K(x) = 30~Euro + 0,2~Euro~pro~Stück * 750~Stück$

$K(x) = 180~Euro$

Degressive Kostenfunktion

Die degressive Kostenfunktion zeichnet sich durch eine unterproportionale Entwicklung aus. Die Gesamtkosten steigen mit zunehmender produzierter Menge also immer langsamer. Für die Grenzkosten bedeutet das, dass diese mit steigender Produktionsmenge abnehmen. Ebenso verhält es sich mit den durchschnittlichen Kosten und den durchschnittlichen variablen Kosten.

Die angenommene Kostenfunktion K(x) = 3 +x ergibt folgende Graphenverläufe:

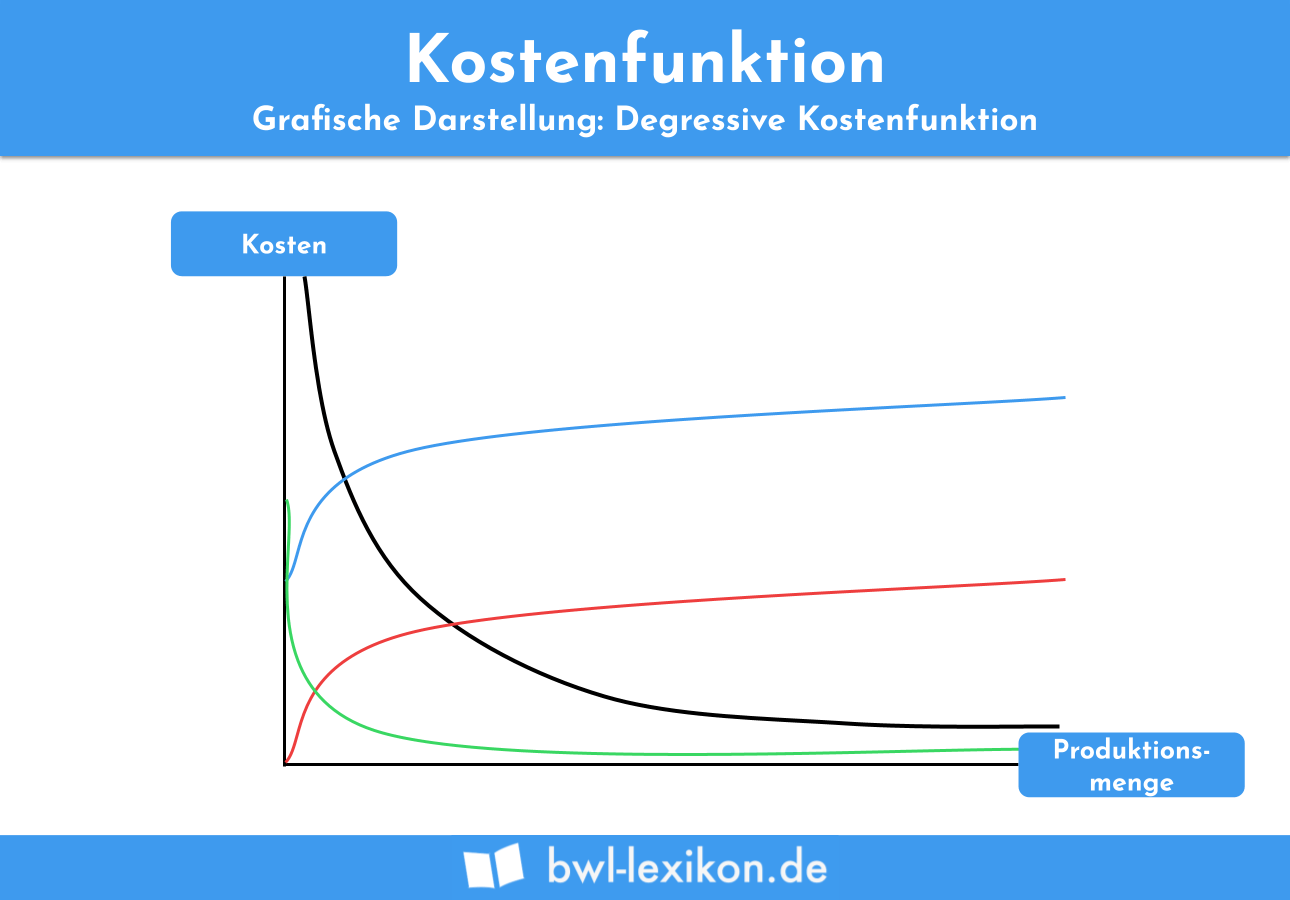
Kostenfunktion = Blau
variable Kosten = Rot
Grenzkosten / durchschnittliche variable Kosten = Grün
Durchschnittskosten = Schwarz

Degressive Kostenfunktionen kommen beispielsweise durch die Verhandlung von Mengenrabatten durch zunehmende Bestellmengen der Rohstoffe bei steigenden Produktionsmengen in der Realität vor.

Progressive Kostenfunktion

Liegt eine progressive vor, so steigen die variablen Kosten bei steigender Produktionsmenge überproportional an. Die Grenzkosten sind durch einen monoton steigenden Verlauf gekennzeichnet. Die Durchschnittskosten nehmen zunächst ab, steigen anschließend aber wieder an.

Nehmen wir die Kostenfunktion K(x) = 3 + x2 an, so ergeben sich folgende Verläufe im Graphen:

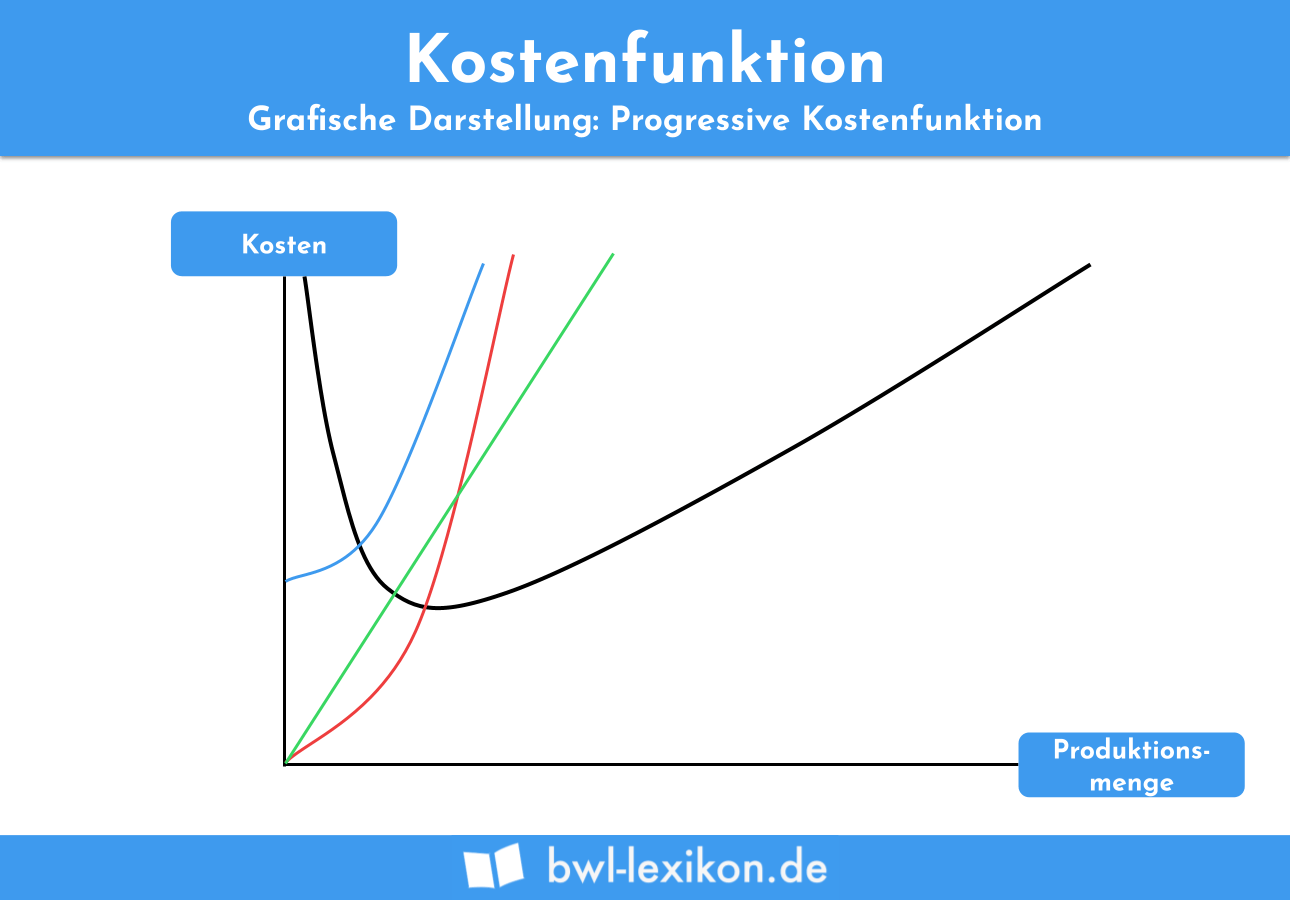
Kostenfunktion = Blau
variable Kosten = Rot
Grenzkosten / durchschnittliche variable Kosten = Grün
Durchschnittskosten = Schwarz

Progressive Kostenfunktionen kommen in der Realität zum Beispiel dann vor, wenn durch die Erhöhung der Produktionsmenge Zuschläge für Überstunden gezahlt werden müssen.

Regressive Kostenfunktion

Regressive Kostenfunktionen beschreiben eine Abnahme der Gesamtkosten bei zunehmender Produktionsmenge. Dadurch sinken auch die Grenzkosten und die Durchschnittskosten.

Die beispielhafte Kostenfunktion K(x) = 3 + 4x zeigt im Graphen folgende Verläufe:

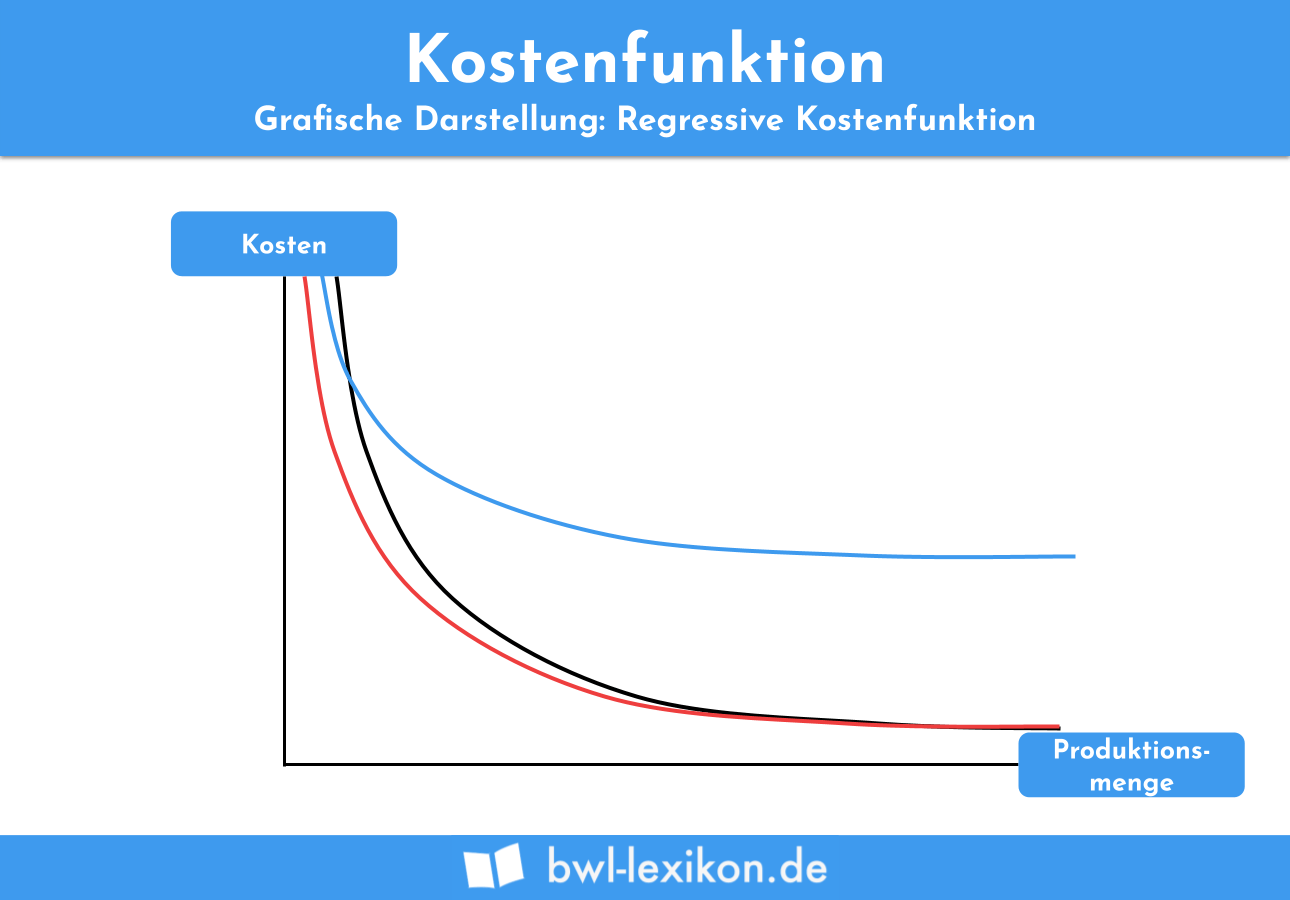
Kostenfunktion = Blau
Variable Kosten = Rot
Grenzkosten / durchschnittliche variable Kosten = Grün
Durchschnittskosten = Schwarz

Regressive Verläufe von Kostenfunktionen treten beispielsweise im Hinblick auf die Heizkosten in Unternehmen auf. Mit steigender Anzahl an Mitarbeitern können sich die Gesamtheizkosten reduzieren. In der Produktion trifft man aber äußerst selten auf regressive Kostenfunktionen.

Kostenfunktion

Welche Bedeutung hat die Kostenfunktion?