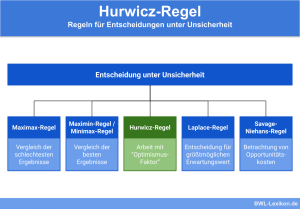
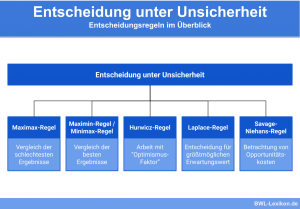
Die Laplace Regel beschreibt eine Entscheidungsregel für Entscheidungssituationen unter Unsicherheit. Da bei Entscheidungen unter Unsicherheit die Eintrittswahrscheinlichkeiten nicht bekannt sind, geht die Laplace Regel davon aus, dass alle möglichen Umweltzustände gleich wahrscheinlich sind. Die Handlungsalternative mit dem höchsten Erwartungswert ist in diesem Falle vorzuziehen.
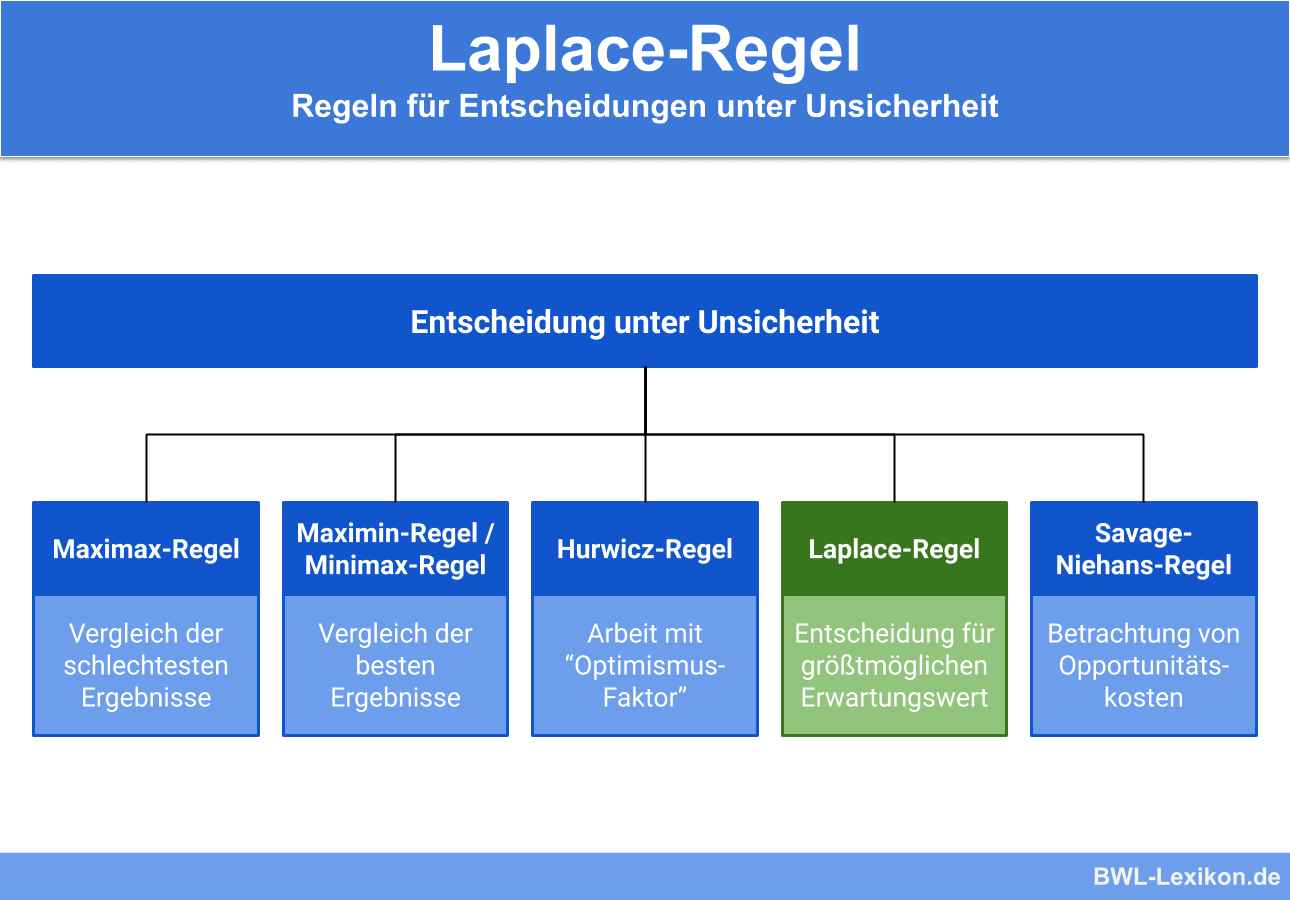
In diesem Kapitel lernst du, wann die Laplace Regel eine Rolle spielt und wie man sie anwendet. Außerdem stellen wir die Vor- und Nachteile dieser Entscheidungsregel gegenüber, sodass du nicht nur unsere Übungsaufgaben, sondern auch deine nächste Prüfung gut meistern kannst.
Warum ist die Laplace Regel wichtig?
Bei Entscheidungssituationen unter Unsicherheit liegen keine Informationen über die Wahrscheinlichkeit des Eintretens der einzelnen Umweltzustände vor. Daher gibt es nach dem Satz des unzureichenden Grundes auch keine Anhaltspunkte, um von unterschiedlichen Wahrscheinlichkeiten auszugehen.
Unter der Annahme gleicher Eintrittswahrscheinlichkeiten bietet die Laplace Regel eine einfache Methode zur Berechnung des Erwartungswertes einer jeden Handlungsalternative. Dementsprechend können auch Entscheidungen unter Unsicherheit mithilfe der Laplace Regel auf einer fundierten Grundlage getroffen werden.
Was ist die Laplace Regel?
Um fundierte Entscheidungen unter Unsicherheit treffen zu können, kann die Laplace Regel angewendet werden. In solchen Entscheidungssituationen sind zwar mögliche Handlungsalternativen, deren Ergebnisse sowie die möglichen Umweltzustände bekannt, allerdings fehlen Informationen über die Eintrittswahrscheinlichkeiten der jeweiligen Umweltzustände.
Da die Eintrittswahrscheinlichkeiten in einem solchen Szenario nicht bekannt sind, wendet man bei der Laplace Regel den Satz des unzureichenden Grundes an. Das bedeutet, dass es keinen Grund gibt davon auszugehen, dass das Eintreten von einem der Umweltzustände wahrscheinlicher ist als das Eintreten eines der anderen.
Den möglichen Umweltzuständen werden also die gleichen Eintrittswahrscheinlichkeiten zugewiesen. Die eigentliche Entscheidung wird dann anhand der Erwartungswert-Regel getroffen. Dabei ist diejenige Handlungsalternative als optimal anzusehen, welche den höchsten Erwartungswert aufweist. Der Erwartungswert ergibt sich aus der Summe der Produkte von zu erwartendem Ergebnis und Entrittswahrscheinlichkeit.
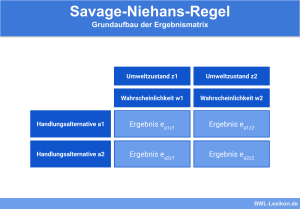
Zur Anwendung der Laplace Regel erstellt man zuerst eine Ergebnis- bzw. Nutzenmatrix:
| Umweltzustand z1 mit Eintrittswahrscheinlichkeit w1 | Umweltzustand z2 mit Eintrittswahrscheinlichkeit w2 | |
| Handlungsalternative a1 |  |  |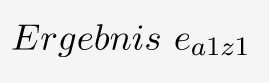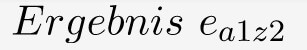
| Handlungsalternative a2 |  |  |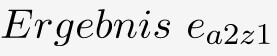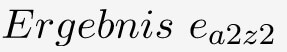
Den jeweiligen Umweltzuständen werden die gleichen Wahrscheinlichkeiten zugewiesen, in diesem Fall also jeweils 50 %.
Zur Berechnung des Erwartungswert ergibt sich folgende Formel:
![\[ Erwartungswert~von~a1 = (e_{a1z1} * w1) + (e_{a1z2} * w2) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-c2a5582dbcf6225b3bd6610318bd6833_l3.png "Rendered by QuickLaTeX.com")
![\[ Erwartungswert~von~a2 = (e_{a2z1} * w1) + (e_{a2z2} * w2) \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-6ea69c37f2b06cf74e6570e6647c5f56_l3.png "Rendered by QuickLaTeX.com")
Diejenige Handlungsalternative, welche den höchsten Erwartungswert ergibt, ist zu präferieren.
Aus der Entwicklungsabteilung bekommt sie folgende Vorschläge:
- Die Einführung eines neuen Schokoriegels (Handlungsalternative 1)
- Die Einführung eines Bio-Frucht-Müsli-Riegels (Handlungsalternative 2)
Da die “Naschdichsatt AG” über keine gut aufgestellte Marktforschungsabteilung verfügt, ist dem Unternehmen nicht genau klar, ob sich der Trend hin zu gesunder Ernährung und gesundem Naschen in den nächsten Jahren fortsetzen wird (Umweltzustand 1) oder nicht (Umweltzustand 2).
Lediglich die zu erzielenden Umsätze der einzelnen Produkte können von der Vertriebsabteilung vorausgesagt werden:
- Umsatz des Schokoriegels bei anhaltendem Trend: 50.000 €
- Umsatz des Schokoriegels bei zurückgehendem Trend: 150.000 €
- Umsatz des Bio-Frucht-Müsli-Riegels bei anhaltendem Trend: 160.000 €
- Umsatz des Bio-Frucht-Müsli-Riegels bei zurückgehendem Trend: 30.000 €
Die bekannten Parameter werden in eine Entscheidungsmatrix eingetragen:
| anhaltender Trend | zurückgehender Trend | |
| Schokoriegel | 50.000 € | 150.000 € |
| Bio-Frucht-Müsli-Riegels | 160.000 € | 30.000 € |
Nach der Laplace Regel ist es genauso wahrscheinlich, dass der Trend zu gesunder Ernährung anhält wie die Tatsache, dass dieser zurückgeht. Die Eintrittswahrscheinlichkeit für beide möglichen Umweltzustände beträgt also 50 %.
Die jeweiligen Erwartungswerte lassen sich also folgendermaßen berechnen:
![\[ Erwartungswert~a1: (50.000~Euro * 0,5) + (150.000~Euro * 0,5) = 100.000 € \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-83db674684babf8ff9ff3e0bbfeddfac_l3.png "Rendered by QuickLaTeX.com")
![\[ Erwartungswert~a2: (160.000~Euro * 0,5) + (30.000~Euro * 0,5) = 95.000 € \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-50b717d3caac916cea6704519a6bfa98_l3.png "Rendered by QuickLaTeX.com")
Die Geschäftsführung der “Naschdichsatt AG” entscheidet sich in diesem Fall also für die Einführung des neuen Schokoriegels, da dieser den höheren Erwartungswert verspricht.
Vorteile und Nachteile der Laplace Regel
- Die Laplace Regel bietet eine einfach zu berechnende Entscheidungsgrundlage für Entscheidungssituationen unter Unsicherheit.
- Die Entscheidungsfindung wird vereinfacht und somit das Risiko einer Fehlentscheidung vermindert.
- Die Laplace Regel geht von einer gleichen Verteilung der Eintrittswahrscheinlichkeiten der Umweltzustände aus. In der Realität ist das selten der Fall. Das Unternehmen sollte eher Anstrengungen unternehmen, um, falls möglich, mehr Informationen über die Wahrscheinlichkeiten des Eintretens der Umweltzustände zu beschaffen.
Übungsaufgaben
#1. Was ist die Laplace Regel?
#2. Was ist einer der Nachteile der Laplace Regel?
#3. “Die Laplace Regel kann in Entscheidungssituationen unter Sicherheit angewendet werden.”- Diese Aussage ist:
#4. “Der Erwartungswert ergibt sich aus der Summe der Produkte von Ergebnis und Eintrittswahrscheinlichkeit.” – Diese Aussage ist:
#5. “Bei der Laplace Regel muss der Entscheider die einzelnen Eintrittswahrscheinlichkeiten der Umweltzustände selbst festlegen” – diese Aussage ist:
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
