Branch and Bound

Enthält: Beispiele · Definition · Grafiken · Übungsfragen

Branch and Bound nennt sich ein mathematisches Verfahren zur Lösung von ganzzahligen Optimierungsproblemen im Bereich des Operations Research. Durch das Aufspalten (Branch) der zulässigen Lösungsmenge in Teilmengen und das frühzeitige Aufstellen geeigneter Schranken (Bound) soll der mögliche Lösungsraum möglichst klein gehalten werden, um unnötig lange Rechenzeiten zu vermeiden.

In diesem Kapitel erläutern wir dir das Branch and Bound Verfahren und zeigen anhand eines Beispiels, wie dieses angewendet wird. Mit Hilfe der anschließenden Übungsaufgaben kannst du herausfinden, wie gut dein Wissen in diesem Bereich aufgestellt ist.

Synonym: Branch-and-Bound-Algorithmus

Warum ist das Branch and Bound Verfahren wichtig?

Das Branch and Bound Verfahren kann dann genutzt werden, wenn für Probleme die optimale Lösung gefunden werden soll. Im Gegensatz zu anderen Optimierungsverfahren im Operations Research kann es nur genutzt werden, wenn es sich um ein ganzzahliges Problem handelt.

In der betrieblichen Realität gibt es dafür zahlreiche Anwendungsbeispiele. So können beispielsweise in der Produktion immer nur ganze Produkte hergestellt werden. Die Produktion von 10,5 Laptops beispielsweise ist genauso wenig möglich, wie der Einsatz von 3,4 Arbeitern.

Daher bietet sich für das Branch and Bound Verfahren eine ganze Reihe möglicher Einsatzfelder, beispielsweise:

Durch das immer weitere Beschränken der möglichen Lösungsmenge wird im Branch and Bound Verfahren unnötiger Rechenaufwand vermieden.

Was versteht man unter Branch and Bound?

Beim Branch and Bound wird die Suche nach der optimalen Lösung eines ganzzahligen Problems in zwei Schritten durchgeführt:

  1. Branch (Aufteilung)
  2. Bound (Schranke)

Der Verzweigungsschritt (Branch)

Durch den Verzweigungsschritt (Branch) wird das zu lösende Problem in kleinere Teilprobleme aufgeteilt, um es zu vereinfachen. Dadurch entsteht die Aufstellung eines Entscheidungsbaums.

Um den nächsten zu untersuchenden Baumknoten zu ermitteln, können folgende Verfahren angewendet werden:

  • Die Tiefensuche:
    Es wird dasjenige Teilproblem betrachtet, welches als letztes im Baum hinzugekommen ist. So kann der Baum schnell in die Tiefe bearbeitet werden und man erhält schnell eine zulässige Lösung. Allerdings muss diese nicht unbedingt die beste sein.
  • Die Breitensuche:
    Bei dieser Methode werden zuerst alle Knoten einer Ebene des Baumes betrachtet, bevor die tiefer liegenden Ebenen in Betracht gezogen wird. Zwar ist der Zeitaufwand hierbei wesentlich größer als bei der Tiefensuche, die Qualität der gefundenen Lösung dafür umso besser.
  • Die Bestensuche:
    Im Zuge der Bestensuche wird dasjenige Teilproblem mit der besten unteren Schranke betrachtet. Das Ziel dabei ist es, möglichst schnell die beste Lösung zu erhalten.

Der Abgrenzungsschritt (Bound)

Mit dem Schritt der Abgrenzung werden bestimmte Äste des aufgestellten Baumes “abgeschnitten”. Somit werden sie in der weiteren Suche nach der optimalen Lösung nicht weiter betrachtet. Mit diesem Schritt wird die zulässige Lösungsmenge verkleinert, um den Rechenaufwand zu minimieren.

Um dies zu erreichen, werden zwei Schranken miteinander verglichen. Die untere Schranke ist dabei durch den Weg von der Baumwurzel hin zu einem der Teilprobleme gekennzeichnet. Die obere Schranke ist die vorerst bestmögliche Lösung. Liegt die untere Schranke über der bisher besten Lösung, so kann der gesamte Zweig der oberen Schranke “abgeschnitten” werden, da sicher ist, dass es mindestens eine bessere Lösung gibt.

Anwendung des Branch and Bound Verfahrens bei kombinatorisch ganzzahligen Problemen

Anhand des folgenden Beispiels wollen wir dir die Anwendung des Branch and Bound Verfahrens erläutern:

Beispiel
Gegeben ist folgendes Optimierungsproblem:

    \[ max~f(x) = 3x_1+x_2 \]

Nebenbedingungen:

    \[ 4x_1+3x_2 \leq 12 \]

    \[ 2x_1 + 5x_2 \leq 10 \]

Es gilt ebenfalls die Nichtnegativitätsbedingung für x1 und x2:

    \[ x_1,x_2 \geq 0 \]

Anhand des Koordinatensystems können wir den möglichen Lösungsraum erkennen:

Die Branch and Bound Methode dient nun dazu, den möglichen Lösungsraum soweit einzuschränken, bis die bestmögliche Lösung gefunden ist. Zunächst wird dazu die optimale Lösung des Problems ermittelt.

Durch Einsetzen und Auflösen der Gleichungen können die Variablen berechnet werden:

    \[ x_1 = 2,14 \]

    \[ x_2 = 1,143 \]

Anschließend werden diese in die Zielfunktion eingesetzt werden. So erhalten wir:

    \[ f(x) = 7,57 \]

Dies ist allerdings nur das vorerst optimale Ergebnis, da es sich hierbei nicht um eine ganzzahlige Zahl handelt. Somit bildet es die obere Schranke für die Anwendung des Branch and Bound Verfahrens.

Als nächstes wird die untere Schranke gesucht. Aufgrund der Nichtnegativitätsbedingung unseres Optimierungsproblems. Durch das Branching wird das Ursprungsproblem (P0) nun in zwei Teilprobleme verzweigt.

Dazu wird die optimale Lösung von der nächstgrößeren ganzen Zahl subtrahiert:

    \[ 3 - 2,14 = 0,86 \]

    \[ 2 - 1,143 = 0,857 \]

Anschließend entsteht eine erste Verzweigung (Bounding) in unserem Entscheidungsbaum anhand der Zahl mit der größten Differenz. Es besteht nun die Möglichkeit, dass x1 entweder größer gleich 3 oder kleiner gleich 2 ist.

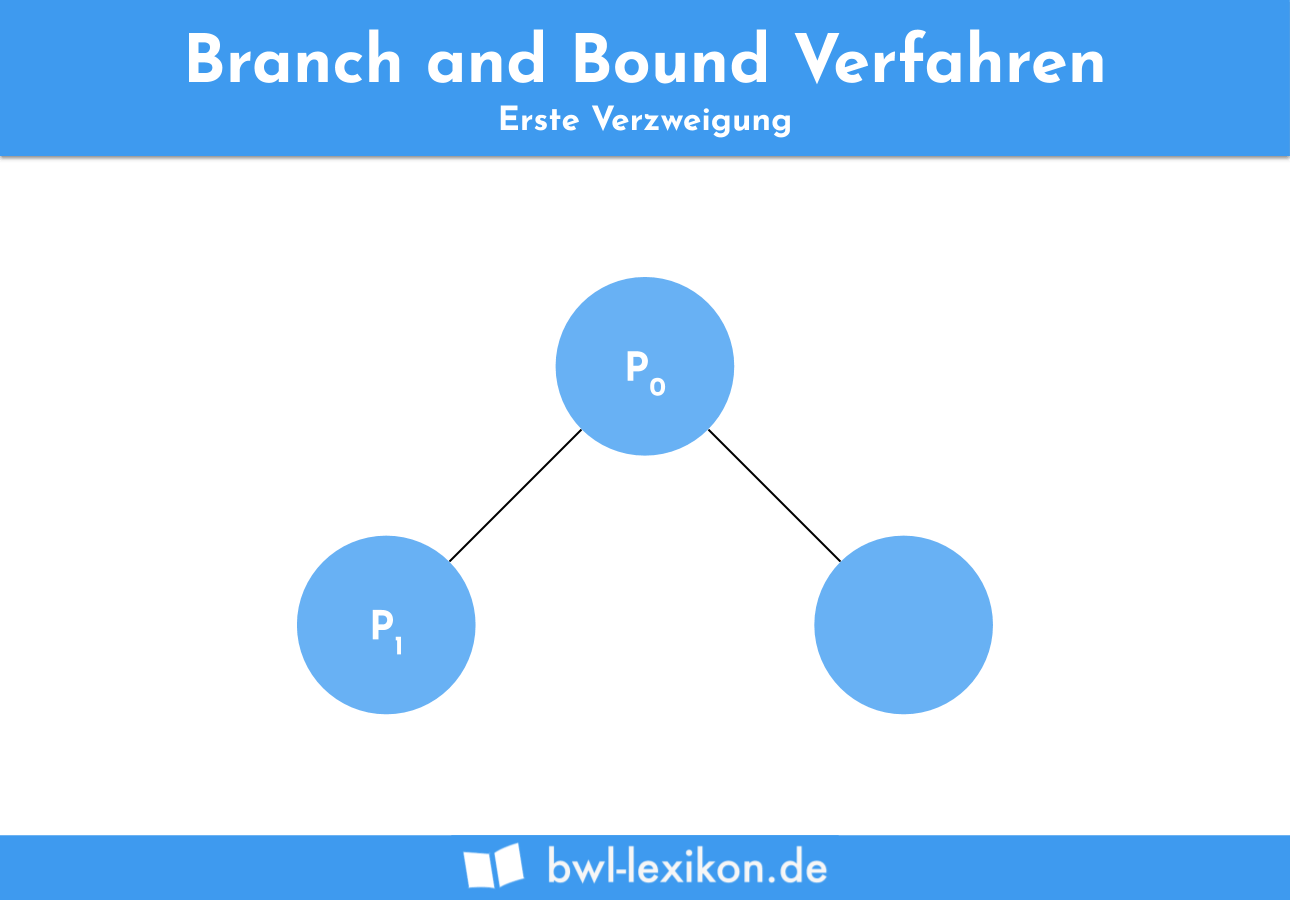
Branch and Bound Verfahren: Erste Verzweigung
Branch and Bound Verfahren: Erste Verzweigung

Nach dem Prinzip der Tiefensuche betrachten wir als erstes das Problem, welches zuletzt in den Entscheidungsbaum eingezeichnet wurde (P1).

Mit dem neuen Wert x1 = 2 berechnen wir nun erneut den Wert der Zielfunktion. F(x) beträgt nun 7,143. Wir nähern uns also einer ganzzahligen Zahl an. Auch x2 muss nun noch an die neuen Einschränkungen angepasst werden.

Durch Gleichsetzen und auflösen erhalten wir nun:

    \[ x_2 = 1,2 \]

Beide Werte erneut in die Zielfunktion eingesetzt ergibt:

    \[ f(x) = 7,2 \]

x2 ist aber immer noch nicht ganzzahlig, weshalb ein weiterer Verzweigungsschritt vorgenommen werden muss. Unser P1 muss also in zwei weitere Teilprobleme aufgeteilt werden.

Es besteht sowohl die Möglichkeit, dass x2 größer gleich 2 oder aber kleiner gleich 1 ist:

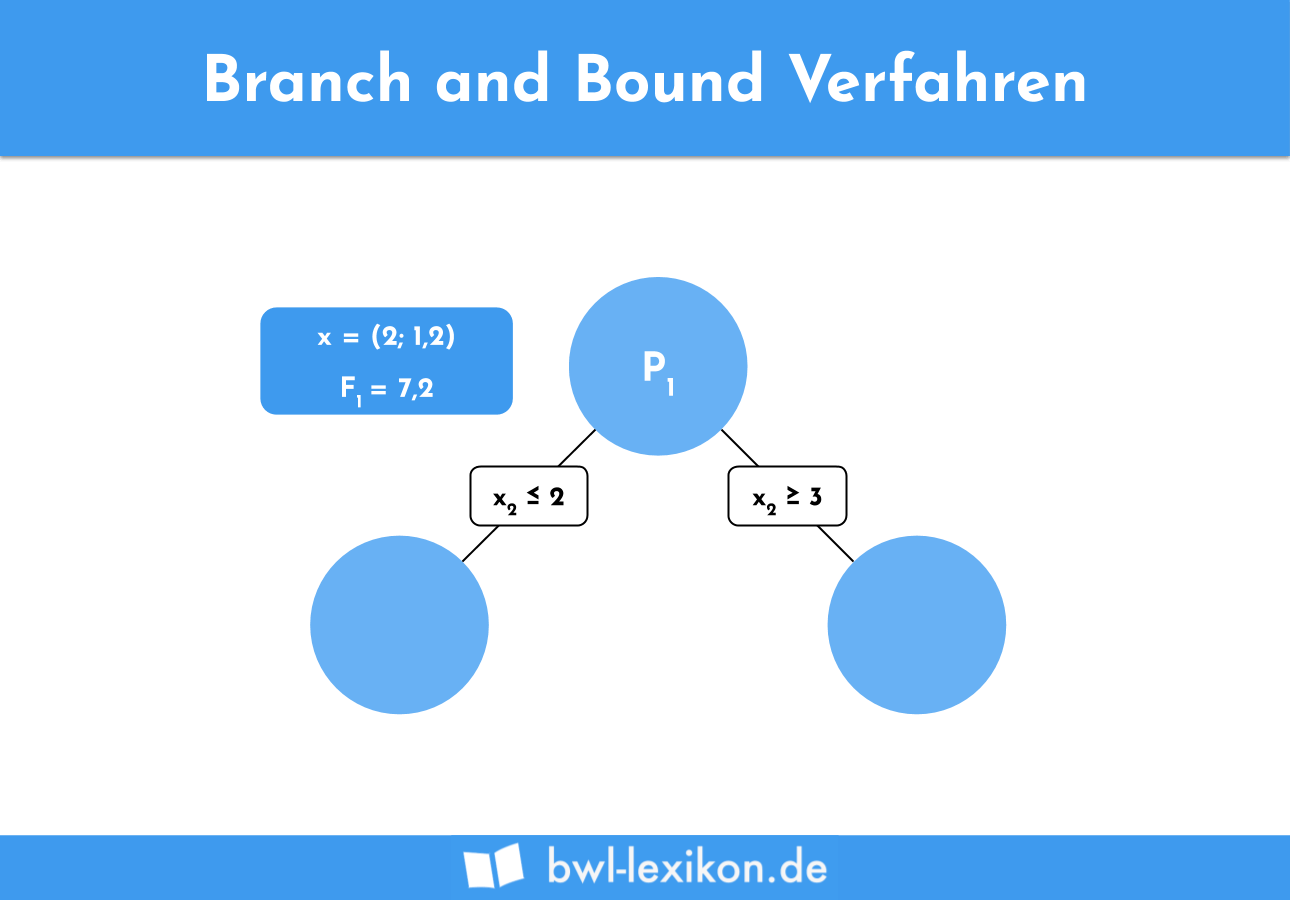
Branch and Bound Verfahren - Schritt 2
Branch and Bound Verfahren – Schritt 2

Nach der Last-In-First-Out-Regel der Tiefensuche ist x nun (2;1). Eingesetzt in die Zielfunktion ergibt dies für P2 den Wert 7. Dies stellt die neue untere Schranke dar, da es sich um eine zulässige Lösung mit ganzzahligen Variablen handelt. Wir wissen also, dass der Zielfunktionswert in den anderen Teilproblemen nicht schlechter als 7 sein darf.

Nehmen wir nun die rechte Seite unserer Verzweigung als P3 an, in dem x2 größer gleich 2 sein soll. Eingesetzt in die Zielfunktion ergibt sich der Wert 8, welcher nicht im Bereich der zulässigen Lösungen liegt. Wir können diesen Zweig also ausschließen.

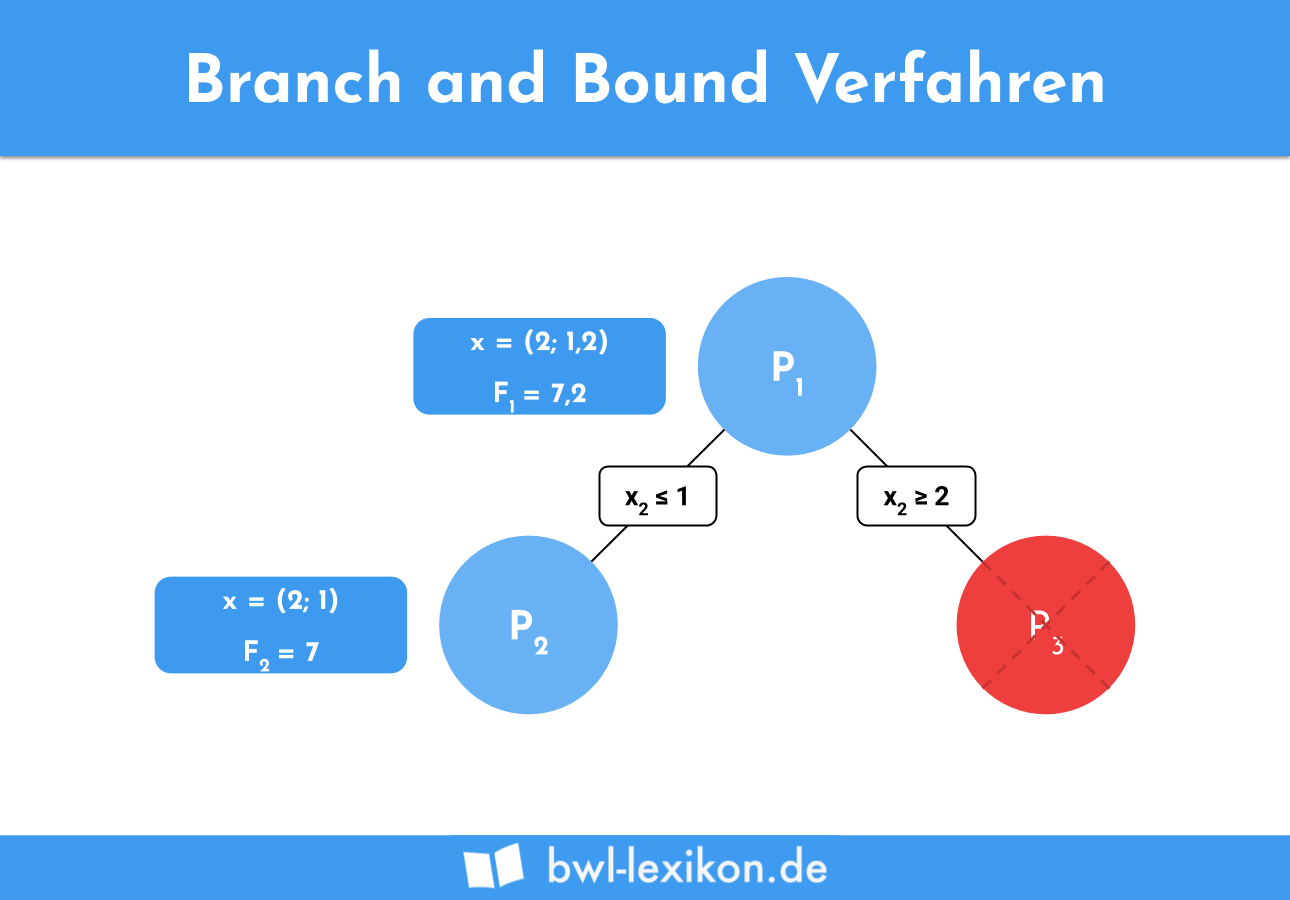
Branch and Bound Verfahren - Schritt 3
Branch and Bound Verfahren – Schritt 3

Um die bestmögliche Lösung zu finden, kehren wir in die obere Ebene des Baumes zurück. Die hier noch offene Verzweigung ist unser P4

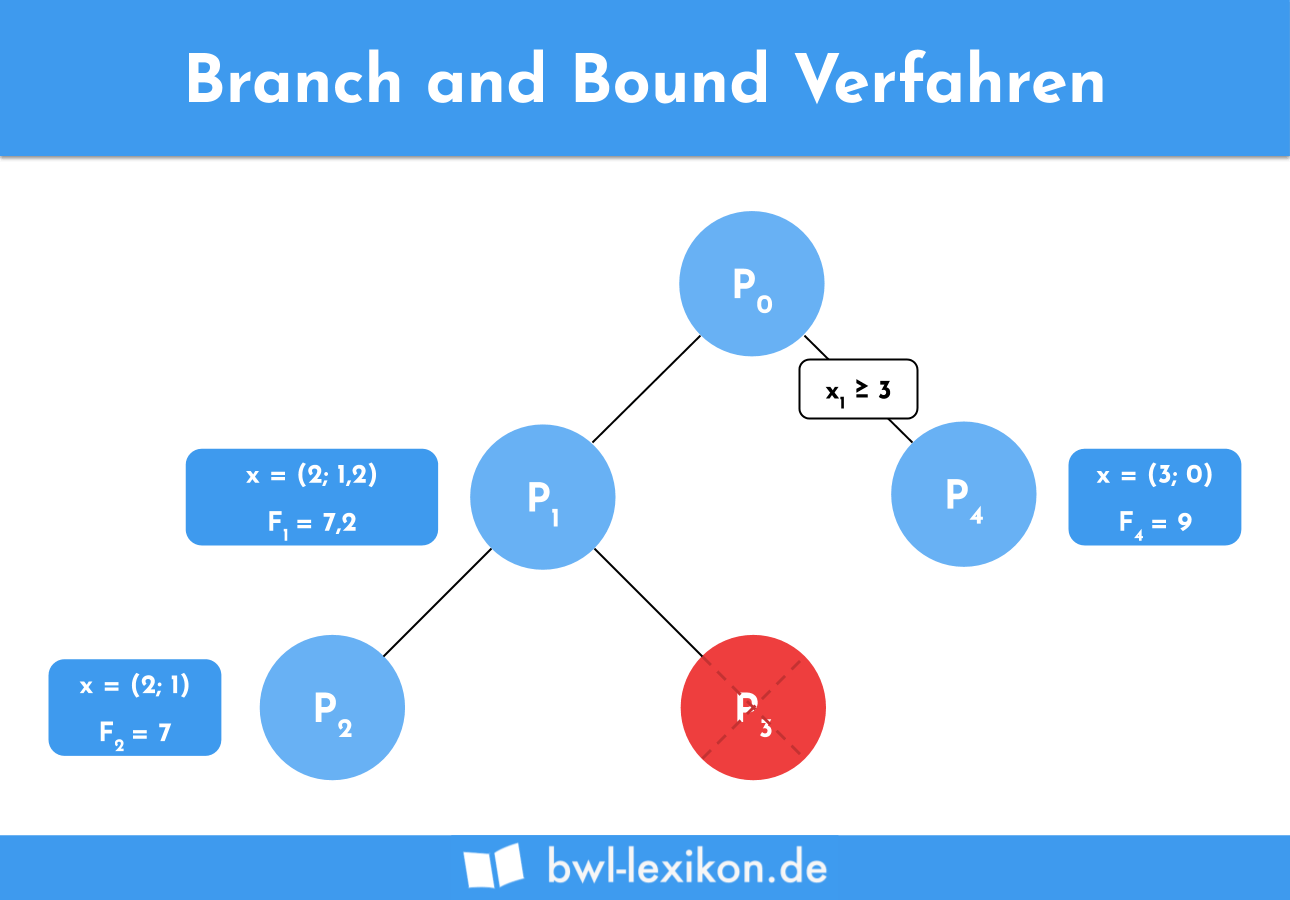
Branch and Bound Verfahren - Schritt 4
Branch and Bound Verfahren – Schritt 4

Die hier noch offene Möglichkeit ist x1 größer gleich 3. Gleichgesetzt und aufgelöst ergibt dies für x2 den Wert 0. Der Zielfunktionswert beträgt damit 9 und liegt auch außerhalb unserer zulässigen Lösungsmenge.

Die bestmögliche Lösung ist also bereits gefunden und heißt:

    \[ x = (2;1) \]

Anwendung des Branch and Bound Verfahrens bei binären kombinatorisch ganzzahligen Problemen

Auch ein binäres kombinatorisches ganzzahliges Problem lässt sich mit dem Branch and Bound Verfahren lösen. Auch das zeigen wir dir an einem Beispiel:

Beispiel
Die “Schmuckmanufaktur Edelgold” möchte entscheiden, welche Produkte in dieser Woche hergestellt werden sollen. Zur Auswahl stehen: Ohrringe, Armband und eine Kette.

Jedes Produkt verspricht einen anderen Deckungsbeitrag (Nutzen):

  • Ohrringe: 16 €
  • Armband: 12 €
  • Kette: 20 €

Allerdings stehen für die Produktion nur 30 Arbeitsstunden zur Verfügung, da die restliche Zeit die Werkstatt aufgeräumt werden muss.

Für die Produkte werden unterschiedliche Zeiten benötigt:

  • Ohrringe: 8 Stunden
  • Armband: 10 Stunden
  • Kette: 20 Stunden

Die Zielfunktion lautet demnach:

    \[ f(x) = 16x_1 + 12x_2 +20x_3 \]

Außerdem unterliegt die Schmuckmanufaktur Edelgold der Restriktion, dass die Rohstoffe in dieser Woche nur jeweils für ein Stück der jeweiligen Produkte ausreichen. Die Anzahl der Produkte xi muss also eine binäre Variable 0 oder 1 sein, also entweder wird produziert oder es wird nicht produziert.

Um das Branch and Bound Verfahren anwenden zu können, muss den Produkten eine Priorität zugewiesen werden, damit entschieden werden kann, nach welcher Variable verzweigt werden soll. Dazu wird der relative Nutzen bestimmt.

Dieser ergibt sich aus dem Nutzen geteilt durch den Aufwand:

  • Ohrringe: 16 / 8 = 2 → Prio 1
  • Armband: 12 / 10 = 1,2 → Prio 2
  • Kette: 20 / 20 = 1 → Prio 3

Sind die Prioritäten festgelegt, kann das Branch and Bound Verfahren gestartet werden.
Die untere Schranke beträgt 0 Stunden. Die obere Schranke wird anhand der ermittelten Priorität festgelegt.

  • x1 (Ohrringe) hat die Prio 1 und lasten die Manufaktur mit 8 Stunden aus.
  • x2 (Armband) mit Prio 2 bringt zusätzliche 10 Stunden Auslastung, womit nur noch 12 Stunden zur Verfügung stehen.
  • Eine vollständige Herstellung von x3 mit 20 Stunden kann also nicht mehr durchgeführt werden. Demnach kann x3 nur noch zu 6/10 hergestellt werden.

Eingesetzt in die Zielfunktion ergibt das:

    \[ f(x) = 16+12+(\frac{6}{10}*20)=40 \]

40 Stellt also die obere Schranke dar.

Vom Ursprungsproblem P0 ausgehend wird nun nach der “Maximum-Upper-Bound-Regel” verzweigt. So werden direkt die Schranken aller Teilprobelme ermittelt. Entsprechend der festgelegten Prioritäten wird nun verzweigt, beginnend also mit x1. In P1 (x1=1) ändert sich der Zielfunktionswert nicht, da bereits in P0 x1 = 1 ist.

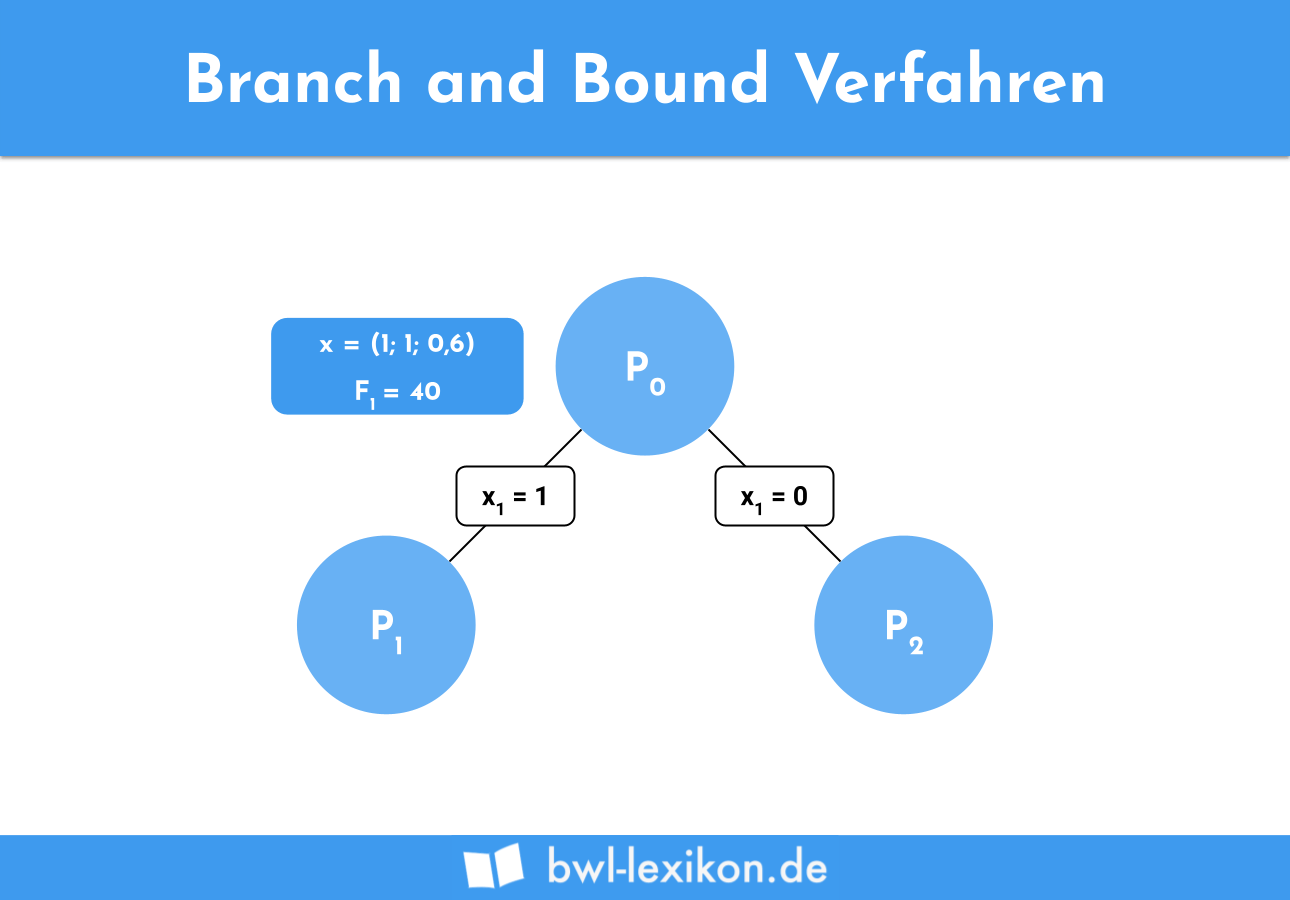
Branch and Bound Verfahren - Schritt 5
Branch and Bound Verfahren – Schritt 5

Anschließend wird P2 berechnet. Da x1 hier gleich 0 ist, also nicht produziert wird, nehmen wir vollständig x2 und x3 auf. Dies ergibt einen Wert von 30 Stunden, welcher noch in unserem zulässigen Lösungsraum liegt.

In die Zielfunktion eingesetzt, erhalten wir einen Zielfunktionswert von 32. Dieser Wert bildet die untere Schranke, d.h. der Zielfunktionswert der anderen Teilprobleme darf nicht geringer sein.

Anschließend wird P1 weiter nach der nächsten Priorität verzweigt. In P3 ändert sich also nichts im Vergleich zu P1.

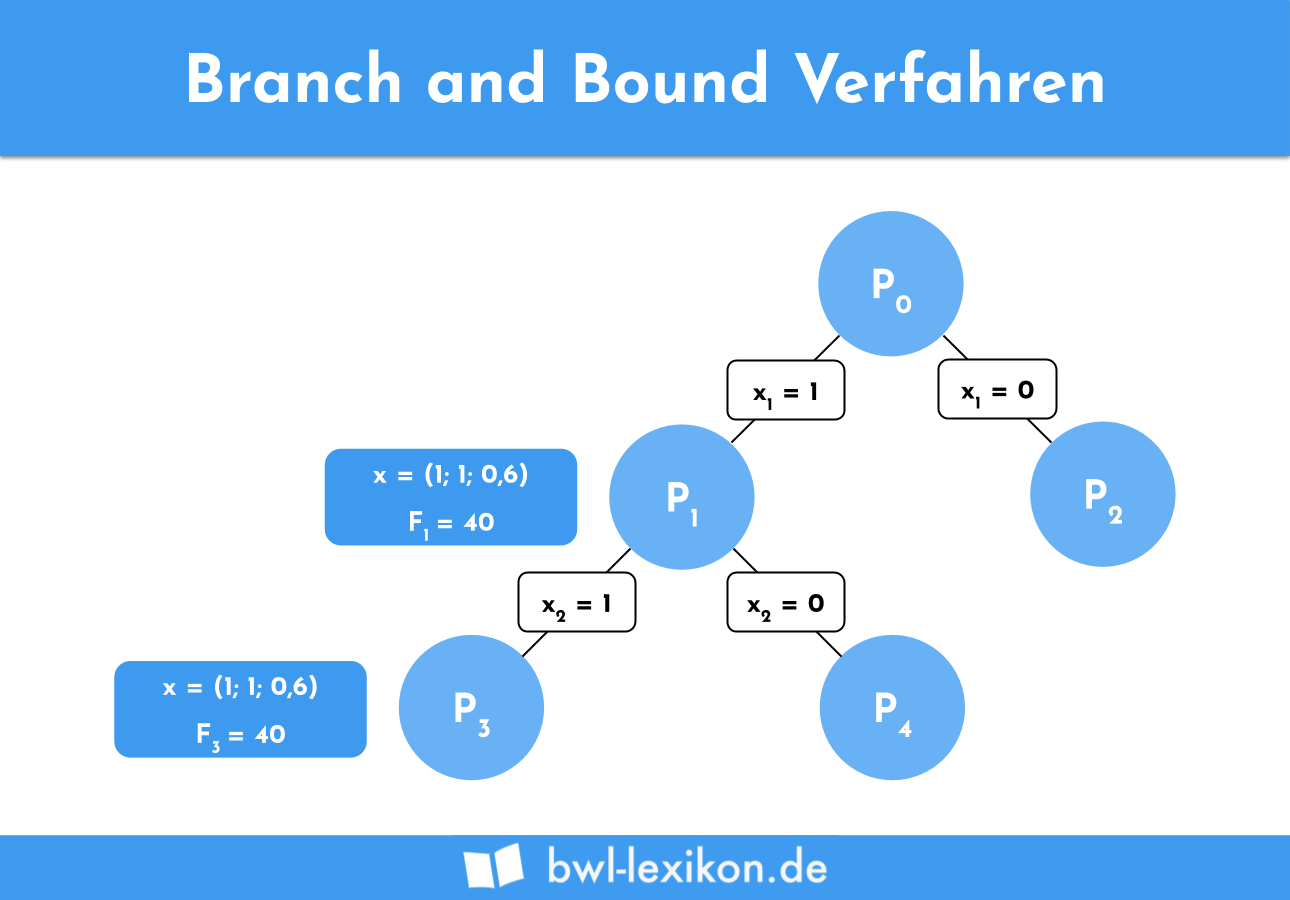
Branch and Bound Verfahren - Schritt 6
Branch and Bound Verfahren – Schritt 6

In P4 wird x2 allerdings nicht produziert, ist also null.

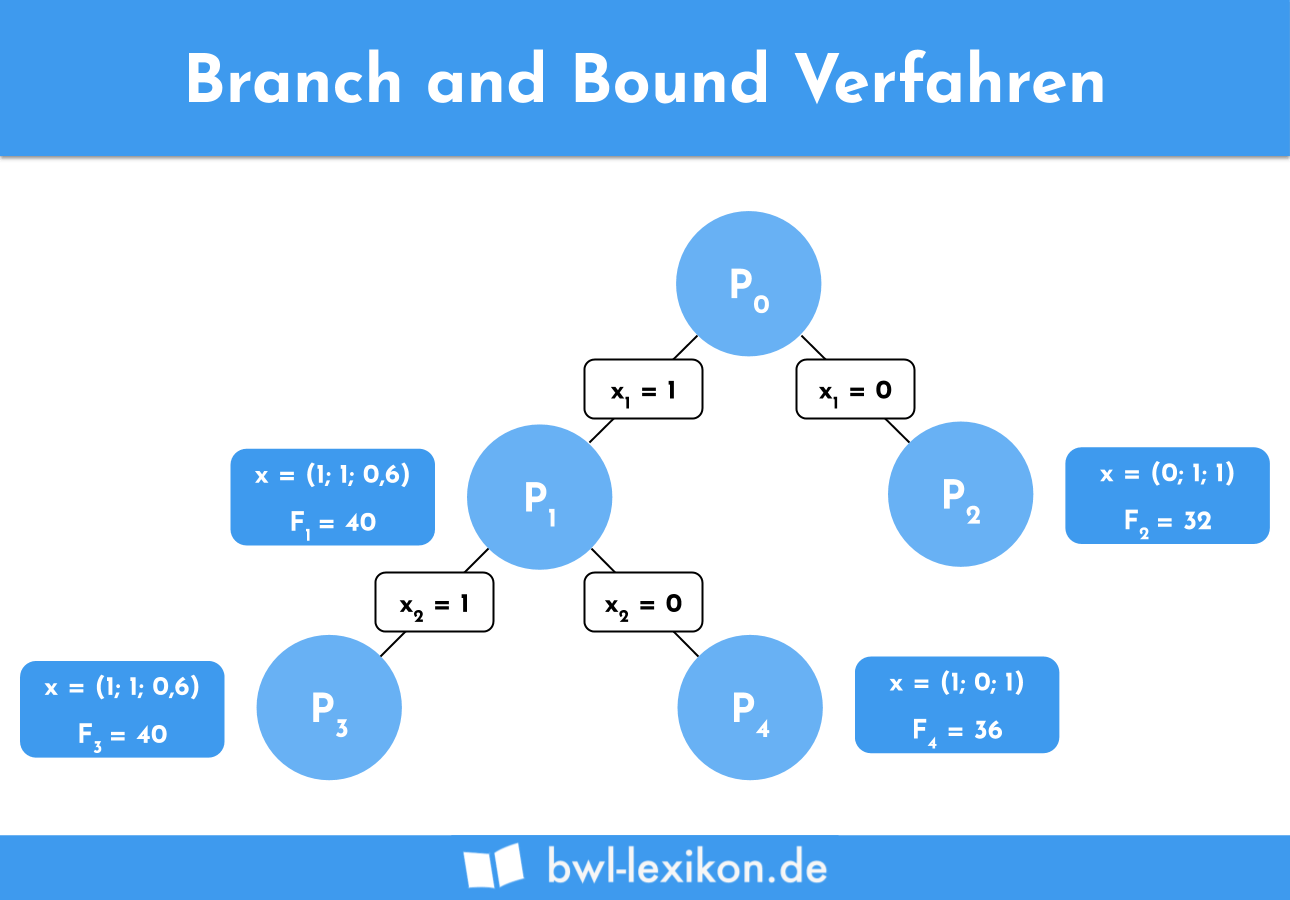
Branch and Bound Verfahren - Schritt 7
Branch and Bound Verfahren – Schritt 7

Eingesetzt in die Zielfunktion ergibt sich der Zielfunktionswert 36. Entsprechend der Maximum-Upper-Bound-Regel wird das Problem mit der höheren oberen Schranke als nächstes betrachtet. P5 mit x3 gleich 1 ist allerdings unzulässig, da die maximale Kapazität damit überschritten wird. In P6 ist x3 gleich 0, was einen Zielfunktionswert von 28 ergibt.

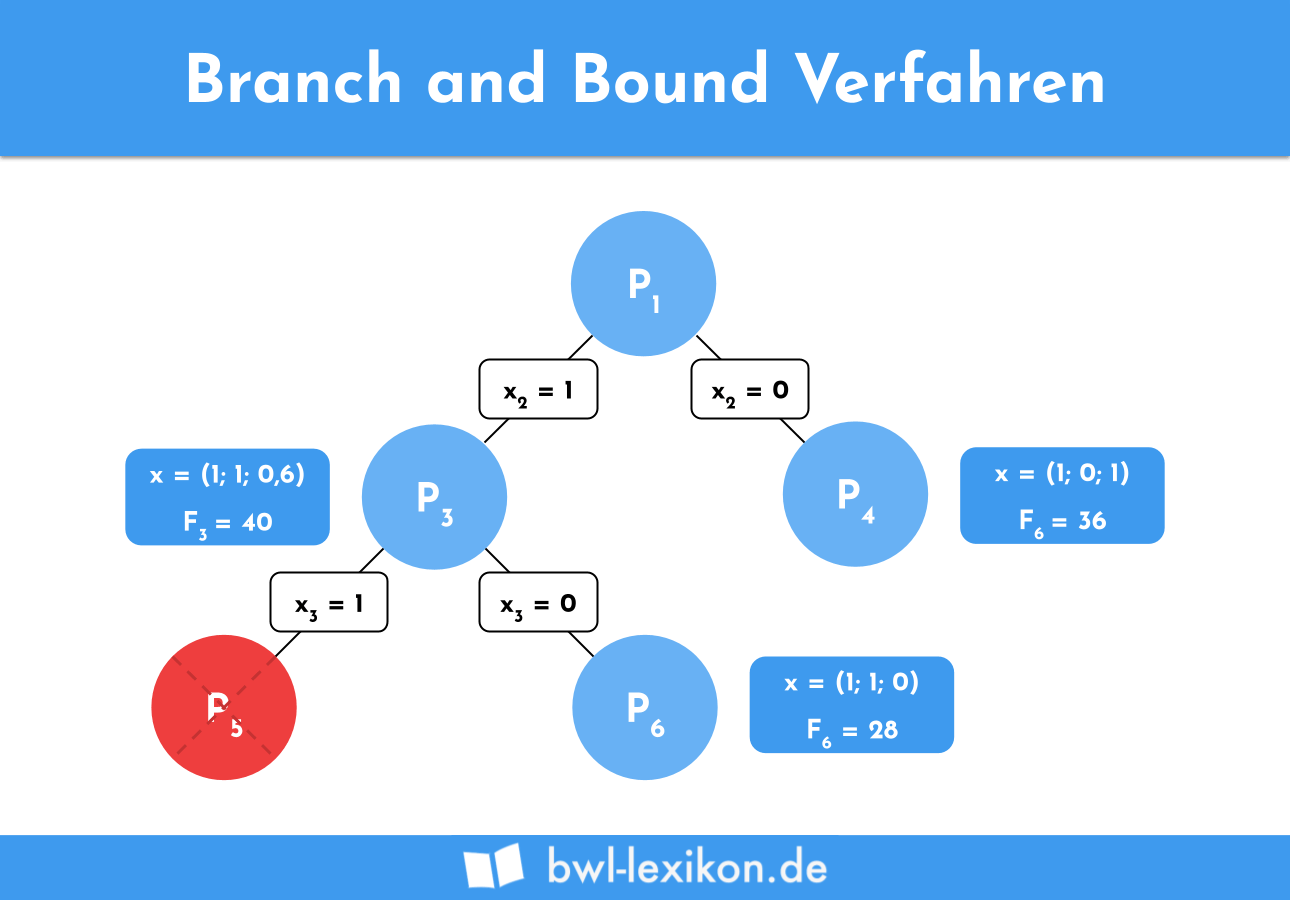
Branch and Bound Verfahren
Branch and Bound Verfahren

An dieser Stelle erkennt man, dass der Zielfunktionswert bereits unter der höchsten Schranke liegt. Der maximal zu erreichende Nutzen liegt also bei 36 in P4. Demnach sollten die Ohrringe und das Armband angefertigt werden.

Vor- und Nachteile des Branch and Bound Verfahrens

Vorteile:

  • unterschiedlichste Optimierungsprobleme sind lösbar
  • Prioritäten können selbst festgelegt werden
Nachteile:

  • hoher Rechenaufwand trotz dem Ausschluss ungünstiger Verzweigungen

Übungsfragen

#1. Was versteht man unter Branch and Bound?

#2. Welches Ziel verfolgt das Branch and Bound Verfahren?

#3. “Das Branch and Bound Verfahren gehört zu den Optimierungsverfahren im Operations Research” - Diese Aussage ist:

#4. “Beim Branch and Bound Verfahren werden ungünstige Lösungen nicht weiter in die restliche Betrachtung mit einbezogen.” - Diese Aussage ist:

#5. “Das Branch and Bound Verfahren eignet sich besonders gut für nicht ganzzahlige Probleme.” - diese Aussage ist:

Fertig

Ergebnisse

Könnte dich auch interessieren:

Operations Research: Beispiel

Operations Research

Das Operations Research dient der Unterstützung von Entscheidungsprozessen mit Hilfe mathematischer Methoden. Es beschreibt die stetige Untersuchung der Handlungen im … weiterlesen >>

Varianten des Simplex-Verfahrens

Simplex-Verfahren

Das Simplex Verfahren gehört zu den Optimierungsmethoden im Operations Research zur Findung einer optimalen Lösung von linearen Optimierungsproblemen. Dieses Kapitel … weiterlesen >>

Delphi Methode: Einsatzbereiche

Delphi Methode

Als Delphi-Methode wird ein Verfahren zur Abschätzung zukünftiger Entwicklungen bezeichnet, bei dem in einem mehrstufigen Verfahren Experten auf dem jeweiligen … weiterlesen >>

Nichts passendes dabei?

Erkunde andere Fachbereiche oder benutze die Suchfunktion. Falls Du keine Antwort auf Deine Frage findest, schick uns gerne eine Nachricht, wir versuchen dann passenden Content für Dich zu schaffen.

Zur Übersicht
Oder lieber die Suche benutzen?