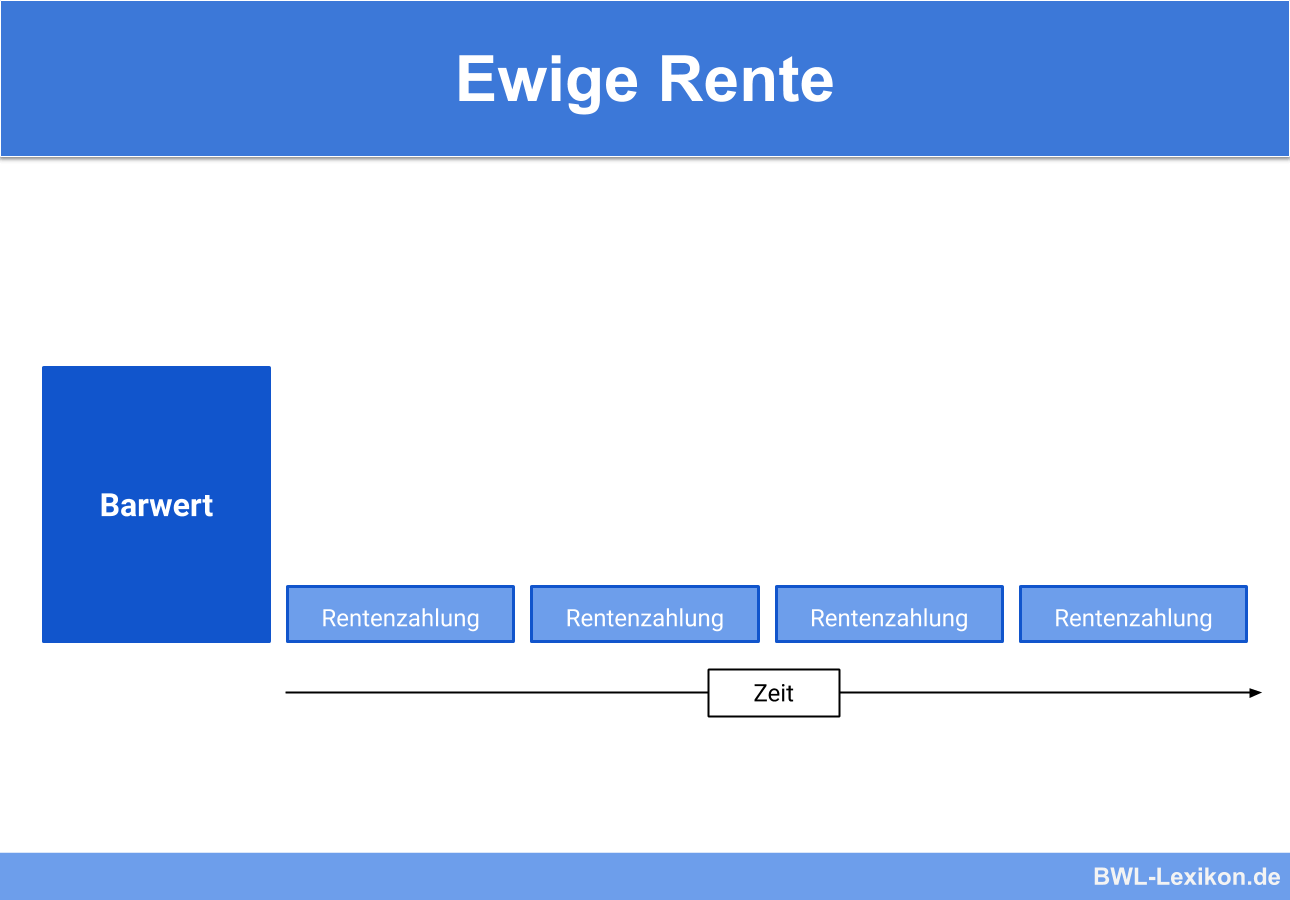
Die ewige Rente ist eine fortlaufend, periodisch ausgezahlte Rente, die den Wert der Kapitaleinlage nicht verändert. Sie wird unbegrenzt lange ausbezahlt und unterliegt somit keiner zeitlichen Begrenzung. Vor allem in der Unternehmens- und Immobilienbewertung ist die finanzmathematische Berechnung der ewigen Rente von großer Bedeutung. Denn auch hier gilt die Annahme, dass das Unternehmen und die Immobilie unendlich lange bestehen bleibt. Die Errechnung des Rentenbarwerts führt in weiterer Folge zur genauen Bewertung des Betriebes.
In der folgenden Lektion erfährst du, welche finanzmathematische Größe sich hinter dem Begriff der „ewigen Rente“ verbirgt und in welchen Bereichen er Anwendung findet. Am Ende der Lektion findest du außerdem hilfreiche Übungsaufgaben zum soeben Erlernten.
- Synonyme: Perpetuität
- Englisch: perpetual annuity
Inhalt dieser Lektion
Warum ist die ewige Rente wichtig?
Die Berechnung der ewigen Rente und des daraus resultierenden Rentenbarwerts ist von großer Bedeutung bei der Unternehmens- und Immobilienbewertung.
Was ist die ewige Rente?
Eine Rente ist ein wiederkehrender Zahlungsstrom. Die sogenannte „ewige Rente“ wird auf unbegrenzte Zeit ausbezahlt und verändert das Grundkapital nicht.
Die Berechnung des Rentenbarwerts einer ewigen Rente ist ein finanzmathematisches Werkzeug bei der Unternehmensbewertung und in der Frage, ob Immobilien vermietet oder verkauft werden sollen. In letzterem Fall muss der Wert der Immobilie mit den Mieteinnahmen (abzüglich Instandhaltungskosten und anderen Aufwendungen) verglichen werden.
Zeitwert des Geldes
Die Geldsumme zum heutigen Zeitpunkt ist mehr wert als dieselbe Summe in der Zukunft. Denn das Geld kann in der Zwischenzeit gewinnbringend angelegt werden („Zeitwert des Geldes“).
Die ewige Rente ist also eine Form der Investition, bei der das Kapital unberührt bleibt und in seinem Wert nicht verändert wird.
Arten der ewigen Rente
Folgende Arten der ewigen Rente sind denkbar:
- Ewige Rente: Die Rentenbeträge bleiben gleich
- Ewige Rente mit Wachstumsrate: Die Rente steigt jährlich an
- Fallende ewige Rente: Die Höhe der Rente verringert sich stetig
Berechnung der ewigen Rente
Der Endwert der ewigen Rente ist unendlich groß, da die Annahme besteht, die Rente habe keine zeitliche Begrenzung. Der Rentenbarwert gibt hingegen darüber Auskunft, welchen Wert eine Investition (Unternehmen, Immobilie) hat.
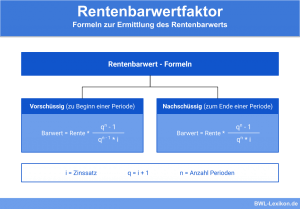
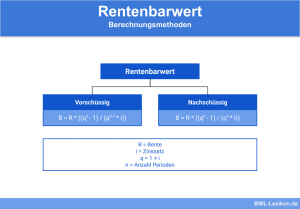
Größen zur Berechnung des Rentenbarwerts:
- B = Rentenbarwert der ewigen Rente
- z = Zinssatz in Dezimalform
- r = Rente je Periode
Formel: Rentenbarwert der ewigen Rente
![\[ Rentenbarwert~der~ewigen~Rente = \frac{Rente~je~Periode}{Zinssatz~in~Dezimalform} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-147d34f9b129d7abfe317deabed7f804_l3.png "Rendered by QuickLaTeX.com")
![\[ Rentenbarwert~der~ewigen~Rente = \frac{r}{z} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-f35be36ee8a8442ec426ba24f5c51ad8_l3.png "Rendered by QuickLaTeX.com")
![\[ Rentenbarwert~der~ewigen~Rente = \frac{25.000~Euro}{0,04} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-84de6c1956fd8c5c5c7020d3fc84d853_l3.png "Rendered by QuickLaTeX.com")
![\[ Rentenbarwert~der~ewigen~Rente = 625.000~Euro \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-f9b198521308aa18bf55ef834d314810_l3.png "Rendered by QuickLaTeX.com")
Der Barwert der Rente von 25.000 € jährlich beträgt 625.000 €.
Legt Herr X die 2 Millionen an, erhält er 100.000 € jährlich. Er sollte sich also für die Einmalzahlung entscheiden.
