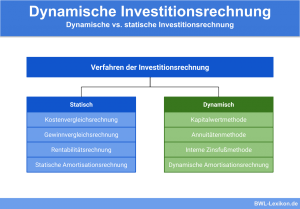
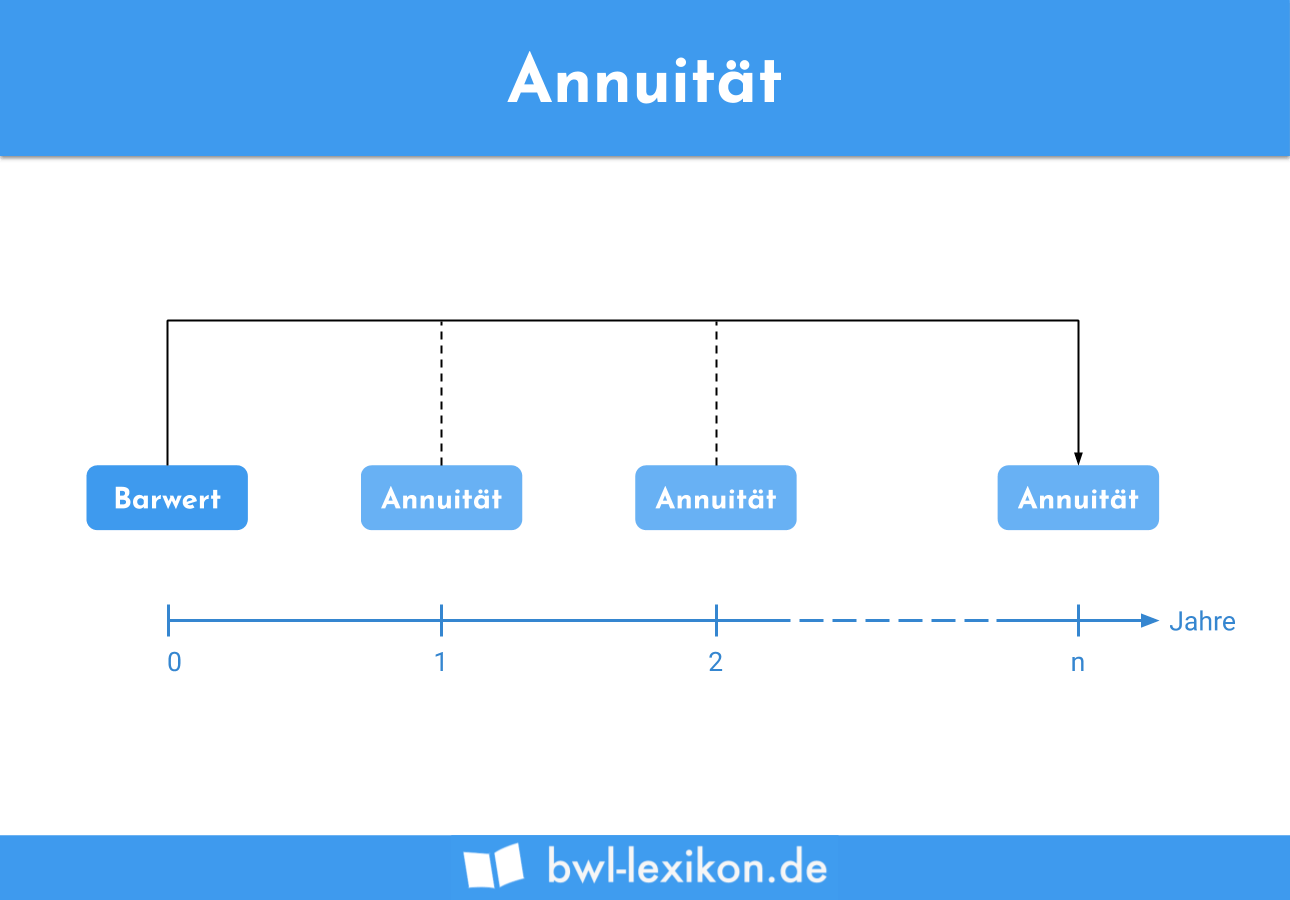
Unter Annuität versteht man die jährliche Rente, die eine Investition voraussichtlich abwerfen wird. Die Annuitäten bilden dabei den zu erwartenden Überschuss der Gewinne über die Ausgaben. Wie bei fast allen dynamischen Investitionsrechnungen wird auch bei der Annuitätenmethode der Zeitwert des Geldes, also der Zeitpunkt der Zahlungsströme, berücksichtigt. Abgeleitet wird dieses Rechenverfahren aus der Kapitalwertmethode.
In der folgenden Lektion erfährst du, welchen Wert der finanzmathematische Begriff der Annuität darstellt und wie dieser berechnet werden kann. Am Ende der Lektion findest du außerdem einige hilfreiche Übungsfragen zum Thema Annuität.
- Synonyme: jährliche Rente
- Englisch: annuity
Inhalt dieser Lektion
Warum ist die Annuität wichtig?
Durch die Annuitätenmethode kann der periodische Gewinn bzw. der Periodenüberschuss einer Investition ermittelt werden. Anhand dieser sogenannten Annuitäten können auf diese Weise verschiedene Investitionsprojekte gegeneinander abgewägt werden.
Was ist die Annuität ?
Die Annuität beschreibt jenen Wert, den eine Investition erwartungsgemäß pro Jahr abwirft. Sie wird anhand der Annuitätenmethode errechnet und ist eine durchschnittliche Größe, die sich über die gesamte Laufzeit der Investition nicht verändert.
Durch diese Art der Investitionsrechnung bekommt der potenzielle Investor einen Eindruck über die Vorteilhaftigkeit eines möglichen Projektes. Ausschlaggebend für das Ergebnis der Annuitätenmethode ist allerdings – wie bei der Kapitalwertmethode – die Höhe des Kalkulationszinssatzes.
Wie bei fast allen Verfahren der dynamischen Investitionsrechnung berücksichtigt die Annuitätenmethode den Zeitwert des Geldes, d. h. den Zeitpunkt der Zahlungsströme. So werden Zinsen und Zinseszinsen in die Berechnung der Annuität einbezogen.
Annuität richtig interpretieren
Mögliche Eigenschaften der Annuität:
- Die Annuität ist größer als 0: Von der Investition kann erwartet werden, dass sie jährliche Gewinne erwirtschaftet. Die Größe der Annuität beschreibt den jährlichen Überschuss der Einnahmen über die Ausgaben.
- Die Annuität ist gleich 0: Die getätigten Ausgaben (verzinst mit dem Kalkulationszinssatz) werden durch die Einnahmen wieder gedeckt, allerdings sind von der Investition keine jährlichen Gewinne zu erwarten.
- Die Annuität ist kleiner als 0: Von dem Investitionsprojekt ist abzusehen, da es keinen Überschuss erwirtschaften wird.
Wie wird die Annuität berechnet?
Für die Berechnung der Annuität ist der Annuitätenfaktor ausschlaggebend. Er ist der Kehrwert des Rentenbarwertfaktors und wird mit dem Ausgangsbetrag multipliziert. Der Annuitätenfaktor setzt sich aus Laufzeit der Investition und dem Kalkulationszinssatz zusammen.
Parameter der Annuitätenmethode:
- Af = Annuitätenfaktor
- z = Kalkulationszinssatz in Dezimalform
- t = Anzahl der Jahre der Laufzeit
Annuitätenfaktor berechnet (Formel)
![\[ Af = \frac{(1+z)^t*z}{(1+z)^t - 1} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-6c70ce3d9c2f52309a930dfb3dacef4d_l3.png "Rendered by QuickLaTeX.com")
![\[ Af = \frac{(1+0,035)^{10}*0,035}{(1+0,035)^{10} - 1} = 0,1202 \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-6888c4f67a1b9e2bd4dbcd3fe7f02bdb_l3.png "Rendered by QuickLaTeX.com")
Der Annuitätenfaktor beträgt also 0,1202.
Multipliziert wird er nun mit der Anfangssumme der Investition (1,5 Mio. €) = 180.361,51 €
Frau S kann also in den nächsten 10 Jahren jedes Jahr 180.361 € ihres Lottogewinns ausgeben, bis die gesamte Summe aufgebraucht ist.
