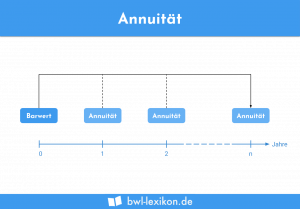
Annuitätenmethode

Enthält: Beispiele · Definition · Formeln · Grafiken · Übungsfragen

Die Annuitätenmethode ist eine klassische dynamische Investitionsrechenmethode und bildet ein Verbindungsstück zum Rentenbarwert. Anders als dieser wird hier allerdings nicht die Höhe der notwendigen Grundinvestition berechnet, sondern die Höhe der Zinsen oder der Rente pro Zeiteinheit. Diese Annuität – also eine regelmäßige Zahlung – ergibt die Höhe des Mehrbetrages pro Jahr (Periodenerfolg). Auch die Sinnhaftigkeit einer Investition kann durch die Anwendung der Annuitätenmethode evaluiert werden. Hier werden alle Zahlungen für die Investition über den gesamten Laufzeitraum verteilt.

In der folgenden Lektion erfährst du, wie die Annuität berechnet wird und welche Erkenntnisse daraus gezogen werden können. Am Ende der Lektion findest du außerdem einige hilfreiche Übungsaufgaben zum Thema Annuitätenmethode.

Englisch: annuity method

Warum ist die Annuitätenmethode wichtig?

Die Annuitätenmethode ist enorm hilfreich bei der Frage, wie hoch der Periodenerfolg, also der Zins oder die Rente je Zeiteinheit sein wird. Diese Art der dynamischen Investitionsrechenmethoden baut auf der Kapitalwertmethode auf und kann den Erfolg einer möglichen Investition vorhersagen.

Was ist die Annuitätenmethode?

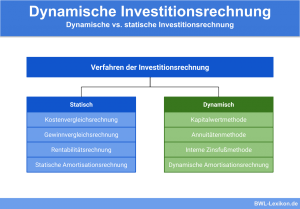
Die Annuitätenmethode ist eine der dynamischen Investitionsrechenmethoden und ist dem statischen Gewinnvergleich sehr ähnlich. Dabei werden die Überschüsse, Zinsen oder Renten einer Investition pro Periode errechnet. Wo der Gewinnvergleich den Gesamtgewinn einer Investition berechnet, stellt die Annuitätenmethode allerdings Periodengewinne fest. Es geht hier also um die gleichmäßige Höhe von wiederkehrenden Zahlungen über einen bestimmten Zeitraum hinweg.

Um die Höhe der jährlichen Rendite errechnen zu können, müssen folgende Parameter bekannt sein:

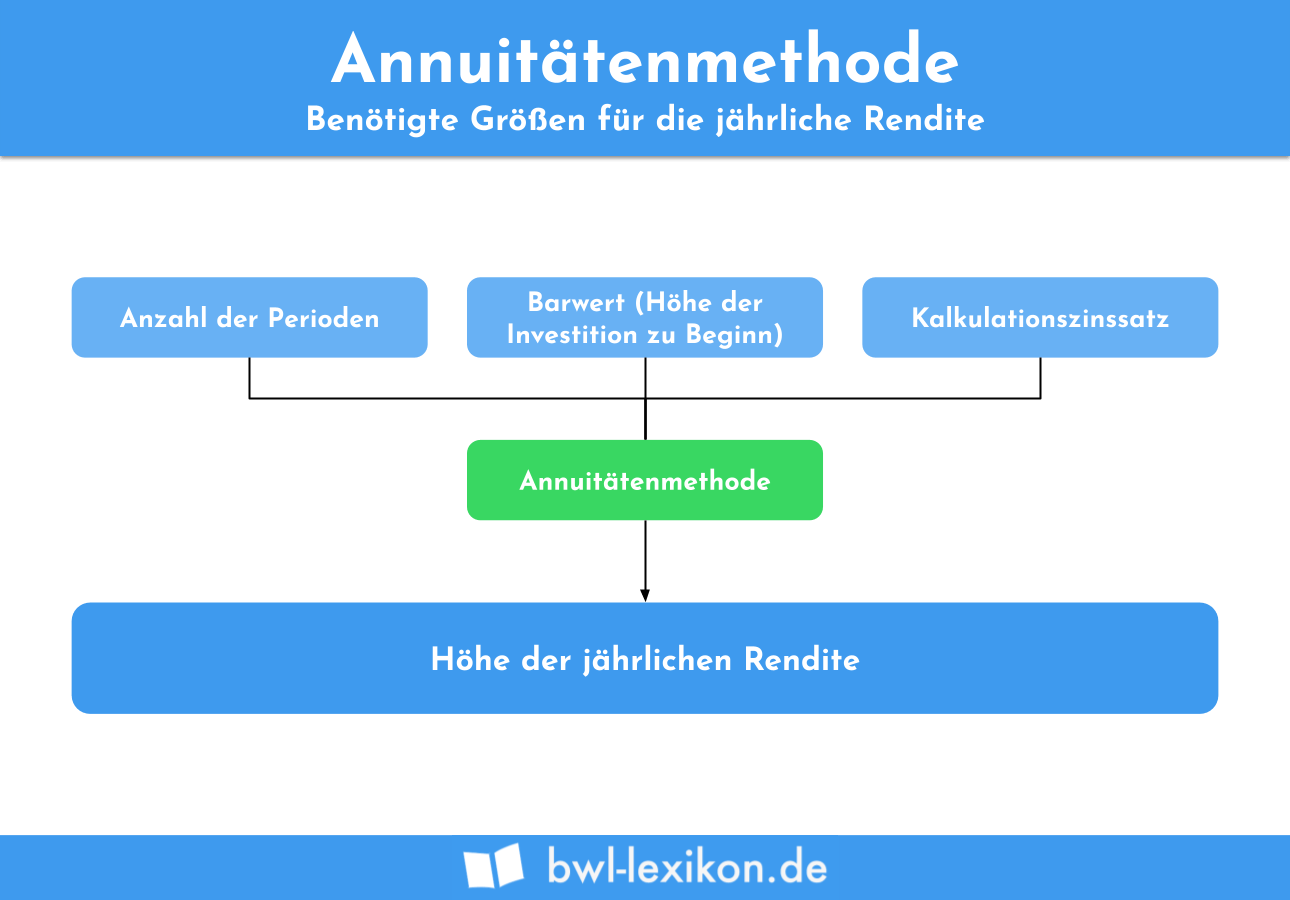
Annuitätenmethode: Benötigte Größen für die jährliche Rendite
Annuitätenmethode: Benötigte Größen für die jährliche Rendite

Der Begriff Annuität beschreibt dabei den Rückfluss an Vermögen, der jährlich ausgezahlt wird.

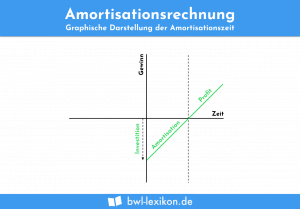
Die Annuitätenmethode ist allerdings auch eine Möglichkeit, die für eine Investition anfallenden Zahlungen auf den gesamten Zeitraum – unter Berücksichtigung der Annuität – aufzuteilen. Je kürzer dabei der Rückzahlungszeitraum, desto lohnender die Investition.

Berechnung der Annuität (Formel)

Die Annuität (g), also die Höhe der regelmäßigen Auszahlung, kann mithilfe der Annuitätenmethode errechnet werden, sofern der Barwert (K0) und der Kapitalwiedergewinnungsfaktor (KWF) bekannt sind. Der Kapitalgewinnungsfaktor wird auch Annuitätenfaktor genannt und ist der Kehrwert des Rentenbarwertfaktors.

Beide Werte werden multipliziert:

    \[ g = K_0 * \frac{i*(1+i)^n}{(1+i)^n-1}} \]

  • K0 = Nettobarwert
  • i = Zinssatz
  • n = Anzahl der Zeiteinheiten, (i. d. R. Jahre)

Vereinfacht ergibt sich:

    \[ g = K_0 * KWF \]

Annuität interpretieren

Ist g größer als 0, ist eine Investition stets als lohnend zu betrachten. Der Investor erhält die Investitionssumme bzw. sein eingesetztes Kapital wieder zurück und erhält darüber hinaus einen konstanten jährlichen Überschuss. Ist das Ergebnis der Rechnung kleiner als 0, sollte von einer eventuellen Investition Abstand genommen werden.

Annuität am Beispiel

Verrentung einer heutigen Zahlung berechnen

Um herauszufinden, wie hoch die Annuität bei einem bekannten Einstandswert K0 über einen festgelegten Zeitraum (n Jahre) bei einem bestimmten Zinssatz ist, kann die Annuitätenmethode genutzt werden.

Beispiel
Die Rentnerin Rita Rose möchte eine Summe von 150.000 € investieren und sich diese – inklusive einer 5-prozentigen Verzinsung – über die nächsten 10 Jahre auszahlen lassen. Mithilfe der Annuitätenmethode kann Frau Rose errechnen, über welchen Betrag sie jährlich verfügen kann.

Die zur Berechnung nötigen Parameter sind:

  • K0 = 150.000 Euro
  • i = 5 % (also 0,05)
  • n = 10 Jahre

Zunächst muss der Kapitalwiedergewinnungsfaktor berechnet werden:

    \[ g = K_0 * \sqrt{\frac{i*(1+i)^n}{(1+i)^n-1}} \]

    \[ KWF = \frac{0,081}{0,629} \]

    \[ KWF = 0,128 \]

Dann wird die Annuität berechnet:

    \[ Annuit\ddot{a}t = 150.000 * KWF \]

    \[ 150.000 * 0,128 = 19.200 \]

Frau Rose kann also 19.200 Euro jährlich als gleichbleibende Summe nutzen.

Verrentung einer späteren Zahlung berechnen

Auf der anderen Richtung kann auch ein gewünschter Endwert (Kn statt K0) zugrunde gelegt werden. Hier werden dann die jährlichen Beträge g berechnet, um festzustellen, ob der angenommene Zeitraum n realistisch ist. Dafür wird der Restwertverteilungsfaktor (RVF) genutzt.

Restwertverteilungsfaktor

Der Restwertverteilungsfaktor (auch Rückwärtsverteilungsfaktor) verteilt einen in n Jahren fälligen Betrag (Kn) gleichmäßig auf die Jahre und berücksichtigt dabei Zinsen und Zinseszinsen. Der RVF ist also zukunftsgerichtet.

    \[ Restwertverteilungsfaktor = \frac{i}{(1+i)^n-1} \]

Beispiel
Rita Rose hat noch keine 150.000 Euro. Sie möchte ihr Geld außerdem nicht für sich selbst anlegen, sondern nach zehn Jahren (n = 10) an ihre Enkelin auszahlen. Da sie insgesamt 150.000 Euro auszahlen möchte und ihre Bank 5,5 % Zinsen zahlen würde, will sie wissen, wie viel Geld sie jährlich anlegen muss.

Zur Berechnung benötigen wir:

  • Kn = 150.000 Euro
  • i = 5,5 % (also 0,055)
  • n = 10 Jahre

Zuerst berechnen wir den RVF, um diesen mit Kn zu multiplizieren.

    \[ Restwertverteilungsfaktor = \frac{i}{(1+i)^n-1} \]

    \[ Restwertverteilungsfaktor = \frac{0,055}{0,708} \]

    \[ Restwertverteilungsfaktor = 0,077 \]

Berechnung der Annuität:

    \[ Annuit\ddot{a}t = 150.000 * RVF = 150.000*0,077 = 11.550 \]

rau Rose müsste jährlich 11.550 Euro ansparen, um ihrer Enkelin nach zehn Jahren die gewünschten 150.000 Euro auszahlen zu kön

Übungsfragen

#1. Worum handelt es sich bei der Annuitätenmethode?

#2. Welcher Parameter muss zur Berechnung der Annuität stets gegeben sein?

#3. Womit wird der Kapitalwert multipliziert, um die Annuität berechnen zu können?

#4. Wann ist von einer Investition grundsätzlich eher abzusehen?

Fertig

Ergebnisse

Könnte dich auch interessieren:

Annuität

Annuität

Unter Annuität versteht man die jährliche Rente, die eine Investition voraussichtlich abwerfen wird. Die Annuitäten bilden dabei den zu erwartenden … weiterlesen >>

Abzinsungsfaktor: Aufzinsung vs. Abzinsung

Abzinsungsfaktor

Der Abzinsungsfaktor ist die ausschlaggebende Grundlage zur Berechnung des Anfangswertes einer Investition. Dieser Barwert errechnet sich mit den Parametern der … weiterlesen >>

Nichts passendes dabei?

Erkunde andere Fachbereiche oder benutze die Suchfunktion. Falls Du keine Antwort auf Deine Frage findest, schick uns gerne eine Nachricht, wir versuchen dann passenden Content für Dich zu schaffen.

Zur Übersicht
Oder lieber die Suche benutzen?