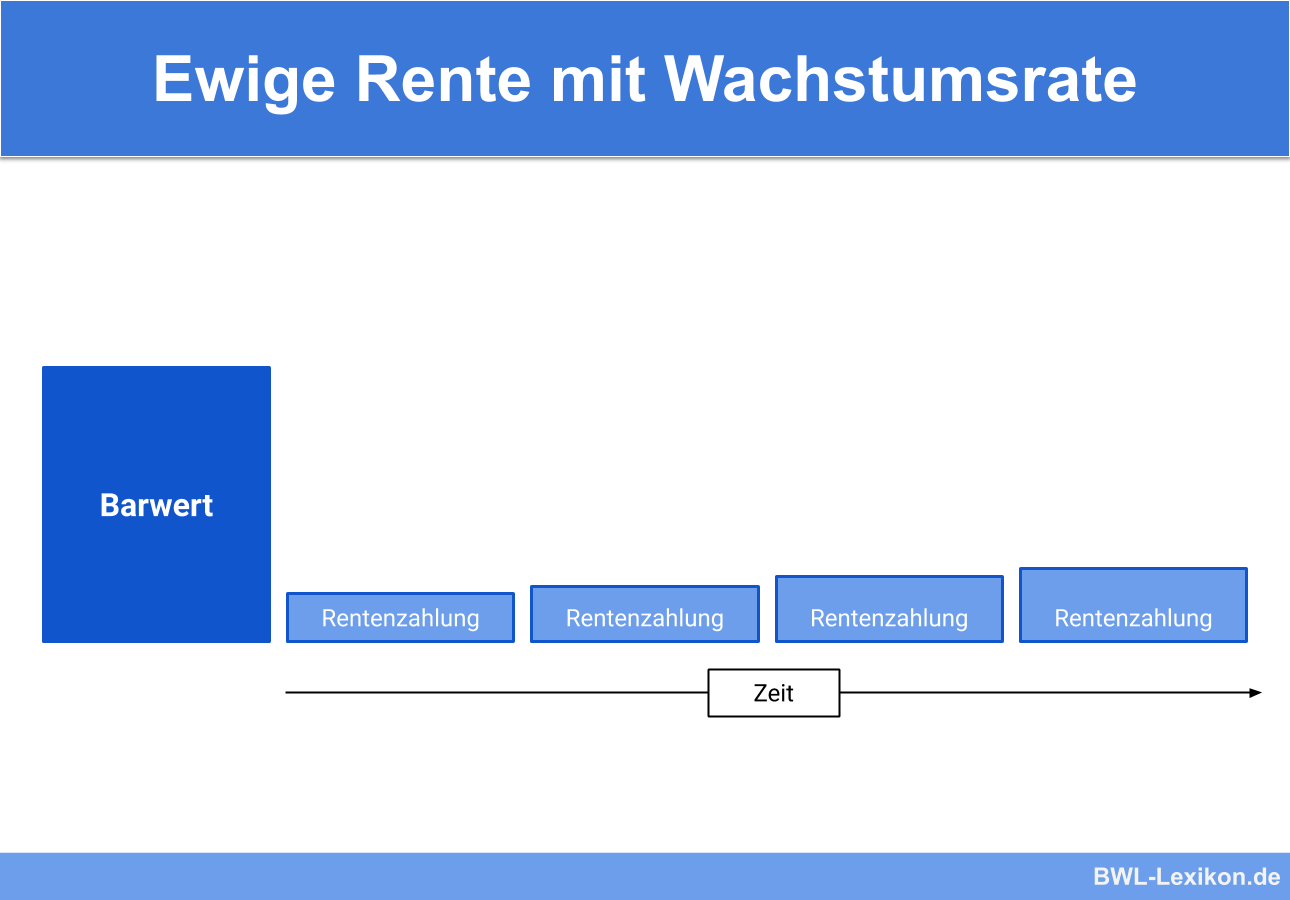
Die ewige Rente mit Wachstumsrate ist ein ständig wachsender Zahlungsstrom, der unbegrenzt verfügbar ist. Die Rentenentnahme ist unendlich lange möglich, da die Entnahmen am Stammkapital durch Gutschriften ausgeglichen werden. Die ewige Rente ist vor allem im Bereich der Unternehmensbewertung von Bedeutung, denn auch hier wird davon ausgegangen, dass der Betrieb auf unbestimmte Dauer bestehen bleibt.
In der folgenden Lektion erfährst du, was die ewige Rente mit Wachstumsrate ist und welche Relevanz sie in den Bereichen der Unternehmens- und Immobilienbewertung hat. Am Ende der Lektion findest du außerdem einige hilfreiche Übungsaufgaben zum Thema.
- Synonyme: Perpetuität mit Wachstumsrate
- Englisch: perpetual annuity with growth rate
Inhalt dieser Lektion
Warum ist die ewige Rente mit Wachstumsrate wichtig?
Die ewige Rente mit Wachstumsrate ist eine wichtige Größe bei der finanzmathematischen Bewertung eines Unternehmens oder einer Immobilie, obwohl sie in der Praxis nur sehr selten auftritt.
Was ist die ewige Rente mit Wachstumsrate?
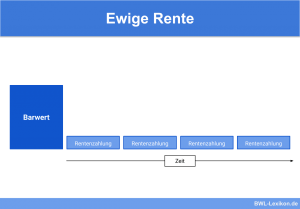
Die ewige Rente ist ein Begriff der Investitionsrechnung und beschreibt einen ständig wiederkehrenden Ertrag, der unendlich lange ausgeschüttet wird.
Spricht man von einer ‚ewigen Rente mit Wachstumsrate‘, wächst dieser Ertrag jährlich an. Damit ist der Endwert der ewigen Rente eine unendlich große Summe, der Barwert kann allerdings errechnet werden. Die ewige Rente verändert das Kapital der Investition bzw. des Unternehmens nicht.
Auch im Bereich der Immobilien spielt die ewige Rente eine wichtige Rolle: Die Entscheidung, ob ein Mietobjekt verkauft werden soll oder nicht, hängt im Wesentlichen von den wiederkehrend anfallenden Mieteinnahmen ab.
Berechnung der ewigen Rente mit Wachstumsrate
Die Wachstumsrate der ewigen Rente wird üblicherweise auch als Wachstumsabschlag bezeichnet, da er während des Rechenvorganges vom verwendeten Kalkulationszinssatz abgezogen wird. Dieser Abschlag ist also untrennbar mit dem Zinssatz verbunden und beeinflusst die ewige Rente direkt.
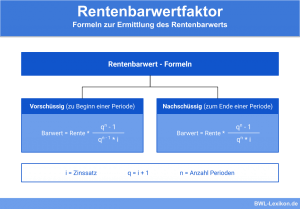
Formel für eine nachschüssige Rentenzahlung
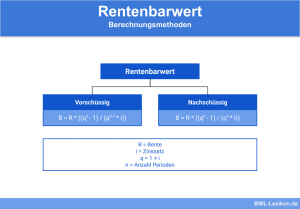
Der Zielwert der Berechnung ist der Barwert, der den Vergleichswert für die ewige Rente bildet. Zu unterscheiden ist ebenfalls zwischen vorschüssiger (wird am Anfang jeder Periode gezahlt) und nachschüssiger Rente (wird am Ende jeder Periode gezahlt).
Parameter zur Berechnung der ewigen Rente mit Wachstumsabschlag:
- R = Rentenbarwert
- A = Rente je Periode
- z = Kalkulationszinssatz in Dezimalform
- w = Wachstumsrate bzw. Wachstumsabschlag in Dezimalform
![\[ Rentenbarwert = \frac{A}{(z-w)} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-489424aec24893aa11aa856e6f25edb1_l3.png "Rendered by QuickLaTeX.com")
![\[ Rentenbarwert = \frac{150.000}{(0,04-0,03)} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-f96e413b463701b9469bc56a641017eb_l3.png "Rendered by QuickLaTeX.com")
![\[ Rentenbarwert = 15.000.000~Euro \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-b99e6b6c18b2d6fa8427e01a27613780_l3.png "Rendered by QuickLaTeX.com")
Der Barwert der ewigen Rente mit Wachstumsabschlag beträgt 15.000.000 €.
