▷ Arithmetisch degressive Abschreibung » Definition, Erklärung & Beispiele + Übungsfragen

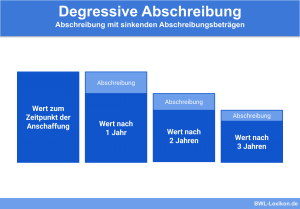
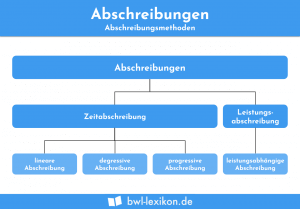
Bei der arithmetisch-degressiven Abschreibung (AfA) sinken die jährlichen Abschreibungen von Jahr zu Jahr um einen konstanten Betrag. Im Gegensatz zur geometrisch-degressiven Methode ist auf diese Weise eine vollständige Abschreibung ohne Restwert möglich.

In dieser Lektion lernst du, inwiefern die arithmetisch-degressive Abschreibung für das externe und interne Rechnungswesen relevant ist und wie du die Abschreibungsbeträge berechnest. Zum Schluss stellen wir dir noch einige Übungsaufgaben zur Lernkontrolle zur Verfügung.

Inhalt dieser Lektion

Anwendung der arithmetisch-degressiven Abschreibung

Für das externe Rechnungswesen hat die arithmetisch-degressive Abschreibung nur eingeschränkt Bedeutung, denn das Steuerrecht sieht diese Methode nicht vor. Bei der Erstellung des handelsrechtlichen Jahresabschlusses kann sie jedoch zur Anwendung kommen. Das führt zu Unterschieden zwischen Handels- und Steuerbilanz.

Im internen Rechnungswesen gibt es keine Beschränkungen, was die Wahl der Methode angeht. Es geht es primär um die verursachungsgerechte Erfassung der Abnutzung als Kosten. Hier eignet sich die arithmetisch-degressive Abschreibung für Wirtschaftsgüter, bei denen man von einem im Zeitverlauf gleichmäßig abnehmenden Wertverlust ausgehen kann.

Aufstellung des Abschreibungsplans

Bei der arithmetisch-degressiven Abschreibung sinken die Jahresabschreibungen kontinuierlich um einen gleichbleibenden Degressionsbetrag. Wenn dieser mit der Abschreibung im letzten Jahr übereinstimmt, spricht man auch von digitaler Abschreibung.

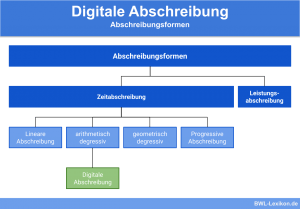
Die ‘digitale Abschreibung’ ist die häufigste Form der arithmetisch-degressiven Methode, weshalb sich die folgenden Ausführungen darauf beziehen. Das bedeutet, der Degressionsbetrag wird nicht willkürlich festgelegt, sondern anhand der Nutzungsdauer und der Abschreibungsgrundlage berechnet.

Die Aufstellung des Abschreibungsplans erfordert daher folgende Schritte:

Berechnung des Degressionsbetrags
Bestimmung der Abschreibungsbeträge
Ermittlung der Restwerte

Berechnung des Degressionsbetrags

Der Degressionsbetrag errechnet sich wie folgt:

$Degressionsbetrag = \frac{Abschreibungsgrundlage}{Summe~der~Nutzungsjahre}$

Beispiel

Ein Wirtschaftsgut mit Anschaffungskosten von 4.500 € soll über 5 Jahre hinweg abgeschrieben werden.

Der Degressionsbetrag wird folgendermaßen berechnet:

$Degressionsbetrag = \frac{4.500~Euro}{(1 + 2 + 3 + 4 + 5)} = 300~Euro$

Für die bilanzielle Abschreibung im externen Rechnungswesen legt man dabei die Anschaffungs- oder Herstellungskosten zugrunde und schreibt vollständig ab. Es gibt keinen Restwert. Die kalkulatorische Abschreibung im internen Rechnungswesen geht von den Wiederbeschaffungskosten aus und es kann ein Restwert stehen bleiben. Bei der Berechnung muss dieser zuerst vom Wiederbeschaffungswert abgezogen werden.

Folgende Formel führt zum gleichen Ergebnis. Sie ist vor allem bei einer längeren Abschreibungsdauer einfacher anzuwenden:

Degressionsbetrag berechnen bei bilanzieller Abschreibung:

$Degressionsbetrag = \frac{2 * AHK}{n * (n+1)}$

Degressionsbetrag berechnen bei kalkulatorischer Abschreibung:

$Degressionsbetrag = \frac{2 * (WK - RW)}{n * (n+1)}$

Legende:

D: Degressionsbetrag
n: Anzahl der Nutzungsjahre
AHK: Anschaffungs- oder Herstellungskosten
WK: Wiederbeschaffungskosten
RW: Restwert im Jahr n

Beispiel: kalkulatorische Abschreibung

Ein Unternehmen kauft eine Maschine, die 5 Jahre genutzt werden soll und danach voraussichtlich noch für 500 € verkauft werden kann. Nach dem Ausscheiden aus dem Unternehmen ist Ersatz notwendig, wofür 5.000 € eingeplant werden.

$Degressionsbetrag = \frac{2 * (5.000~Euro - 500~Euro)}{5} * (5+1) = 300~Euro$

Bestimmung der Abschreibungsbeträge

Der Abschreibungsbetrag für das erste Jahr ergibt sich durch Multiplikation des Degressionsbetrags mit der Nutzungsdauer. Für die folgenden Jahre wird jeweils der Degressionsbetrag von der Abschreibung des vorhergehenden Jahres abgezogen.

Alternativ kann man die Abschreibung für ein bestimmtes Jahr auch nach folgender Formel berechnen:

$Abschreibung = (Nutzungsdauer - Jahr + 1) * Degressionsbetrag$

Beispiel: Abschreibung berechnen

Ausgehend von der oben vorgestellten Situation mit 5 Jahren Nutzungsdauer und einem Degressionsbetrag von 300 € ergibt sich für das erste Jahr eine Abschreibung von 5 * 300 € = 1.500 €.

Durch fortlaufende Subtraktion des Degressionsbetrags erhält man die Abschreibungsbeträge der folgenden Jahre: 1.200 €, 900 €, 600 € und 300 €.

Bei alternativer Anwendung der genannten Formel erfolgt die Berechnung z. B. für das Jahr 3 auf diese Weise:

$Abschreibung = (5 - 3 + 1) * 300~Euro = 900~Euro$

Ermittlung der Restwerte

Den Abschreibungsbetrag für das erste Jahr zieht man vom Wiederbeschaffungswert bzw. von den Anschaffungs- oder Herstellungskosten ab, um den Restwert am Jahresende zu erhalten. Davon wird wiederum die Abschreibung des zweiten Jahres abgezogen usw..

Beispiel

Aus den oben genannten Beispielwerten ergibt sich folgender Abschreibungsplan:

Jahr	Abschreibung (€)	Restwert (€)
1	1.500	3.500
2	1.200	2.300
3	900	1.400
4	600	800
5	300	500

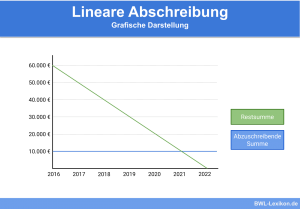
Am zugehörigen Diagramm wird sichtbar, dass die Abschreibungen im Zeitverlauf gleichmäßig, aber die Restwerte zu Beginn stärker abnehmen.

Arithmetisch degressive Abschreibung

Anwendung der arithmetisch-degressiven Abschreibung