Kalkulatorische Abschreibungen spielen nur für das interne Rechnungswesen eine Rolle, haben also keine Bedeutung für den Jahresabschluss. Ihre Aufgabe ist es, als Kostenbestandteile den Wertverzehr des Unternehmensvermögens so realistisch wie möglich abzubilden. Sie beeinflussen die Preisbildung und damit die Refinanzierung der Vermögensgegenstände über Produktverkäufe.
In dieser Lektion erfährst du, warum man zwischen kalkulatorischer und bilanzieller Abschreibung differenziert und wo die konkreten Unterschiede liegen. Außerdem lernst du die Berechnung der Abschreibungsbeträge mit verschiedenen Methoden kennen. Teste dein Wissen zum Schluss anhand einiger Übungsfragen.
Warum sind kalkulatorische Abschreibungen wichtig?
Kalkulatorische Abschreibungen gehen in die Kostenrechnung ein und haben somit nur Bedeutung für das interne Rechnungswesen. Sie unterscheiden sich von den im externen Rechnungswesen als Aufwand verbuchten bilanziellen Abschreibungen, die den Jahresabschluss und die Besteuerung beeinflussen.
Zweck der kalkulatorischen Abschreibungen
Zweck der kalkulatorischen Abschreibungen ist eine Kostenrechnung, die den Wertverzehr des Unternehmensvermögens verursachungsgerecht darstellt. Das ermöglicht realistische Wirtschaftlichkeitsbewertungen und eine Preisgestaltung, die notwendige Neuanschaffungen und damit den Substanzerhalt erlaubt.
Theoretisch könnte man der Kostenrechnung zwar auch die bilanziellen Abschreibungen zugrunde legen. Bei diesen steht jedoch die Verteilung der Anschaffungs- oder Herstellungskosten auf mehrere Wirtschaftsjahre nach handels- und steuerrechtlichen Vorschriften im Vordergrund. Kalkulatorische Abschreibungen sind nicht an diese Vorgaben gebunden, weshalb sich der Substanzverzehr damit realistischer abbilden lässt.
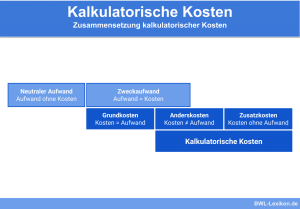
Die kalkulatorischen Abschreibungen gelten als Anderskosten. Das bedeutet, sie werden als Kosten in anderer Höhe erfasst als der entsprechende Aufwand im externen Rechnungswesen, also die bilanziellen Abschreibungen. Daneben gibt es auch kalkulatorische Zusatzkosten, denen kein Aufwand gegenübersteht, z. B. die kalkulatorischen Zinsen auf das Eigenkapital oder den kalkulatorischen Unternehmerlohn.
Unterschiede zwischen kalkulatorischen und bilanziellen Abschreibungen
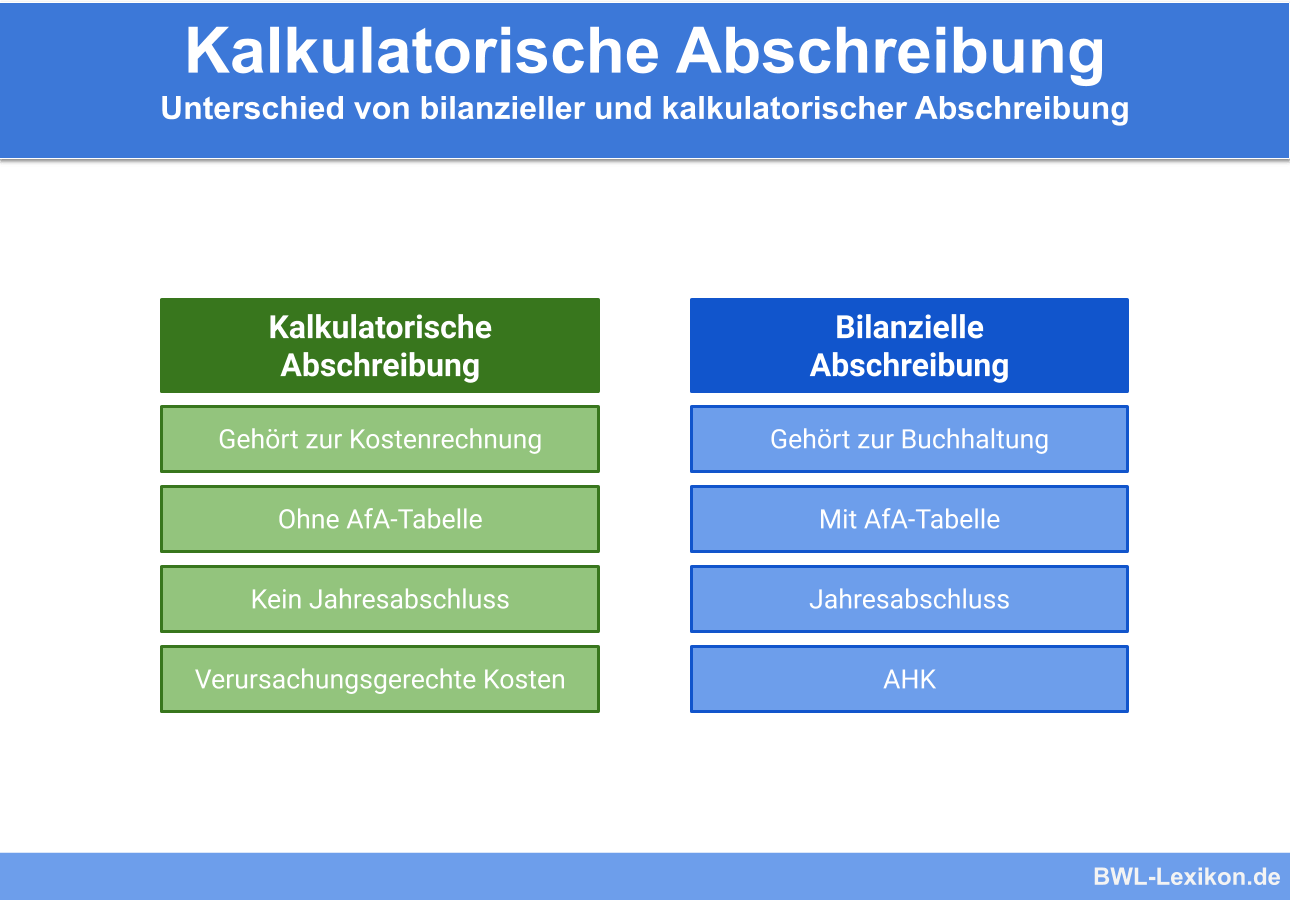
Warum es notwendig ist, kalkulatorische Abschreibungen zu bilden, wird deutlich, wenn man die konkreten Unterschiede zu den bilanziellen Abschreibungen betrachtet.
Folgende Tabelle stellt beide Varianten gegenüber:
| Kalkulatorische Abschreibungen | Bilanzielle Abschreibungen | |
|---|---|---|
| Zuordnung | internes Rechnungswesen | externes Rechnungswesen |
| Auswirkung auf den Jahresabschluss und die Besteuerung | nein | ja |
| Bindende gesetzliche Vorschriften | nein | ja |
| Anwendung von Sonderregelungen (z. B. Abschreibungsvereinfachungen oder Sonderabschreibungen) | nein | möglich |
| Zweck | verursachungsgerechte Bewertung des Substanzverzehrs | Verteilung der Anschaffungs- oder Herstellungskosten auf die Nutzungsdauer |
| Ausgangswert | Wiederbeschaffungswert zum Zeitpunkt des Ersatzes | Anschaffungs- oder Herstellungskosten |
| Abschreibungsdauer | orientiert sich an Erfahrungswerten | richtet sich meist nach offiziellen AfA-Tabellen |
| Abschreibungsverfahren | frei wählbar (möglichst verursachungsgerecht) | enge gesetzliche Vorgaben |
| Restwert | Schrottwert kann übrig bleiben | vollständige Abschreibung bzw. Erinnerungswert von 1 € |
Berechnung der kalkulatorischen Abschreibungen
Für die Berechnung der kalkulatorischen Abschreibungen müssen einige der Ausgangsgrößen erst ermittelt werden. Deshalb sind die im Folgenden vorgestellten Schritte erforderlich.
Abschreibungszeitraum schätzen
Der Abschreibungszeitraum soll der realen Nutzungsdauer des Vermögensgegenstandes im Unternehmen entsprechen. Auch wenn dieser bilanziell bereits voll abgeschrieben ist, kann die kalkulatorische Abschreibung noch weiter fortgeführt werden.
Wie lange das Wirtschaftsgut im Unternehmen genutzt werden kann, muss auf der Grundlage von Erfahrungen abgeschätzt werden. Die offiziellen AfA-Tabellen können natürlich als Orientierung dienen. Sollte sich die Einschätzung später als fehlerhaft erweisen oder unvorhersehbare Ereignisse zum schnelleren Verschleiß führen, ist der Abschreibungszeitraum zu korrigieren.
Wiederbeschaffungswert ermitteln
Während den bilanziellen Abschreibungen die Anschaffungs- oder Herstellungskosten zugrunde gelegt werden, gehen die kalkulatorischen Abschreibungen vom Wiederbeschaffungswert zum Ersatzzeitpunkt aus. Wenn z. B. eine Maschine vollständig kalkulatorisch abgeschrieben wurde, muss sie durch eine neue ersetzt werden.
Der Wiederbeschaffungswert ist im Normalfall höher als die Anschaffungs- oder Herstellungskosten, da es durch die Inflation und zum Teil auch durch technische Neuerungen zu Preissteigerungen kommt. Er kann mitunter auf der Grundlage von Erfahrungswerten geschätzt werden.
Ermittlung des Wiederbeschaffungswertes
Wenn man bei der Ermittlung des Wiederbeschaffungswertes nur die Preissteigerung durch Inflation zugrunde legt, gilt folgende Formel:
![\[ Wiederbeschaffungswert = Anschaffungskosten * (1 + durchschnittliche~Inflation~der~letzten~Jahre)^{Nutzungsjahre} \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-b7bf39888cd003d82b909aee6440e446_l3.png "Rendered by QuickLaTeX.com")
![\[ Wiederbeschaffungswert = 20.000~Euro * (1 + 0,014)^{10} = 22.983~Euro \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-7ef1ea4cd5ad546f87068bcc46dfd277_l3.png "Rendered by QuickLaTeX.com")
Endwert festlegen
Eine vollständige kalkulatorische Abschreibung mit dem Endwert 0 ist realistisch, wenn der Vermögensgegenstand nach dem Ausscheiden aus dem Unternehmen nicht mehr verkauft werden kann. Für bestimmten Wirtschaftsgüter lässt sich aber nach dem Ende der Nutzungsdauer noch ein Schrottwert erzielen. Dieser muss vor dem Berechnen der Abschreibungsbeträge vom Wiederbeschaffungswert abgezogen werden.
Abschreibungsbeträge berechnen
Für die kalkulatorische Abschreibung gibt es keine gesetzlichen Beschränkungen, was die Wahl der Abschreibungsmethode angeht. Wichtig ist, dass verursachungsgerecht abgeschrieben wird, weshalb immer die individuellen Gegebenheiten zu prüfen sind.
Es gibt folgende Möglichkeiten:
- linear
- leistungsabhängig
- arithmetisch degressiv
- geometrisch degressiv
- arithmetisch progressiv
- geometrisch progressiv
Für Fahrzeuge mit unregelmäßiger Nutzung bietet sich beispielsweise die Leistungsabschreibung an. Wenn eine Maschine zu Beginn ihrer Nutzungsdauer am stärksten verschleißt, empfiehlt sich die degressive Abschreibung. Progressiv kann hingegen abgeschrieben werden, wenn sich der Substanzverzehr im Lauf der Zeit intensiviert.
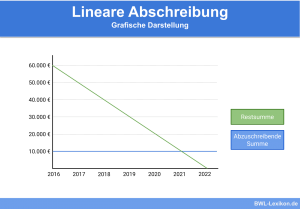
Lineare Abschreibung
Der linearen Abschreibung liegt die Annahme einer gleichmäßigen Abnutzung zugrunde. Sie kommt am häufigsten zur Anwendung. Dabei wird der Wiederbeschaffungswert, gegebenenfalls reduziert um den Schrottwert, durch die Anzahl der Nutzungsjahre geteilt, um den jährlichen Abschreibungsbetrag zu ermitteln.
Der jährliche Abschreibungsbetrag ergibt sich aus:
![\[ \frac{(10.000~Euro - 200~Euro)}{10} = 980~Euro \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-7a12b1932b28ea8196af49d449d73c37_l3.png "Rendered by QuickLaTeX.com")
Leistungsabschreibung
Bei der Leistungsabschreibung steht die Nutzungsdauer nicht sicher fest. Dafür lässt sich aber die Anzahl der insgesamt möglichen Leistungseinheiten abschätzen. Eine weitere Voraussetzung ist, dass sich die Leistung messen lässt. Der Abschreibungsbetrag ist umso höher, je intensiver das Wirtschaftsgut im jeweiligen Jahr genutzt wurde.
Der Wiederbeschaffungswert liegt bei 5.000 €.
Das ergibt:
![\[ \frac{5.000~Euro}{25.000~Stunden} = 0,20~Euro/Stunde. \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-14cf8887242cf45ac7d5e2d69a0925b5_l3.png "Rendered by QuickLaTeX.com")
Ergebnis: Im betreffenden Wirtschaftsjahr lief die Maschine 1.500 Stunden. Der Abschreibungsbetrag liegt somit bei 1.500 Stunden * 0,20 €/Stunde = 300 €.
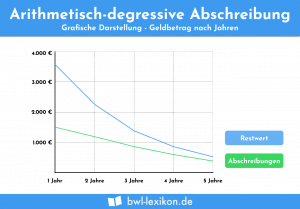
Arithmetisch-degressive Abschreibung
Bei der arithmetisch-degressiven Abschreibung sinkt der Abschreibungsbetrag jährlich um den gleichen Degressionsbetrag.
Der Degressionsbetrag ergibt sich aus:
![\[ \frac{45.000~Euro}{1+2+3+4+5} = 3.000~Euro \]](https://www.bwl-lexikon.de/app/ql-cache/quicklatex.com-4f6405babcda1d022feda524a8fd88b1_l3.png "Rendered by QuickLaTeX.com")
Daraus folgt dieser Abschreibungsplan:
| Jahr | Abschreibungsbetrag (€) | Restwert (€) |
|---|---|---|
| 1 | 15.000 | 30.000 |
| 2 | 12.000 | 18.000 |
| 3 | 9.000 | 9.000 |
| 4 | 6.000 | 3.000 |
| 5 | 3.000 | 0 |
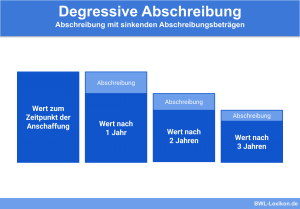
Geometrisch-degressive Abschreibung
Bei dieser Methode wird der Abschreibungsbetrag prozentual vom Restbuchwert berechnet. Dafür kommt jährlich der gleiche Prozentsatz zur Anwendung. Allerdings kann diese Methode nie einen Restwert von 0 € ergeben, weshalb früher oder später zur linearen Abschreibung gewechselt werden muss oder der restliche Betrag vollständig abzuschreiben ist.
Der Prozentsatz lässt sich aus dem Wiederbeschaffungswert, dem geplanten Restwert und der Nutzungsdauer berechnen. Wie das funktioniert, zeigt das folgende Beispiel.
Man teilt 3.000 € durch 20.000 € und zieht daraus die 5. Wurzel. Diesen Betrag zieht man von 1 ab und multipliziert das Ergebnis mit 100. Es ergibt sich ein Degressionssatz von 31,57 %.
Das ist der zugehörige Abschreibungsplan:
| Jahr | Abschreibungsbetrag (€) | Restwert (€) |
|---|---|---|
| 1 | 6.315 | 13.685 |
| 2 | 4.321 | 9.364 |
| 3 | 2.957 | 6.407 |
| 4 | 2.023 | 4.384 |
| 5 | 1.384 | 3.000 |
Progressive Abschreibung
Die progressive Abschreibung zeichnet sich dadurch aus, dass die Abschreibungsbeträge jährlich steigen. Man unterscheidet ebenfalls zwischen arithmetisch progressiver und geometrisch progressiver Abschreibung. Diese Methoden haben jedoch keine große praktische Bedeutung.
Übungsfragen
#1. Was ist der Sinn kalkulatorischer Abschreibungen?
#2. Muss die Ermittlung der kalkulatorischen Abschreibungen gesetzlichen Bestimmungen folgen?
#3. Zu welcher Kategorie gehören kalkulatorische Abschreibungen?
#4. Was hat für die Berechnung der kalkulatorischen Abschreibungsbeträge KEINE Bedeutung?
#5. Was ist die Berechnungsgrundlage für kalkulatorische Abschreibungen?
Ergebnisse
Sie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr Informationen
