Break Even Point

Enthält: Beispiele · Definition · Formeln · Grafiken · Übungsfragen

Der Break Even Point bezeichnet den Moment, an dem die Erlöse eines Produkts oder eines Unternehmens die Kosten ausgleichen. Das bedeutet, dass das Unternehmen an diesem Punkt weder Gewinn noch Verlust erwirtschaftet.

Wir zeigen dir in diesem Kapitel wann der Break Even Point eine Rolle spielt und wie er errechnet werden kann. Außerdem kannst du anhand unserer Übungsaufgaben dein Wissen rund um den Break Even Point auf die Probe stellen.

Synonyme: Gewinnschwelle | Nutzenschwelle

Warum ist der Break Even Point wichtig?

Die Ermittlung des Break Even Point dient der Beantwortung zweier wesentlicher unternehmerischer Fragen:

  • Wie viele Produkte müssen verkauft werden, um keinen Verlust zu machen?
  • Wie viel Umsatz muss mindestens generiert werden, um keinen Verlust zu machen?

Der Break Even Point ist daher eine wichtige Kennzahl zur Analyse und Steuerung eines Unternehmens. Kann die benötigte Stückzahl nicht verkauft werden, oder der Mindestumsatz nicht erzielt werden, müssen entsprechende Gegenmaßnahmen eingeleitet werden, um das Unternehmen vor einer möglichen Insolvenz zu bewahren.

Dies könnten beispielsweise sein:

  • Erhöhung der Vertriebs- oder Marketingaktivitäten
  • Kostensenkungsmaßnahmen
  • Herausnahme des betreffenden Produkts aus dem eigenen Sortiment

Kennt ein Unternehmen den Break Even Point, so kann es auch frühzeitig erkennen, wie viel Rückgang des Absatzes verkraftet werden kann. So kann das Unternehmen schnell auf Fehlentwicklungen reagieren und entsprechende Maßnahmen ergreifen.

Was ist der Break Even Point? Definition & Erklärung

Unternehmen können wirtschaftlich nur überleben und wachsen, wenn die unternehmerische Tätigkeit Gewinn erwirtschaftet. Der Unternehmensgewinn, auch ‘Überschuss’ genannt, ergibt sich aus der positiven Differenz von Kosten und Umsatz. Ist diese Differenz negativ, also sind die Kosten höher als der Umsatz, so spricht man von Verlust oder negativem Überschuss.

Der Punkt, an dem die Umsatzerlöse die Kosten ausgleichen, wird Break Even Point genannt. Er bezeichnet die Schwelle zur Gewinnzone, weshalb der Break Even Point auch als ‘Gewinnschwelle’ bezeichnet werden kann.

Die Ermittlung des Break Even Points spielt vor allem in zwei Fällen eine Rolle:

  • bei der Ermittlung der Gewinnschwelle eines gesamten Unternehmens, beispielsweise im Zuge einer Neugründung (Mehr-Produkt-Betrachtung)
  • bei der Ermittlung der Gewinnschwelle eines Produktes, beispielsweise bei einer Neu-Einführung auf dem Markt (Ein-Produkt-Betrachtung)

In der Ein-Produkt-Betrachtung wird der Break Even Point als Stückzahl ausgewiesen, während im Zuge der Mehr-Produkt-Betrachtung die Ausweisung des Gesamtumsatzes als relevant gilt.

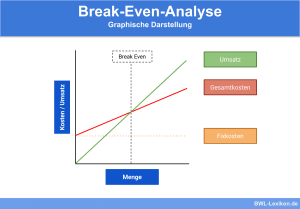
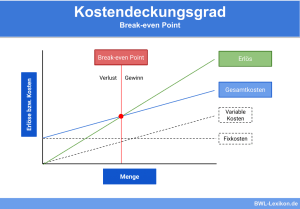
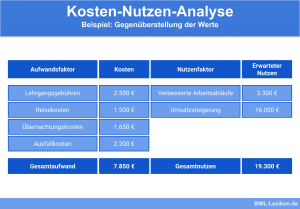
Grafische Darstellung des Break Even Point

Grafisch kann der Break Even Point bestimmt werden, in dem der Schnittpunkt der Umsatzkurve mit der Gesamtkostenkurve ermittelt wird.

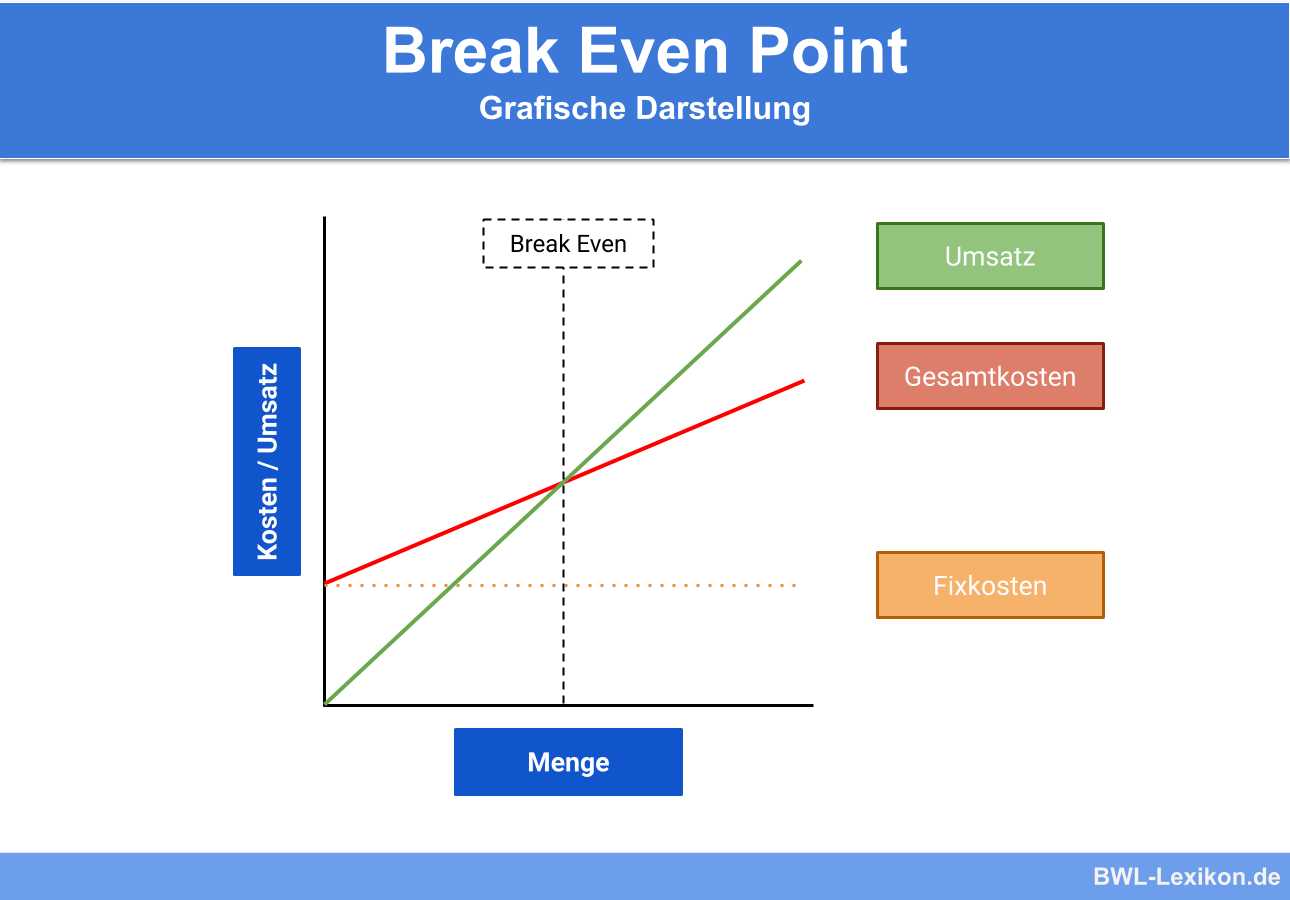
Break Even Point
Break Even Point

Ermittlung des Break Even Points in der Ein-Produkt-Betrachtung

Zur Ermittlung des Break Even Points werden zwei Größen benötigt:

Die gesamten variablen Kosten der Produktion geteilt durch die Menge der produzierten Produkte ergeben die variablen Stückkosten:

    \[ variable~St\ddot{u}ckkosten = \frac{gesamte~variable~Kosten}{produzierte~Menge} \]

Die variablen Stückkosten bilden die absolute Preisuntergrenze für ein Produkt. Das bedeutet, dass das Produkt nicht für einen geringeren Preis angeboten werden darf, da sonst mit jeder verkauften Einheit Verlust erwirtschaftet wird.

Die Gesamtkosten ergeben sich aus der Summe von variablen und fixen Kosten:

    \[ Gesamtkosten = variable~Kosten + fixe~Kosten \]

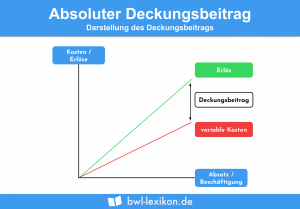
Zieht man die variablen Stückkosten vom Umsatzerlös eines Produkts ab, erhält man den Deckungsbeitrag eines Stücks:

    \[ Deckungsbeitrag~pro~St\ddot{u}ck = Umsatzerl\ddot{o}s~eines~Produkts - variable~St\ddot{u}ckkosten \]

Um den Deckungsbeitrag eines Produkts für das Unternehmen zu berechnen, multipliziert man in dieser Formel die variablen Stückkosten mit der Stückanzahl:

    \[ Deckungsbeitrag = Umsatzerl\ddot{o}s - variable~St\ddot{u}ckkosten * St\ddot{u}ckzahl \]

Der Deckungsbeitrag gibt an, wieviel das Produkt zur Deckung der Fixkosten des Unternehmens beiträgt.

Hat man diese Größen ermittelt, kann man daraus die Gewinnschwelle errechnen.

Für den Break Even Point gilt:

    \[ Gesamtumsatz - Gesamtkosten = 0 \]

Der Gesamtumsatz ergibt sich folgendermaßen:

    \[ Gesamtumsatz = Einzelpreis * St\ddot{u}ckzahl \]

Die Gesamtkosten berechnen sich aus:

    \[ Gesamtkosten = (variable~Stückkosten * St\ddot{u}ckzahl) + fixe~Kosten \]

Für die Ermittlung der Gewinnschwelle gilt also:

    \[ 0 = (Einzelpreis * St\ddot{u}ckzahl) - (variable~St\ddot{u}ckkosten * St\ddot{u}ckzahl) + fixe~Kosten \]

Um die Stückzahl herauszufinden, an der der Break Even Point erreicht wird, werden die beiden Gleichungen gleichgesetzt und nach der Stückzahl aufgelöst:

Schritt 1:

    \[ (Einzelpreis * St\ddot{u}ckzahl) = (variable~St\ddot{u}ckkosten * St\ddot{u}ckzahl) + fixe~Kosten \]

Schritt 2:

    \[ St\ddot{u}ckzahl = \frac{fixe~Kosten}{Einzelpreis - variable~St\ddot{u}ckkosten} \]

Schritt 3:

    \[ St\ddot{u}ckzahl = \frac{fixe~Kosten}{Deckungsbeitrag~pro~St\ddot{u}ck} \]

Das gewonnene Ergebnis gibt also an, wieviel von dem Produkt mindestens verkauft werden muss, damit es die Gewinnschwelle erreicht.

Beispiel: Break Even Point ermitteln
Die ‘GuterHunger AG’ möchte eine neue Fertigsuppe auf dem Markt einführen. Hierzu soll die monatliche Gewinnschwelle errechnet werden.

Es gelten folgende Voraussetzungen:

  • Die monatlichen Fixkosten für die Produktion dieses Produkts betragen 1.000 €.
  • Die variablen Kosten pro Stück liegen bei 1,00 €.
  • Verkauft wird das Produkt für 3,00 €.

Der Deckungsbeitrag pro Fertigsuppe ergibt sich also folgendermaßen:

    \[ Deckungsbeitrag~pro~St\ddot{u}ck = Umsatzerl\ddot{o}s~pro~St\ddot{u}ck - variable~Kosten~pro~St\ddot{u}ck. \]

    \[ Deckungsbeitrag~pro~St\ddot{u}ck = 3,00~EUR - 1,00~EUR = 2,00~EUR \]

Zur Ermittlung der Gewinnschwelle gilt:

    \[ Break~Even~Point = \frac{Fixkosten}{Deckungsbeitrag~pro~St\ddot{u}ck} \]

    \[ Break~Even~Point = \frac{1.000~EUR}{2~EUR} = 500~St\ddot{u}ck \]

Das Unternehmen muss also pro Monat mindestens 500 Fertigsuppen verkaufen, damit es die Gewinnschwelle erreicht. Ab der 501 Fertigsuppe erwirtschaftet die ‘GuterHunger AG’ Gewinn mit dem Produkt.

Ermittlung des Break Even Points in der Mehr-Produkt-Betrachtung

Für Unternehmen, die mehr als ein Produkt verkaufen kommt die ‘Mehr-Produkt-Betrachtung’ des Break Even Points zum Zuge.

Der Break Even Point wird dabei als Mindestumsatz bezeichnet, der insgesamt erzielt werden muss, damit das Unternehmen keinen Verlust erwirtschaftet. Da sich die einzelnen Parameter, wie variable Kosten, Verkaufspreis und Stückzahl der einzelnen Gewinnschwellen unterscheiden wird dazu folgende Formel verwendet.

Formel:

    \[ U_{BEP} = \frac{fixe~Kosten}{(\frac{\sum_{j=n}^n(p_j-k_j)*x_j}{\sum_{j=1}^n * p_j * x_j})} = \frac{fixe~Kosten}{(\frac{\sum_{j=n}^n(db_j)*x_j}{\sum_{j=1}^n * p_j * x_j})} \]

  • UBEP: Mindestumsatz
  • n: Anzahl der Produkte
  • pj: Verkaufspreis des Produkts j
  • kj: variable Kosten von Produkt j
  • xj: Stückzahl von Produkt j
  • dbj: Deckungsbeitrag von Produkt j
Beispiel: Berechnung Break Even Point bei Mehr-Produkt-Betrachtung

Die ‘GuterHunger AG’ vertreibt neben der Fertigsuppe auch Tiefkühlpizza.

Folgende Werte sind bekannt:

Die Fixkosten des Unternehmens betragen 2.500 €.

Für die Tiefkühlpizza:

  • dbp = 2,50 €
  • xp = 800 Stück
  • pp = 3,50 €
Für die Fertigsuppe:

  • dbs = 2,00 €
  • xs = 500 Stück
  • ps = 3,00 €

Der Mindestumsatz beträgt also:

    \[ U_{BEP} = \frac{fixe~Kosten}{(\frac{db_p*x_p}{p_p * x_p}+\frac{db_s*x_s}{p_s*x_s})} = \frac{2.500 Euro}{(\frac{2,50~Euro*800~Stk.}{3,50~Euro*800~Stk.}+\frac{2,00~Euro * 500~Stk.}{3,00~Euro*500~Stk.})} = 7.309,01~Euro \]

Insgesamt muss die Guter Hunger AG also 7.309, 01 € Umsatz pro Monat erwirtschaften, um die Gewinnschwelle zu erreichen.

Übungsfragen

 

Ergebnisse

#1. Was ist der Break Even Point?

#2. Welche Vorteile bietet der Break Even Point?

#3. “Der Break Even Point ist eine wichtige Kennzahl zur Ermittlung der Rentabilität eines Unternehmens.” – diese Aussage ist:

#4. “Der Break Even Point kann anhand des Schnittpunkts der Gesamtkostenkurve und der Umsatzkurve ermittelt werden.” – Diese Aussage ist:

#5. “Die Ermittlung des Break Even Points kann sowohl für einzelne Produkte als auch für ganze Unternehmen mit mehreren Produkten durchgeführt werden.” – diese Aussage ist:

Vorherige
Fertig

Könnte dich auch interessieren:

Break-Even-Analyse

Break Even Analyse

Die Break-Even-Analyse dient der Berechnung der Gewinnschwelle eines eines neuen Produkts bzw. eines Unternehmens oder Unternehmensbereichs. Sie dient zur Ermittlung … weiterlesen >>

Pain Points: Typische Arten von Schmerzpunkten

Pain Points

Pain Points – zu Deutsch: Schmerzpunkte – ergeben sich, wenn ein Kunde feststellt, dass ein Produkt falsch konzipiert wurde, oder … weiterlesen >>

Kostendeckungsgrad: Break-Even Point

Kostendeckungsgrad

Der Kostendeckungsgrad ist eine betriebswirtschaftliche Kennzahl. Er liefert Informationen darüber, wie das Verhältnis der Gesamtkosten im Unternehmen zu seinen Umsatzerlösen … weiterlesen >>

Nichts passendes dabei?

Erkunde andere Fachbereiche oder benutze die Suchfunktion. Falls Du keine Antwort auf Deine Frage findest, schick uns gerne eine Nachricht, wir versuchen dann passenden Content für Dich zu schaffen.

Zur Übersicht
Oder lieber die Suche benutzen?